Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-08T22:16:16.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental sensitivity analysis of the global properties of a two-dimensional turbulent wake

Published online by Cambridge University Press:  16 January 2012

Vladimir Parezanović  and
Olivier Cadot
Vladimir Parezanović*
Affiliation:
Unité de Mécanique, École Nationale Supérieure de Techniques Avancées de ParisTech, Chemin de la Hunière, 91761 Palaiseau, France
Olivier Cadot
Affiliation:
Unité de Mécanique, École Nationale Supérieure de Techniques Avancées de ParisTech, Chemin de la Hunière, 91761 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

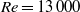The sensitivity of the global properties of a two-dimensional turbulent wake produced by the separated flow of a ‘D’-shaped cylinder at is investigated experimentally using a small circular control cylinder as a local disturbance. The height of the main cylinder is 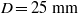and control cylinders are of diameters 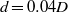and 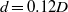, the former being smaller than the shear layer thickness detaching from the main cylinder, while the latter is larger. In both cases, the control cylinder is able to modify the global frequency, base pressure and spanwise velocity correlation. The results are presented as sensitivity maps. Reynolds stresses spatial structure and the recirculation bubble length are examined in detail when the control cylinder is displaced vertically across the wake at a fixed downstream location. It is found that the increase of the recirculation bubble length is accompanied by a damping of Reynolds stresses with a downstream shift of their spatial structures together with the base pressure increase. The global frequency can be either decreased or increased independently of the bubble length modification. The sensitivity of these global properties is interpreted on the basis of the ability of the control cylinder to change the size of the formation region of the Kármán vortex street by interacting with the primary detached shear layers. The corresponding physical mechanisms are discussed. The impact of a two-dimensional control cylinder on the three-dimensional properties of the wake is examined through spanwise correlation. This is found to be improved whenever the control cylinder is placed inside the recirculation region of the main cylinder wake.

JFM classification

Instability: Absolute/convective instability Flow Control: Flow Control Wakes/Jets: Separated flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 693 , 25 February 2012 , pp. 115 - 149
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Apelt, C. J. & West, G. S. 1975 The effects of wake splitter plates on bluff-body flow in the range . Part 2. J. Fluid Mech. 71, 145–160.CrossRefGoogle Scholar
2. Apelt, C. J., West, G. S. & Szewczyk, A. A. 1973 The effects of wake splitter plates on the flow past a circular cylinder in the range . J. Fluid Mech. 61, 187–198.CrossRefGoogle Scholar
3. Bearman, P. W. 1965 Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 21, 241–255.CrossRefGoogle Scholar
4. Bloor, M. S. 1964 The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 19, 290–304.CrossRefGoogle Scholar
5. Cadot, O., Thiria, B. & Beaudoin, J.-F. 2009 Passive drag control of a turbulent wake by local disturbances. In Unsteady Separated Flows and their Control (ed. Braza, M. & Hourigan, K. ), pp. 529–537. Springer.CrossRefGoogle Scholar
6. Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
7. Couairon, A. & Chomaz, J. M. 1999 Fully nonlinear global modes in slowly varying flows. Phys. Fluids 11 (12), 3688–3703.CrossRefGoogle Scholar
8. Crouch, J. D., Garbaruk, A., Magidov, D. & Travin, A. 2009 Origin of transonic buffet on aerofoils. J. Fluid Mech. 628, 357–369.CrossRefGoogle Scholar
9. Dalton, C., Xu, Y. & Owen, J. C. 2001 The suppression of lift on a circular cylinder due to vortex shedding at moderate Reynolds numbers. J. Fluids Struct. 15, 617–628.CrossRefGoogle Scholar
10. Franc, J.-P. & Michel, J.-M. 2005 Fundamentals of Cavitation. Springer.CrossRefGoogle Scholar
11. Gerrard, J. H. 1966 The mechanics of the formation region of vortices behind bluff bodies. J. Fluid Mech. 25, 401–413.CrossRefGoogle Scholar
12. Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
13. Goujon-Durand, S., Jenffer, P. & Wesfreid, J. E. 1994 Downstream evolution of the Bénard–von Kármán instability. Phys. Rev. E 50 (1), 308–313.CrossRefGoogle ScholarPubMed
14. Hill, D. C. 1992 A theoretical approach for analysing the restabilization of wakes. NASA Tech. Rep. 92, 29394.Google Scholar
15. Kuo, C.-H., Chiou, L.-C. & Chen, C.-C. 2007 Wake flow pattern modified by small control cylinders at low Reynolds number. J. Fluids Struct. 23 (6), 938–956.CrossRefGoogle Scholar
16. Luchini, P., Giannetti, F. & Pralits, J. 2008 Structural sensitivity of linear and nonlinear global modes. In Proceedings of Fifth AIAA Theoretical Fluid Mechanics Conference, Seattle, Washington, AIAA Paper 2008-4227.Google Scholar
17. Luchini, P., Giannetti, F. & Pralits, J. 2009 Structural sensitivity of the finite-amplitude vortex shedding behind a circular cylinder. In Unsteady Separated Flows and their Control (ed. Braza, M. & Hourigan, K. ), pp. 151–160. Springer.CrossRefGoogle Scholar
18. Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
19. Mittal, S. 2001 Control of flow past bluff bodies using rotating control cylinders. J. Fluids Struct. 15, 291–326.CrossRefGoogle Scholar
20. Mittal, S. & Raghuvanshi, A. 2001 Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. Intl J. Numer. Meth. Fluids 35, 421–447.3.0.CO;2-M>CrossRefGoogle Scholar
21. Norberg, C. 2001 Flow around a circular cylinder: aspects of fluctuating lift. J. Fluids Struct. 15, 459–469.CrossRefGoogle Scholar
22. Parezanović, V. 2011 Experimental study of the sensitivity of global properties of turbulent bluff body wakes using steady disturbance methods. PhD thesis, Ecole Nationale Superiéure de Techniques Avancées de ParisTech.Google Scholar
23. Parezanović, V. & Cadot, O. 2009a The impact of a local perturbation on global properties of a turbulent wake. Phys. Fluids 21 (7), 071701.CrossRefGoogle Scholar
24. Parezanović, V. & Cadot, O. 2009b Modulated global mode of a controlled wake. In Advances in Turbulence XII (ed. Eckhardt, B. ), pp. 217–220. Springer.CrossRefGoogle Scholar
25. Pastoor, M., Henning, L., Noack, B. R., King, R. & Tadmor, G. 2008 Feedback shear layer control for bluff body drag reduction. J. Fluid Mech. 608, 161–196.CrossRefGoogle Scholar
26. Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
27. Prasad, A. & Williamson, C. H. K. 1997 Three-dimensional effects in turbulent bluff-body wakes. J. Fluid Mech. 343, 235–265.Google Scholar
28. Roshko, A. 1954. On the drag and shedding frequency of two-dimensional bluff bodies. NACA Tech. Note 3619.Google Scholar
29. Sakamoto, H. & Haniu, H. 1994 Optimum suppression of fluid forces acting on circular cylinder. Trans. ASME: J. Fluids Engng 113, 183–189.Google Scholar
30. Sakamoto, H., Haniu, H. & Tan, K. 1991 An optimum suppression of fluid forces by controlling a shear layer separated from a square prism. Trans. ASME: J. Fluids Engng 113, 183–189.Google Scholar
31. Strykowski, P. J. & Sreenivasan, K. R. 1985 The control of transitional flows. In AIAA Shear Flow Control Conference, Boulder, CO, March 12–14, 1985. American Institute of Aeronautics and Astronautics.Google Scholar
32. Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
33. Thiria, B., Cadot, O. & Beaudoin, J.-F. 2009 Passive drag control of a blunt trailing edge cylinder. J. Fluids Struct. 25, 766–776.CrossRefGoogle Scholar
34. Thiria, B., Goujon-Durand, S. & Wesfreid, J. E. 2006 The wake of a cylinder performing rotary oscillations. J. Fluid Mech. 560, 123–147.CrossRefGoogle Scholar
35. Thiria, B. & Wesfreid, J. E. 2007 Stability properties of forced wakes. J. Fluid Mech. 579, 137–161.CrossRefGoogle Scholar
36. Weber, R. & Hureau, J. 2001 Ideal fluid flow past obstacles in an arbitrary channel: comparison of numerical and experimental results. J. Fluid Mech. 447, 129–148.CrossRefGoogle Scholar
37. Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
38. Wu, T. Y. T. 1972 Cavity and wake flows. Annu. Rev. Fluid Mech. 4, 243–284.CrossRefGoogle Scholar
39. Yildirim, I., Rindt, C. C. M. & Steenhoven, A. A. 2010 Vortex dynamics in a wire-disturbed cylinder wake. Phys. Fluids 22 (9), 094101.CrossRefGoogle Scholar
40. Zielinska, B. J. A. & Wesfreid, J. E. 1995 On the spatial structure of global modes in wake flow. Phys. Fluids 7, 1418–1424.CrossRefGoogle Scholar