Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-01T04:03:16.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental particle paths and drift velocity in steep waves at finite water depth

Published online by Cambridge University Press:  25 November 2016

John Grue  and
Jostein Kolaas
John Grue*
Affiliation:
Mechanics Division, Department of Mathematics, University of Oslo, Oslo, Norway
Jostein Kolaas
Affiliation:
Mechanics Division, Department of Mathematics, University of Oslo, Oslo, Norway
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

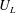The Lagrangian paths, horizontal Lagrangian drift velocity, $U_{L}$, and the Lagrangian excess period, 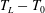$T_{L}-T_{0}$, where 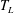$T_{L}$ is the Lagrangian period and 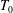$T_{0}$ the Eulerian linear period, are obtained by particle tracking velocimetry (PTV) in non-breaking periodic laboratory waves at a finite water depth of 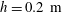$h=0.2~\text{m}$, wave height of 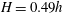$H=0.49h$ and wavenumber of 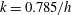$k=0.785/h$. Both 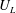$U_{L}$ and 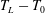$T_{L}-T_{0}$ are functions of the average vertical position of the paths, 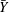$\bar{Y}$, where 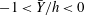$-1<\bar{Y}/h<0$. The functional relationships 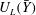$U_{L}(\bar{Y})$ and 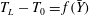$T_{L}-T_{0}=f(\bar{Y})$ are very similar. Comparisons to calculations by the inviscid strongly nonlinear Fenton method and the second-order theory show that the streaming velocities in the boundary layers below the wave surface and above the fluid bottom contribute to a strongly enhanced forward drift velocity and excess period. The experimental drift velocity shear becomes more than twice that obtained by the Fenton method, which again is approximately twice that of the second-order theory close to the surface. There is no mass flux of the periodic experimental waves and no pressure gradient. The results from a total number of 80 000 experimental particle paths in the different phases and vertical positions of the waves show a strong collapse. The particle paths are closed at the two vertical positions where 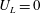$U_{L}=0$.

JFM classification

Geophysical and Geological Flows: Ocean processes Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 810 , 10 January 2017 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. G. & McIntyre, M. E. 1978 An exact theory of waves on a Lagrangian mean flow. J. Fluid Mech. 89, 609–646.Google Scholar
Ardhuin, F., Marié, L., Rascle, N., Forget, P. & Roland, A. 2009 Observation and estimation of Lagrangian, Stokes and Eulerian currents induced by wind and waves at the sea surface. J. Phys. Oceanogr. 39 (11), 2820–2838.Google Scholar
Bagnold, R. A. 1947 Sand movement by waves: some small-scale experiments with sand of very low density. J. Inst. Civil Engng 27 (4), 447–469.CrossRefGoogle Scholar
Constantin, A. 2006 The trajectories of particles in Stokes waves. Invent. Math. 166, 523–535.CrossRefGoogle Scholar
Constantin, A. 2015 The flow beneath a periodic travelling surface water wave. J. Phys. A 48, 143001.CrossRefGoogle Scholar
Dalziel, S. B. 1992 Decay of rotating turbulence: some particle tracking experiments. Appl. Sci. Res. 49, 217–244.Google Scholar
Fenton, J. D. 1988 The numerical solution of steady water wave problems. Comput. Geosci. 14 (3), 357–368.CrossRefGoogle Scholar
Gjøsund, S. H. 2003 A Lagrangian model for irregular waves and wave kinematics. J. Offshore Mech. Arctic Engng 125, 94–102.Google Scholar
Groeneweg, J. & Klopman, G. 1998 Changes of the mean velocity profiles in the combined wave–current motion described in a GLM formulation. J. Fluid Mech. 370, 271–296.CrossRefGoogle Scholar
Grue, J., Kolaas, J. & Jensen, A. 2014 Velocity fields in breaking-limited waves on finite depth. Eur. J. Mech. (B/Fluids) 47, 97–107.CrossRefGoogle Scholar
Hsu, H.-C., Chen, Y.-Y. & Wang, C.-F. 2010 Perturbation analysis of short-crested waves in Lagrangian coordinates. Nonlinear Anal. 11, 1522–1536.Google Scholar
Longuet-Higgins, M. S. 1953 Mass transport in water waves. Phil. Trans. R. Soc. Lond. A 245, 535–581.Google Scholar
Longuet-Higgins, M. S. 1960 Mass transport in the boundary layer at a free oscillating surface. J. Fluid Mech. 8, 293–306.Google Scholar
Longuet-Higgins, M. S. & Stewart, R. W. 1962 Radiation stress and mass transport in gravity waves, with applications to ‘surf beats’. J. Fluid Mech. 13, 481–504.Google Scholar
McIntyre, M. E. 1981 On the ‘wave momentum myth’. J. Fluid Mech. 106, 331–347.Google Scholar
Monismith, S. G., Cowen, E. A., Nepf, H. M., Magnaudet, J. & Thais, L. 2007 Laboratory observations of mean flows under surface gravity waves. J. Fluid Mech. 573, 131–147.Google Scholar
Nepf, H. M., Cowen, E. A., Kimmel, S. J. & Monismith, S. G. 1995 Longitudinal vortices under breaking waves. J. Geophys. Res. 100, 16111–16221.Google Scholar
Ruppert, D. & Wand, M. P. 1994 Multivariate locally weighted least squares regression. Ann. Statist. 22 (3), 1346–1370.CrossRefGoogle Scholar
Savitzky, A. & Golay, M. J. E. 1964 Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 36 (8), 1627–1639.Google Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455.Google Scholar
Sullivan, P. P. & McWilliams, J. C. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.CrossRefGoogle Scholar
Weber, J. E. & Saetra, Ø. 1995 Effect of film elasticity on the drift velocity of capillary-gravity waves. Phys. Fluids 7, 307–314.CrossRefGoogle Scholar