Hostname: page-component-5f745c7db-nzk4m Total loading time: 0 Render date: 2025-01-06T20:38:46.478Z Has data issue: true hasContentIssue false
  • English
  • Français

Experimental investigation of transitional flow in a toroidal pipe

Published online by Cambridge University Press:  13 December 2013

J. Kühnen ,
M. Holzner ,
B. Hof  and
H. C. Kuhlmann
J. Kühnen*
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Vienna University of Technology, Resselgasse 3/1/2, A-1040, Vienna, Austria IST Austria, Am Campus 1, 3400 Klosterneuburg, Austria
M. Holzner
Affiliation:
Institute of Environmental Engineering, ETH Zürich, Wolfgang Pauli Strasse 15, CH-8093 Zürich, Switzerland
B. Hof
Affiliation:
IST Austria, Am Campus 1, 3400 Klosterneuburg, Austria Max Planck Institute for Dynamics and Self Organization, Bunsenstrasse 10, D-37073 Göttingen, Germany
H. C. Kuhlmann
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Vienna University of Technology, Resselgasse 3/1/2, A-1040, Vienna, Austria
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow instability and further transition to turbulence in a toroidal pipe (torus) with curvature ratio (tube-to-coiling diameter) 0.049 is investigated experimentally. The flow inside the toroidal pipe is driven by a steel sphere fitted to the inner pipe diameter. The sphere is moved with constant azimuthal velocity from outside the torus by a moving magnet. The experiment is designed to investigate curved pipe flow by optical measurement techniques. Using stereoscopic particle image velocimetry, laser Doppler velocimetry and pressure drop measurements, the flow is measured for Reynolds numbers ranging from 1000 to 15 000. Time- and space-resolved velocity fields are obtained and analysed. The steady axisymmetric basic flow is strongly influenced by centrifugal effects. On an increase of the Reynolds number we find a sequence of bifurcations. 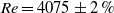For $\mathit{Re}= 4075\pm 2\hspace{0.167em} \% $ a supercritical bifurcation to an oscillatory flow is found in which waves travel in the streamwise direction with a phase velocity slightly faster than the mean flow. The oscillatory flow is superseded by a presumably quasi-periodic flow at a further increase of the Reynolds number before turbulence sets in. The results are found to be compatible, in general, with earlier experimental and numerical investigations on transition to turbulence in helical and curved pipes. However, important aspects of the bifurcation scenario differ considerably.

JFM classification

Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 463 - 491
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, M. 1934 Flow in curved tubes. Z. Angew. Math. Mech. 14, 257–275.Google Scholar
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.Google Scholar
Berger, S. A., Talbot, L. & Yao, L. S. 1983 Flow in curved pipes. Annu. Rev. Fluid Mech. 15, 461–512.CrossRefGoogle Scholar
Budwig, R. 1994 Refractive index matching methods for liquid flow investigations. Exp. Fluids 17, 350–355.Google Scholar
Cioncolini, A. & Santini, L. 2006 An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Therm. Fluid Sci. 30 (4), 367–380.CrossRefGoogle Scholar
Dean, W. R. 1927 Note on the motion of fluid in a curved pipe. Phil. Mag. 4, 208–223.Google Scholar
Dean, W. R. 1928 The streamline motion of fluid in a curved pipe. Phil. Mag. 7, 673–695.Google Scholar
van Doorne, C. W. H. & Westerweel, J. 2007 Measurement of laminar, transitional and turbulent pipe flow using stereoscopic-PIV. Exp. Fluids 42, 259–279.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Eckhardt, B. 2008 Turbulence transition in pipe flow: some open questions. Nonlinearity 21 (1), T1.CrossRefGoogle Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulent transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
Hasson, D. 1955 Streamline flow resistance in coils. Res. Corresp. 1, 1.Google Scholar
Hewitt, R. E., Hazel, A. L., Clarke, R. J. & Denier, J. P. 2011 Unsteady flow in a rotating torus after a sudden change in rotation rate. J. Fluid Mech. 688, 88–119.Google Scholar
Hof, B., van Doorne, C. W. H., Westerweel, J., Nieuwstadt, F. T. M. & Faisst, H. 2004 Experimental observation of nonlinear travelling waves in turbulent pipe flow. Science 305, 1594–1598.CrossRefGoogle ScholarPubMed
Hopkins, L. M., Kelly, J. T., Wexler, A. S. & Prasad, A. K. 2000 Particle image velocimetry measurements in complex geometries. Exp. Fluids 29, 91–95.Google Scholar
Hüttl, T. J. & Friedrich, R. 2000 Influence of curvature and torsion on turbulent flow in helically coiled pipes. Intl. J. Heat Fluid Flow 21, 345–353.Google Scholar
Hüttl, T. J. & Friedrich, R. 2001 Direct numerical simulation of turbulent flows in curved and helically coiled pipes. Comput. Fluids 30, 591–605.Google Scholar
Ito, H. 1959 Friction factors for turbulent flow in curved pipes. Trans. ASME J. Basic Engng. 81, 123–134.Google Scholar
Lowe, M. L. & Kutt, P. H. 1992 Refraction through cylindrical tubes. Exp. Fluids 13, 315–320.Google Scholar
Madden, F. N. & Mullin, T. 1994 The spin-up from rest of a fluid-filled torus. J. Fluid Mech. 265, 217–244.Google Scholar
Mishra, P. & Gupta, S. N. 1979 Momentum transfer in curved pipes. Part 1. Newtonian fluids. Part 2. Non-Newtonian fluids. Ind. Engng Chem. Process Des. Dev. 18, 130–137, 137–142.Google Scholar
Mullin, T. 2011 Experimental studies of transition to turbulence in a pipe. Annu. Rev. Fluid Mech. 43 (1), 1–24.Google Scholar
Naphon, P. & Wongwises, S. 2006 A review of flow and heat transfer characteristics in curved tubes. Renewable Sustainable Energy Rev. 10, 463–490.CrossRefGoogle Scholar
Piazza, I. D. & Ciofalo, M. 2011 Transition to turbulence in toroidal pipes. J. Fluid Mech. 687, 72–117.CrossRefGoogle Scholar
del Pino, C., Hewitt, R. E., Clarke, R. J., Mullin, T. & Denier, J. P. 2008 Unsteady fronts in the spin-down of a fluid-filled torus. Phys. Fluids 20 (12), 124104.CrossRefGoogle Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous and of the law of resistance in parallel channels. Phil. Trans. R. Soc. Lond. Ser. A 174, 935–982.Google Scholar
Sreenivasan, K. R. & Strykowski, P. J. 1983 Stabilization effects in flow through helically coiled pipes. Exp. Fluids 1, 31–36.Google Scholar
Taylor, G. I. 1929 The criterion for turbulence in curved pipes. Proc. R. Soc. Lond. A 124, 243–249.Google Scholar
Vashisth, S., Kumar, V. & Nigam, K. D. P. 2008 A review on the potential applications of curved geometries in process industry. Ind. Engng Chem. Res. 47 (10), 3291–3337.Google Scholar
Webster, D. R. & Humphrey, J. A. C. 1993 Experimental observation of flow instability in a helical coil. J. Fluids Engng 115 (3), 436–443.Google Scholar
Webster, D. R. & Humphrey, J. A. C. 1997 Traveling wave instability in helical coil flow. Phys. Fluids 9, 407–418.CrossRefGoogle Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar
White, C. M. 1929 Streamline flow through curved pipes. Proc. R. Soc. Lond. A 123, 645–663.Google Scholar

Kühnen et al. supplementary movie

Movie of a short section of the toroidal pipe from above at Re = 4350. The camera is following the flow with the velocity of the driving sphere, i.e. practically the bulk velocity of the flow.

Download Kühnen et al. supplementary movie(Video)
Video 15.5 MB
Supplementary material: Image

Kühnen et al. supplementary movie

Fully time-resolved oscillatory flow (shown are the contour lines of the streamwise velocity w in the cross-section of the toroidal pipe) during one period at Re=4300.

Download Kühnen et al. supplementary movie(Image)
Image 2 MB
Supplementary material: Image

Kühnen et al. supplementary movie

Vector fields of the cross-stream velocity fluctuations and selected contour lines of the streamwise velocity fluctuations during one period at Re=4300.

Download Kühnen et al. supplementary movie(Image)
Image 1.3 MB