Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T07:54:58.367Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of the turbulence induced by a bubble swarm rising within incident turbulence

Published online by Cambridge University Press:  27 July 2017

Elise Alméras ,
Varghese Mathai Open the ORCID record for Varghese Mathai [Opens in a new window] ,
Detlef Lohse Open the ORCID record for Detlef Lohse [Opens in a new window]  and
Chao Sun
Elise Alméras
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Varghese Mathai
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Detlef Lohse
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
Chao Sun*
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Center for Combustion Energy and Department of Thermal Engineering, Tsinghua University, Beijing 100084, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work reports an experimental characterisation of the flow properties in a homogeneous bubble swarm rising at high Reynolds numbers within a homogeneous and isotropic turbulent flow. Both the gas volume fraction $\unicode[STIX]{x1D6FC}$ and the velocity fluctuations 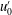$u_{0}^{\prime }$ of the carrier flow before bubble injection are varied, respectively, in the ranges 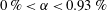$0\,\%<\unicode[STIX]{x1D6FC}<0.93\,\%$ and 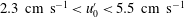$2.3~\text{cm}~\text{s}^{-1}<u_{0}^{\prime }<5.5~\text{cm}~\text{s}^{-1}$. The so-called bubblance parameter (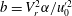$b=V_{r}^{2}\unicode[STIX]{x1D6FC}/u_{0}^{\prime 2}$, where 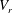$V_{r}$ is the bubble relative rise velocity) is used to compare the ratio of the kinetic energy generated by the bubbles to the one produced by the incident turbulence, and is varied from 0 to 1.3. Conditional measurements of the velocity field downstream of the bubbles in the vertical direction allow us to disentangle three regions that have specific statistical properties, namely the primary wake, the secondary wake and the far field. While the fluctuations in the primary wake are similar to that of a single bubble rising in a liquid at rest, the statistics of the velocity fluctuations in the far field follow a Gaussian distribution, similar to that produced by the homogenous and isotropic turbulence at the largest scales. In the secondary wake region, the conditional probability density function of the velocity fluctuations is asymmetric and shows an exponential tail for the positive fluctuations and a Gaussian one for the negative fluctuations. The overall agitation thus results from the combination of these three contributions and depends mainly on the bubblance parameter. For 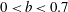$0<b<0.7$, the overall velocity fluctuations in the vertical direction evolve as 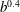$b^{0.4}$ and are mostly driven by the far-field agitation, whereas the fluctuations increase as 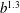$b^{1.3}$ for larger values of the bubblance parameter (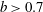$b>0.7$), in which the significant contributions come both from the secondary wake and the far field. Thus, the bubblance parameter is a suitable parameter to characterise the evolution of liquid agitation in bubbly turbulent flows.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase flow Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 825 , 25 August 2017 , pp. 1091 - 1112
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alméras, E., Cazin, S., Roig, V., Risso, F., Augier, F. & Plais, C. 2016 Time-resolved measurement of concentration fluctuations in a confined bubbly flow by lif. Intl J. Multiphase Flow 83, 153–161.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
van den Berg, T. H., Luther, S. & Lohse, D. 2006 Energy spectra in microbubbly turbulence. Phys. Fluids 18 (3), 8103.Google Scholar
Cisse, M., Saw, E.-W., Gibert, M., Bodenschatz, E. & Bec, J. 2015 Turbulence attenuation by large neutrally buoyant particles. Phys. Fluids 27 (6), 061702.Google Scholar
Colombet, D., Legendre, D., Risso, F., Cockx, A. & Guiraud, P. 2015 Dynamics and mass transfer of rising bubbles in a homogenous swarm at large gas volume fraction. J. Fluid Mech. 763, 254–285.Google Scholar
Darmana, D., Deen, N. G. & Kuipers, J. A. M. 2005 Detailed modeling of hydrodynamics, mass transfer and chemical reactions in a bubble column using a discrete bubble model. Chem. Engng Sci. 60 (12), 3383–3404.Google Scholar
Ellingsen, K., Risso, F., Roig, V. & Suzanne, C. 1997 Improvements of velocity measurements in bubbly flows by comparison of simultaneous hot-film and laser-doppler anemometry signals. In Proceedings of ASME Fluid Engng Div. Summer Meeting, Vancouver, Canada.Google Scholar
Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
Honkanen, M. 2009 Reconstruction of three-dimensional bubble surface from high-speed orthogonal imaging of dilute bubbly flow. In Proceedings of Comput. Meth. Multiphase flow V, pp. 469–480. WIT Press.Google Scholar
Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly air–water flow. J. Fluid Mech. 222, 95–118.CrossRefGoogle Scholar
Legendre, D., Merle, A. & Magnaudet, J. 2006 Wake of a spherical bubble or a solid sphere set fixed in a turbulent environment. Phys. Fluids 18 (4), 048102.Google Scholar
Mathai, V., Calzavarini, E., Brons, J., Sun, C. & Lohse, D. 2016a Microbubbles and microparticles are not faithful tracers of turbulent acceleration. Phys. Rev. Lett. 117 (2), 024501.CrossRefGoogle Scholar
Mathai, V., Neut, M. W. M., van der Poel, E. P. & Sun, C. 2016b Translational and rotational dynamics of a large buoyant sphere in turbulence. Exp. Fluids 57 (4), 1–10.CrossRefGoogle Scholar
Mathai, V., Prakash, V. N., Brons, J., Sun, C. & Lohse, D. 2015 Wake-driven dynamics of finite-sized buoyant spheres in turbulence. Phys. Rev. Lett. 115 (12), 124501.Google Scholar
Mazzitelli, I. M. & Lohse, D. 2004 Lagrangian statistics for fluid particles and bubbles in turbulence. New J. Phys. 6 (1), 203.Google Scholar
Mazzitelli, I. M., Lohse, D. & Toschi, F. 2003 The effect of microbubbles on developed turbulence. Phys. Fluids 15 (1), L5–L8.CrossRefGoogle Scholar
Mendez-Diaz, S., Serrano-Garcia, J. C., Zenit, R. & Hernandez-Cordero, J. A. 2013 Power spectral distributions of pseudo-turbulent bubbly flows. Phys. Fluids 25 (4), 043303.Google Scholar
Mercado, J. M., Gomez, D. C., Van Gils, D., Sun, C. & Lohse, D. 2010 On bubble clustering and energy spectra in pseudo-turbulence. J. Fluid Mech. 650, 287–306.Google Scholar
Mercado, J. M., Prakash, V. N., Tagawa, Y., Sun, C. & Lohse, D. 2012 Lagrangian statistics of light particles in turbulence. Phys. Fluids 24 (5), 055106.Google Scholar
Poorte, R. E. G. & Biesheuvel, A. 2002 Experiments on the motion of gas bubbles in turbulence generated by an active grid. J. Fluid Mech. 461, 127–154.Google Scholar
Pope, S. B. 2000 Turbulent Flow. Cambridge University Press.Google Scholar
Prakash, V. N., Mercado, J. M., van Wijngaarden, L., Mancilla, E., Tagawa, Y., Lohse, D. & Sun, C. 2016 Energy spectra in turbulent bubbly flows. J. Fluid Mech. 791, 174–190.Google Scholar
Rensen, J., Luther, S. & Lohse, D. 2005 The effect of bubbles on developed turbulence. J. Fluid Mech. 538, 153–187.Google Scholar
Riboux, G., Legendre, D. & Risso, F. 2013 A model of bubble-induced turbulence based on large-scale wake interactions. J. Fluid Mech. 719, 362–387.Google Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.Google Scholar
Risso, F. 2016 Physical interpretation of probability density functions of bubble-induced agitation. J. Fluid Mech. 809, 240.Google Scholar
Risso, F. & Ellingsen, K. 2002 Velocity fluctuations in a homogeneous dilute dispersion of high-Reynolds-number rising bubbles. J. Fluid Mech. 453, 395–410.CrossRefGoogle Scholar
Roghair, I., Mercado, J. M., Annaland, M. V. S., Kuipers, H., Sun, C. & Lohse, D. 2011 Energy spectra and bubble velocity distributions in pseudo-turbulence: numerical simulations versus experiments. Intl J. Multiphase Flow 37 (9), 1093–1098.Google Scholar
Roig, V. & De Tournemine, A. L. 2007 Measurement of interstitial velocity of homogeneous bubbly flows at low to moderate void fraction. J. Fluid Mech. 572, 87–110.Google Scholar
Shew, W. L., Poncet, S. & Pinton, J. 2006 Force measurements on rising bubbles. J. Fluid Mech. 569 (1), 51–60.CrossRefGoogle Scholar
Van der Hoef, M. A., van Sint Annaland, M., Deen, N. G. & Kuipers, J. A. M. 2008 Numerical simulation of dense gas–solid fluidized beds: a multiscale modeling strategy. Annu. Rev. Fluid Mech. 40, 47–70.Google Scholar
Van Wijngaarden, L. 1998 On pseudo turbulence. Theor. Comput. Fluid Dyn. 10 (1), 449–458.CrossRefGoogle Scholar
Wu, M. & Gharib, M. 2002 Experimental studies on the shape and path of small air bubbles rising in clean water. Phys. Fluids 14 (7), L49–L52.Google Scholar