Published online by Cambridge University Press: 10 January 2024
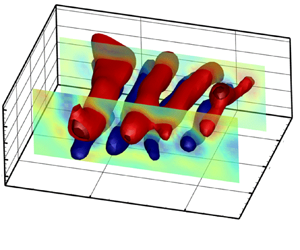
Flow-induced vibration (FIV) of a flexible cylinder with a triangular cross-section, allowed to oscillate in the cross-flow, inline and torsional direction, is studied experimentally through water tunnel tests. The dynamic response of the cylinder was studied for three different angles of attack ( $0^\circ, 30^\circ, 60^\circ$), at reduced velocities of 0.9–16.27, corresponding to Reynolds numbers of 364–3600. At the angle of attack of
$0^\circ, 30^\circ, 60^\circ$), at reduced velocities of 0.9–16.27, corresponding to Reynolds numbers of 364–3600. At the angle of attack of  $0^\circ$, vortex-induced vibration at low reduced velocity was observed, which transitioned to galloping at higher reduced velocities. At the angles of attack of
$0^\circ$, vortex-induced vibration at low reduced velocity was observed, which transitioned to galloping at higher reduced velocities. At the angles of attack of  $30^\circ$ and
$30^\circ$ and  $60^\circ$, galloping-type response was observed over the range of the reduced velocities tested. Our results show that the cylinder's torsional oscillation breaks the system's symmetry and affects the structural response at higher reduced velocities regardless of the angle of attack. The FIV response of the flexible triangular cylinder is distinct from that of a rigid flexibly mounted triangular cylinder due to torsional oscillation, spanwise flexibility and the two fixed boundary conditions limiting the amplitude of oscillation. Flow field analysis in the wake of the cylinder was done qualitatively and quantitatively using hydrogen bubble flow visualisation and time-resolved volumetric particle tracking velocimetry techniques, respectively. Our results show the existence of highly three-dimensional vortex structures in the wake of the cylinder. We studied the coupling between the vortex shedding modes in the wake of the cylinder and the structural vibration modes through the spatiotemporal mode analysis using the proper orthogonal decomposition technique to distinguish between different types of the FIV response observed.
$60^\circ$, galloping-type response was observed over the range of the reduced velocities tested. Our results show that the cylinder's torsional oscillation breaks the system's symmetry and affects the structural response at higher reduced velocities regardless of the angle of attack. The FIV response of the flexible triangular cylinder is distinct from that of a rigid flexibly mounted triangular cylinder due to torsional oscillation, spanwise flexibility and the two fixed boundary conditions limiting the amplitude of oscillation. Flow field analysis in the wake of the cylinder was done qualitatively and quantitatively using hydrogen bubble flow visualisation and time-resolved volumetric particle tracking velocimetry techniques, respectively. Our results show the existence of highly three-dimensional vortex structures in the wake of the cylinder. We studied the coupling between the vortex shedding modes in the wake of the cylinder and the structural vibration modes through the spatiotemporal mode analysis using the proper orthogonal decomposition technique to distinguish between different types of the FIV response observed.