Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T04:31:10.097Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of dissipation-element statistics in scalar fields of a jet flow

Published online by Cambridge University Press:  29 April 2013

Markus Gampert ,
Philip Schaefer  and
Norbert Peters
Markus Gampert*
Affiliation:
Institute for Combustion Technology, RWTH-Aachen University, Templergraben 64, Aachen, Germany
Philip Schaefer
Affiliation:
Institute for Combustion Technology, RWTH-Aachen University, Templergraben 64, Aachen, Germany
Norbert Peters
Affiliation:
Institute for Combustion Technology, RWTH-Aachen University, Templergraben 64, Aachen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a detailed experimental investigation of conditional statistics obtained from dissipation elements based on the passive scalar field 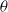$\theta $ and its instantaneous scalar dissipation rate 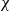$\chi $. Using high-frequency planar Rayleigh scattering measurements of propane discharging as a round turbulent jet into coflowing carbon dioxide, we acquire with Taylor’s hypothesis a highly resolved three-dimensional field of the propane mass fraction 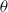$\theta $. The Reynolds number (based on nozzle diameter and jet exit velocity) varies between 3000 and 8600. The experimental results for the joint probability density of the scalar difference 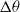$ \mathrm{\Delta} \theta $ and the length 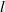$l$ of dissipation elements resembles those previously obtained from direct numerical simulations of Wang & Peters (J. Fluid Mech., vol. 554, 2006, pp. 457–475). In addition, the normalized marginal probability density function 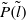$\tilde {P} (\tilde {l} )$ of the length of dissipation elements follows closely the theoretical model derived by Wang & Peters (J. Fluid Mech., vol. 608, 2008, pp. 113–138). We also find that the mean linear distance 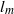${l}_{m} $ between two extreme points of an element is of the order of the scalar Taylor microscale 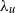${\lambda }_{u} $. Furthermore, the conditional mean 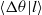$\langle \mathrm{\Delta} \theta \vert l\rangle $ scales with Kolmogorov’s 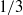$1/ 3$ power law. The investigation of the orientation of long dissipation elements in the jet flow reveals a preferential alignment, perpendicular to the streamwise direction for long elements, while the orientation of short elements is close to isotropic. Following an approach proposed by Kholmyansky & Tsinober (Phys. Lett. A, vol. 373, 2009, pp. 2364–2367), we finally investigate the probability density function of the scalar increment 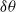$\delta \theta $ in the streamwise direction, when strong dissipative events are either retained in or excluded from the measurement volume. In the present study, however, these events are related to maximum points of the scalar dissipation rate 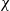$\chi $ together with their local extent. When these regions are excluded from the scalar field, we observe a tendency of the probability density function 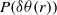$P(\delta \theta (r))$ towards a Gaussian bell-shaped curve.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Turbulence theory Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 337 - 366
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldudak, F. & Oberlack, M. 2012 Dissipation element analysis in turbulent channel flow. J. Fluid Mech. 694, 332–351.CrossRefGoogle Scholar
Anselmet, F. & Antonia, R. A. 1985 Joint statistics between temperature and its dissipation in a turbulent jet. Phys. Fluids 28, 1048–1054.CrossRefGoogle Scholar
Antonia, R. A., Hopfinger, E., Gagne, Y. & Anselmet, F. 1984 Temperature structure functions in turbulent shear flows. Phys. Rev. A 30, 2704–2707.CrossRefGoogle Scholar
Antonia, R. A. & Sreenivasan, K. R. 1977 Log-normality of temperature dissipation in a turbulent boundary layer. Phys. Fluids 20, 1800–1804.CrossRefGoogle Scholar
Antonia, R. A. & Van Atta, C. W. 1975 On the correlation between temperature and velocity dissipation fields in a heated turbulent jet. J. Fluid Mech. 67, 273–288.CrossRefGoogle Scholar
Bermejo-Moreno, I. & Pullin, D. I. 2008 On the non-local geometry of turbulence. J. Fluid Mech. 603, 101–135.CrossRefGoogle Scholar
Bremer, P., Bringa, E., Duchaineau, M., Gyulassy, A., Laney, D., Mascarenhas, A. & Pascucci, V. 2007 Topological feature extraction and tracking. J. Phys.: Conf. Ser. 78, 012007.Google Scholar
Cai, J., Dinger, M., Li, W., Carter, C., Ryan, M. & Tong, C. 2011 Experimental study of three-scalar mixing in a turbulent coaxial jet. J. Fluid Mech. 685, 495–531.CrossRefGoogle Scholar
Celani, A., Lanotte, A., Mazzino, A. & Vergassola, M. 2000 Universality and saturation of intermittency in passive scalar turbulence. Phys. Rev. Lett. 84 (11), 2385–2388.CrossRefGoogle ScholarPubMed
Celani, A., Lanotte, A., Mazzino, A. & Vergassola, M. 2001 Fronts in passive scalar turbulence. Phys. Fluids 13 (6), 1768–1783.CrossRefGoogle Scholar
Chertkov, M. & Falkovich, G. 1996 Anomalous scaling exponents of a white-advected passive scalar. Phys. Rev. Lett. 76, 2706–2709.CrossRefGoogle ScholarPubMed
Chertkov, M., Falkovich, G., Kolokolov, I. & Lebedev, V. 1995 Statistics of a passive scalar advected by a large-scale two-dimensional velocity field: analytic solution. Phys. Rev. E 51, 5609–5627.CrossRefGoogle ScholarPubMed
Corrsin, S. 1951 On the spectrum of isotropic temperature field in isotropic turbulence. J. Appl. Phys. 22, 469–473.CrossRefGoogle Scholar
Dahm, W. J. A. & Southerland, K. B. 1997 Experimental assessment of Taylor’s hypothesis and its applicability to dissipation estimates in turbulent flows. Phys. Fluids 9, 2101–2107.CrossRefGoogle Scholar
Dávila, J. & Vassilicos, J. C. 2003 Richardson’s pair diffusion and the stagnation point structure of turbulence. Phys. Rev. Lett. 91, 144–501.CrossRefGoogle ScholarPubMed
Dibble, R., Warnatz, J. & Maas, U. 1996 Combustion: Physical and Chemical Fundamentals, Modelling and Simulations, Experiments, Pollutant Formation. Springer.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.CrossRefGoogle Scholar
Dowling, D. R. & Dimotakis, P. E. 1990 Similarity of the concentration field of gas-phase turbulent jets. J. Fluid Mech. 218, 109–141.CrossRefGoogle Scholar
Eckbreth, A. 1996 Laser Diagnostics for Combustion Temperature and Species, 2nd edn. Informa Healthcare.Google Scholar
Friehe, C. A., Van Atta, C. W. & Gibson, C. H. 1971 Jet turbulence dissipation rate measurements and correlations. AGARD Conf. Turbul. Shear Flows CP-93, 18.1–18.7.Google Scholar
Gampert, M., Goebbert, J. H., Schaefer, P., Gauding, M., Peters, N., Aldudak, F. & Oberlack, M. 2011 Extensive strain along gradient trajectories in the turbulent kinetic energy field. New J. Phys. 13, 043012.CrossRefGoogle Scholar
Gampert, M., Narayanaswamy, V. & Peters, N. 2012a Scalar gradient trajectory measurements using high-frequency cinematographic planar Rayleigh scattering. Exp. Fluids (submitted).Google Scholar
Gampert, M., Narayanaswamy, V., Schaefer, P. & Peters, N. 2012b Conditional statistics of the turbulent/non-turbulent interface in a jet flow. J. Fluid Mech. (submitted).Google Scholar
Gampert, M., Schaefer, P., Goebbert, J. & Peters, N. 2012c Decomposition of the field of the turbulent kinetic energy into regions of compressive and extensive strain. Phys. Scr. T (in press).Google Scholar
Gampert, M., Schaefer, P., Narayanaswamy, V. & Peters, N. 2013 Gradient trajectory analysis in a jet flow for turbulent combustion modelling. J. Turbul. 14, 147–164.CrossRefGoogle Scholar
Gibson, C. H. 1968 Fine structure of scalar fields mixed by turbulence i. Zero gradient points and minimal gradient surfaces. Phys. Fluids 11, 2305–2315.CrossRefGoogle Scholar
Goto, S. & Vassilicos, J. C. 2009 The dissipation rate coefficient is not universal and depends on the internal stagnation point structure. Phys. Fluids 21, 035104.CrossRefGoogle Scholar
Hearst, R., Buxton, O., Ganapathisubramani, B. & Lavoie, P. 2012 Experimental estimation of fluctuating velocity and scalar gradients in turbulence. Exp. Fluids 53, 925–942.CrossRefGoogle Scholar
Holzer, M. & Siggia, E. D. 1994 Turbulent mixing of a passive scalar. Phys. Fluids 6, 1820–1837.CrossRefGoogle Scholar
Jimenez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.CrossRefGoogle Scholar
Kholmyansky, M. & Tsinober, A. 2009 On an alternative explanation of anomalous scaling and how well-defined is the concept of inertial range. Phys. Lett. A 373, 2364–2367.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941a The local structure of turbulence in an incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kolmogorov, A. N. 1941b Dissipation of energy under locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 16–18.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.CrossRefGoogle Scholar
Korchashkin, N. N. 1970 The effect of fluctuations of energy dissipation and temperature dissipation on locally isotropic turbulent fields. Izv. Atmos. Oceanic Phys. 6, 947–949.Google Scholar
Kraichnan, R. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11, 945–953.CrossRefGoogle Scholar
Kraichnan, R. 1974 Convection of a passive scalar by a quasi-uniform random straining field. J. Fluid Mech. 64, 737–762.CrossRefGoogle Scholar
Kraichnan, R. 1994 Anomalous scaling of a randomly advected passive scalar. Phys. Rev. Lett. 72, 1016–1019.CrossRefGoogle ScholarPubMed
Laney, D., Bremer, P., Mascarenhas, A., Miller, P. & Pascucci, V. 2007 Understanding the structure of the turbulent mixing layer in hydrodynamic instabilities. IEEE Trans. Vis. Comput. Graphics 12, 1053–1060.CrossRefGoogle Scholar
Lundgren, T. S. 2002 Kolmogorov two thirds law by matched asymptotic expansion. Phys. Fluids 14, 638–642.CrossRefGoogle Scholar
Mellado, J. P., Wang, L. & Peters, N. 2009 Gradient trajectory analysis of a scalar field with internal intermittency. J. Fluid Mech. 626, 333–365.CrossRefGoogle Scholar
Meneveau, C., Sreenivasan, K. R., Kailasnath, P. & Fan, M. S. 1990 Joint multifractal measures: Theory and applications to turbulence. Phys. Rev. A 41, 894–913.CrossRefGoogle Scholar
Miyauchi, T. & Tanahashi, M. 2001 Coherent fine scale structure in turbulence. In IUTAM Symposium on Geometry and Statistics of Turbulence (ed. Kambe, T., Nakano, T. & Miyauchi, T.), pp. 67–75. Kluwer.CrossRefGoogle Scholar
Mydlarski, L. & Warhaft, Z. 1998 Passive scalar statistics in high-Péclet-number grid turbulence. J. Fluid Mech. 358, 135–175.CrossRefGoogle Scholar
Obukhov, A. R. 1949 The structure of the temperature field in a turbulent flow. Izv. Akad. Nauk. SSSR, Geogr. Geophys. 13, 58–69.Google Scholar
Obukhov, A. R. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13, 77–81.CrossRefGoogle Scholar
Pascucci, V., Tricoche, X., Hagen, H. & Tierny, J. 2011 Topological Methods In Data Analysis and Visualization, 1st edn. Springer.CrossRefGoogle Scholar
Peters, N. 2000 Turbulent Combustion. Cambridge University Press.CrossRefGoogle Scholar
Peters, N. 2009 Multiscale combustion and turbulence. In 32nd Symposium on Combustion, Montreal 2008, Proc. Combust. Inst., vol. 32, pp. 1–25.Google Scholar
Peters, N., Kerschgens, B. & Paczko, G. 2013 Super-Knock Prediction Using a Refined Theory of Turbulence, SAE 2013-01-1109.CrossRefGoogle Scholar
Schaefer, L., Dierksheide, U., Klaas, M. & Schroeder, W. 2010a Investigation of dissipation elements in a fully developed turbulent channel flow by tomographic particle-image velocimetry. Phys. Fluids 23, 035106.CrossRefGoogle Scholar
Schaefer, P., Gampert, M., Goebbert, J. H., Wang, L. & Peters, N. 2010b Testing of different model equations for the mean dissipation using Kolmogorov flows. Flow Turbul. Combust 85, 225–243.CrossRefGoogle Scholar
Schaefer, P., Gampert, M., Gauding, M., Peters, N. & Treviño, C. 2011 The secondary splitting of zero-gradient points in a scalar field. J. Engng Maths 71 (1), 81–95.CrossRefGoogle Scholar
Schaefer, P., Gampert, M. & Peters, N. 2012a The length distribution of streamline segments in homogeneous isotropic decaying turbulence. Phys. Fluids 24, 045104.CrossRefGoogle Scholar
Schaefer, L., Goebbert, J. & Schroeder, W. 2012b Dissipation element analysis in experimental and numerical shear flow. Eur. J. Mech. (B/Fluids) 38, 85–92.CrossRefGoogle Scholar
Schaefer, P., Gampert, M. & Peters, N. 2013a Joint statistics and conditional mean strain rates of streamline segments. Phys. Scr. T (in press).CrossRefGoogle Scholar
Schaefer, P., Gampert, M. & Peters, N. 2013b On the scaling of the mean length of streamline segments in various turbulent flows. C. R. Mec. 340, 859–866.CrossRefGoogle Scholar
Schaefer, P., Gampert, M., Wang, L. & Peters, N. 2009 Fast and slow changes of the length of gradient trajectories in homogenous shear turbulence. In Advances in Turbulence XII (ed. Eckhardt, B.). pp. 565–572. Springer.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K. R. & Yakhot, V. 2007 Asymptotic exponents from low-Reynolds-number flows. New J. Phys. 9, 89.CrossRefGoogle Scholar
Shraiman, B. I. & Siggia, E. D. 2000 Scalar turbulence. Nature 405, 639–646.CrossRefGoogle ScholarPubMed
Smale, S. 1961a Generalized Poincare’s conjecture in dimensions greater than four. Ann. Maths 74, 391–406.CrossRefGoogle Scholar
Smale, S. 1961b On gradient dynamical systems. Ann. Maths 74, 199–206.CrossRefGoogle Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent shear flows. Proc. R. Soc. Lond. A 434, 165–182.Google Scholar
Sreenivasan, K. R. 1996 The passive scalar spectrum and the Obukhov–Corrsin constant. Phys. Fluids 8, 189–196.CrossRefGoogle Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Sreenivasan, K. R., Antonia, R. A. & Danh, H. Q. 1977 Temperature dissipation fluctuations in a turbulent boundary layer. Phys. Fluids 20, 1238–1249.CrossRefGoogle Scholar
Stolovitzky, G., Kailasnath, P. & Sreenivasan, K. R. 1995 Refined similarity hypotheses for passive scalars mixed by turbulence. J. Fluid Mech. 297, 275–291.CrossRefGoogle Scholar
Su, L. K. & Clemens, N. T. 1999 Planar measurements of the full three-dimensional scalar dissipation rate in gas-phase turbulent flows. Exp. Fluids 27, 507–521.CrossRefGoogle Scholar
Su, L. K. & Clemens, N. T. 2003 The structure of fine-scale scalar mixing in gas-phase planar turbulent jets. J. Fluid Mech. 488, 1–29.CrossRefGoogle Scholar
Talbot, B., Mazellier, N., Renou, B., Danaila, L. & Boukhalfa, M. 2009 Time-resolved velocity and concentration measurements in variable-viscosity turbulent jet flow. Exp. Fluids 47, 769–787.CrossRefGoogle Scholar
Tropea, C., Yarin, A. & Foss, J. 2007 Springer Handbook of Experimental Fluid Mechanics. Springer.CrossRefGoogle Scholar
Tsinober, A. 2001 An Informal Introduction to Turbulence. Kluwer.CrossRefGoogle Scholar
Tsinober, A., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity gradients in turbulent flows. J. Fluid Mech. 242, 169–192.CrossRefGoogle Scholar
Van Atta, C. W. 1971 Influence of fluctuations in local dissipation rates on turbulent scalar characteristics in the inertial subrange. Phys. Fluids 14, 1803–1804.CrossRefGoogle Scholar
Wang, L. 2009 Scaling of the two-point velocity difference along scalar gradient trajectories in fluid turbulence. Phys. Rev. E 79, 046325.CrossRefGoogle ScholarPubMed
Wang, L. 2010 On properties of fluid turbulence along streamlines. J. Fluid Mech. 648, 183–203.CrossRefGoogle Scholar
Wang, L. & Peters, N. 2006 The length scale distribution function of the distance between extremal points in passive scalar turbulence. J. Fluid Mech. 554, 457–475.CrossRefGoogle Scholar
Wang, L. & Peters, N. 2008 Length scale distribution functions and conditional means for various fields in turbulence. J. Fluid Mech. 608, 113–138.CrossRefGoogle Scholar
Wang, L. & Peters, N. 2013 A new view of flow topology and conditional statistics in turbulence. Phil. Trans. R. Soc. Lond. A 371, 1982.Google ScholarPubMed
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 302–240.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2004 Statistics of a passive scalar in homogeneous turbulence. New J. Phys. 6 (40), 010040.CrossRefGoogle Scholar
Wray, A. & Hunt, J. 1990 Algorithms for classification of turbulent structures. In Topological Fluid Mechanics (ed. Moffatt, H. K. & Tsinober, A.), pp. 95–104. Cambridge University Press.Google Scholar
Zhou, Y. & Antonia, R. A. 1993 Temperature dissipation measurements in a fully developed turbulent channel flow. Exp. Fluids 15, 191–199.CrossRefGoogle Scholar
Zhou, Y., Antonia, R. A. & Hosokawa, I. 1995 Refined similarity hypotheses for turbulent velocity and temperature fields. Phys. Fluids 7, 1637–1648.CrossRefGoogle Scholar