No CrossRef data available.
Article contents
Exotic flotation theory with new method for floating stability analysis
Published online by Cambridge University Press: 18 October 2023
Abstract
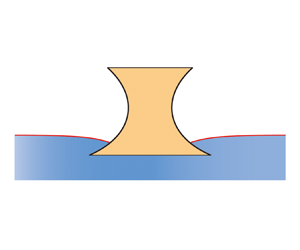
A macroscale floating object moving downwards will encounter an increasing buoyancy force exerted by the liquid. However, considering the surface tension and the deformed meniscus, we find an exotic floating object of specific shape that withstands a constant total force exerted by the liquid when it moves vertically and slowly. This constant total force consists of the surface tension force and the hydrostatic pressure force, from which a model to determine the shape of the exotic floating object is proposed. Results show that there exist three types of exotic floating objects in both the two-dimensional symmetric and axisymmetric cases, dependent on their concavity and convexity. To ensure that the menisci around the exotic floating objects can be sustained in practice, the stabilities of these menisci are checked. Apart from the meniscus stabilities (of liquid surfaces), the floating stabilities (of solid objects) are also studied. It is demonstrated that the exotic floating object remains in a critical state of floating stabilities no matter where this object locates vertically, from which a new method to predict the floating stabilities for general floating objects of arbitrary shape is put forward, based on the contact angle and the geometrical parameters at the contact point. With the new method, the floating stabilities can be predicted conveniently, without performing an extra force analysis.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press



