Article contents
Exact solutions for steadily travelling water waves with submerged point vortices
Published online by Cambridge University Press: 09 January 2023
Abstract
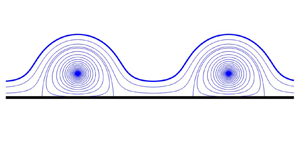
This paper presents a novel theoretical framework, based on the concept of the Schwarz function of a wave, for understanding water waves with vorticity in the absence of gravity and capillarity. The framework leads naturally to a taxonomy of three subcases, herein referred to as cases 1, 2 and 3, into which fall three existing studies of water waves incorporating uniform vorticity and submerged point vortices. This provides a theoretical unification of several seemingly unrelated results in the literature. It also provides a route to finding new exact solutions with this paper focussing on new solutions falling within the case 2 category. Among several presented here are a submerged point vortex pair cotravelling with a solitary deep-water wave, von Kármán point vortex streets cotravelling with a periodic deep-water wave and a point vortex row cotravelling with a wave in water of finite depth. Some other more exotic waveforms are also constructed. All these new solutions generalize those of Crowdy & Roenby (Fluid Dyn. Res., vol. 46, 2014) who found steady waves in deep water cotravelling with a submerged point vortex row for which the free surface shapes turn out to coincide with those of pure capillary waves on deep water found by Crapper (J. Fluid Mech., vol. 2, 1957). The new exact solutions are likely to provide a useful basis for asymptotic or numerical studies when additional effects such as gravity and capillarity are incorporated.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by



