Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T14:45:15.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact coherent structures in stably stratified plane Couette flow

Published online by Cambridge University Press:  08 August 2017

D. Olvera Open the ORCID record for D. Olvera [Opens in a new window]  and
R. R. Kerswell
D. Olvera*
Affiliation:
School of Mathematics, University of Bristol, BristolBS8 1TW, UK
R. R. Kerswell
Affiliation:
School of Mathematics, University of Bristol, BristolBS8 1TW, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The existence of exact coherent structures in stably stratified plane Couette flow (gravity perpendicular to the plates) is investigated over Reynolds–Richardson number (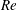$Re$–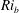$Ri_{b}$) space for a fluid of unit Prandtl number 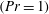$(Pr=1)$ using a combination of numerical and asymptotic techniques. Two states are repeatedly discovered using edge tracking – EQ7 and EQ7-1 in the nomenclature of Gibson & Brand (J. Fluid Mech., vol. 745, 2014, pp. 25–61) – and found to connect with two-dimensional convective roll solutions when tracked to negative 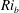$Ri_{b}$ (the Rayleigh–Bénard problem with shear). Both these states and Nagata’s (J. Fluid Mech., vol. 217, 1990, pp. 519–527) original exact solution feel the presence of stable stratification when 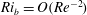$Ri_{b}=O(Re^{-2})$ or equivalently when the Rayleigh number 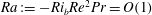$Ra:=-Ri_{b}Re^{2}Pr=O(1)$. This is confirmed via a stratified extension of the vortex wave interaction theory of Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). If the stratification is increased further, EQ7 is found to progressively spanwise and cross-stream localise until a second regime is entered at 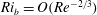$Ri_{b}=O(Re^{-2/3})$. This corresponds to a stratified version of the boundary region equations regime of Deguchi, Hall & Walton (J. Fluid Mech., vol. 721, 2013, pp. 58–85). Increasing the stratification further appears to lead to a third, ultimate regime where 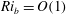$Ri_{b}=O(1)$ in which the flow fully localises in all three directions at the minimal Kolmogorov scale which then corresponds to the Osmidov scale. Implications for the laminar–turbulent boundary in th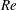e ($Re$–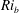$Ri_{b}$) plane are briefly discussed.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Turbulent Flows: Stratified turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 583 - 614
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 449, 1–42.Google Scholar
Blackburn, H. M., Hall, P. & Sherwin, S. J. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 726, R2.Google Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595.Google Scholar
Clever, R. M. & Busse, F. H. 1992 Three-dimensional convection in a horizontal fluid layer subjected to a constant shear. J. Fluid Mech. 234, 511–527.Google Scholar
Clever, R. M. & Busse, F. H. 2000 Tertiary and quarternary solutions for plane Couette flow with thermal stratification. In 11th International Couette-Taylor Workshop Held at Bremen, Germany, 1999: Physics of Rotating Fluids (ed. Egbers, C. & Pfister, G.), Lecture Notes In Physics, vol. 549, pp. 399–416. Springer.Google Scholar
Clever, R. M., Busse, F. H. & Kelly, R. E. 1977 Instabilities of longitudinal convection rolls in Couette flow. Z. Angew. Math. Phys. 28, 771–783.Google Scholar
Davey, A. & Reid, W. H. 1977 On the stability of stratified viscous plane Couette flow. Part 2. Variable buoyancy frequency. J. Fluid Mech. 80, 509–525.Google Scholar
Deguchi, K. 2015 Self-sustained states at Kolmogorov microscale. J. Fluid Mech. 781, R6.Google Scholar
Deguchi, K. 2017 Scaling of small vortices in stably stratified shear flows. J. Fluid Mech. 821, 582–594.Google Scholar
Deguchi, K. & Hall, P. 2014 Canonical exact coherent structures embedded in high Reynolds number flows. Phil. Trans. R. Soc. Lond. 372, 20130352.Google Scholar
Deguchi, K. & Hall, P. 2015 Asymptotic descriptions of oblique coherent structures in shear flows. J. Fluid Mech. 782, 356–367.Google Scholar
Deguchi, K., Hall, P. & Walton, A. G. 2013 The emergence of localized vortex-wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.Google Scholar
Deusebio, E., Caulfield, C. P. & Taylor, J. R. 2015 The intermittency boundary in stratified plane Couette flow. J. Fluid Mech. 781, 298–329.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Duguet, Y., Brandt, L. & Larsson, B. R. 2010 Towards minimal perturbations in transitional plane Couette flow. Phys. Rev. E 82, 026316.Google Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2008 Transition in pipe flow: the saddle structure on the boundary of turbulence. J. Fluid Mech. 613, 255–274.Google Scholar
Eaves, T. S. & Caulfield, C. P. 2015 Disruption of SSP/VWI states by stable stratification. J. Fluid Mech. 784, 548–564.Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Garcia-Villalba, M. & del Alamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23, 045104.Google Scholar
Gibson, J. F. & Brand, E. 2014 Spanwise-localized solutions of planar shear flows. J. Fluid Mech. 745, 25–61.Google Scholar
Gibson, J. F. & Cvitanović, P. 2010 Geometry of the turbulence in wall-bounded shear flows: periodic orbits. Phys. Scr. 142, 014007.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Generalis, S. & Nagata, M. 2003 Transition in homogeneously heated inclined plane parallel shear flows. Trans. ASME J. Heat Transfer. 125, 795–803.Google Scholar
Hall, P. 2012 Vortex-wave interactions/self-sustained processes in high Prandtl number natural convection in a vertical channel with moving sidewalls. Stud. Appl. Maths 129, 1–25.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent strctures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Hof, B., van Doorne, C. W. H., Westerweel, J., Nieuwstadt, F. T. M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear travelling waves in turbulent pipe flow. Science 305, 1594–1598.Google Scholar
Howard, L. N. & Maslowe, S. A. 1973 Stability of stratified shear flows. Boundary-Layer Meteorol. 4, 511–523.Google Scholar
Huppert 1973 Howard’s technique for perturbing neutral solutions of the Taylor-Goldstein equation. J. Fluid Mech. 57, 361–368.Google Scholar
Itano, T. & Generalis, S. C. 2009 Hairpin vortex solution in planar Couette flow: a tapestry of knotted vortices. Phys. Rev. Lett. 102, 114501.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.Google Scholar
Joseph, D. D. 1966 Nonlinear stability of the Boussinesq equations by the method of energy. Arch. Rat. Mech. Anal. 22, 163–184.CrossRefGoogle Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.Google Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44, 203–225.Google Scholar
Kelly, R. E. 1977 The onset and development of Rayleigh–Benard convection in shear flows: a review. In Physicochemical Hydrodynamics (ed. Spaulding, D. B.), pp. 65–79. Advance Publications.Google Scholar
Kerswell, R. R. 2005 Recent progress in understanding the transition to turbulence in a pipe. Nonlinearity 18, R17–R44.Google Scholar
Kerswell, R. R. & Tutty, O. R. 2007 Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
Lucas, D. & Kerswell, R. R. 2015 Recurrent flow analysis in spatiotemporally chaotic 2-dimensional Kolmogorov flow. Phys. Fluids 27, 045106.Google Scholar
Mellibovsky, F., Meseguer, A., Schneider, T. M. & Eckhardt, B. 2009 Transition in localized pipe flow turbulene. Phys. Rev. Lett. 103, 054502.Google Scholar
Nagata, M. 1990 3-Dimensional finite-amplitude solutions in plane Couette flow – bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Olvera, D. & Kerswell, R. R.2017 Optimising energy growth as a tool for finding exact coherent structures. Phys. Rev. Fluids (submitted) arXiv:1701.09103.Google Scholar
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of turbulence. J. Fluid Mech. 702, 415–443.Google Scholar
Rabin, S. M. E., Caulfield, C. P. & Kerswell, R. R. 2012 Triggering turbulence efficiently in plane Couette flow. J. Fluid Mech. 712, 244–272.Google Scholar
Schneider, T. M. & Eckhardt, B. 2009 Edge states intermediate between laminar and turbulent dynamics in pipe flow. Phil. Trans. R. Soc. Lond. 1888, 577–587.Google Scholar
Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett. 99, 034502.Google Scholar
Schneider, T. M., Gibson, J. F., Lagher, M., De Lillo, F. & Eckhardt, B. 2008 Laminar-turbulent boundary in plane Couette flow. Phys. Rev. E 78, 037301.Google Scholar
Schneider, T. M., Gibson, T. M. & Burke, J. 2010a Snakes and ladders: localized solutions in plane Couette flow. Phys. Rev. Lett. 104, 104501.Google Scholar
Schneider, T. M., Marinc, D. & Eckhardt, B. 2010b Localized edge states nucleate turbulence in extended plane Couette cells. J. Fluid Mech. 646, 441–451.CrossRefGoogle Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.Google Scholar
Taylor, J. R.2008 Numerical simulations of the stratified oceanic bottom boundary layer, PhD thesis, Mechanical Engineering, University of California, San Diego (see http://www.damtp.cam.ac.uk/user/jrt51/files.html for Diablo).Google Scholar
Thorpe, S. A. 2007 The Turbulent Ocean. Cambridge University Press.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Viswanath, D. & Cvitanović, P. 2009 Stable manifolds and the transition to turbulence in pipe flow. J. Fluid Mech. 627, 215–233.Google Scholar
Waleffe, F. 1995 Hydrodynamic stability and turbulence – beyond transients to a self-sustaining process. Stud. Appl. Maths 95, 319–343.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81, 4140–4143.Google Scholar
Wang, J., Gibson, J. F. & Waleffe, F. 2007 Lower branch coherent state: transition and control. Phys. Rev. Lett. 98, 204501.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.Google Scholar