Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T22:44:57.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of zero-pressure-gradient boundary layers from different tripping conditions

Published online by Cambridge University Press:  22 October 2015

I. Marusic ,
K. A. Chauhan ,
V. Kulandaivelu  and
N. Hutchins
I. Marusic*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
K. A. Chauhan
Affiliation:
School of Civil Engineering, University of Sydney, Sydney, NSW 2006, Australia
V. Kulandaivelu
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
N. Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the spatial evolution of zero-pressure-gradient (ZPG) turbulent boundary layers from their origin to a canonical high-Reynolds-number state. A prime motivation is to better understand under what conditions reliable scaling behaviour comparisons can be made between different experimental studies at matched local Reynolds numbers. This is achieved here through detailed streamwise velocity measurements using hot wires in the large University of Melbourne wind tunnel. By keeping the unit Reynolds number constant, the flow conditioning, contraction and trip can be considered unaltered for a given boundary layer’s development and hence its evolution can be studied in isolation from the influence of inflow conditions by moving to different streamwise locations. Careful attention was given to the experimental design in order to make comparisons between flows with three different trips while keeping all other parameters nominally constant, including keeping the measurement sensor size nominally fixed in viscous wall units. The three trips consist of a standard trip and two deliberately ‘over-tripped’ cases, where the initial boundary layers are over-stimulated with additional large-scale energy. Comparisons of the mean flow, normal Reynolds stress, spectra and higher-order turbulence statistics reveal that the effects of the trip are seen to be significant, with the remnants of the ‘over-tripped’ conditions persisting at least until streamwise stations corresponding to 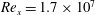$Re_{x}=1.7\times 10^{7}$ and 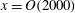$x=O(2000)$ trip heights are reached (which is specific to the trips used here), at which position the non-canonical boundary layers exhibit a weak memory of their initial conditions at the largest scales 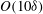$O(10{\it\delta})$, where 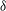${\it\delta}$ is the boundary layer thickness. At closer streamwise stations, no one-to-one correspondence is observed between the local Reynolds numbers (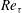$Re_{{\it\tau}}$, 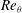$Re_{{\it\theta}}$ or 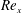$Re_{x}$ etc.), and these differences are likely to be the cause of disparities between previous studies where a given Reynolds number is matched but without account of the trip conditions and the actual evolution of the boundary layer. In previous literature such variations have commonly been referred to as low-Reynolds-number effects, while here we show that it is more likely that these differences are due to an evolution effect resulting from the initial conditions set up by the trip and/or the initial inflow conditions. Generally, the mean velocity profiles were found to approach a constant wake parameter 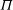${\it\Pi}$ as the three boundary layers developed along the test section, and agreement of the mean flow parameters was found to coincide with the location where other statistics also converged, including higher-order moments up to tenth order. This result therefore implies that it may be sufficient to document the mean flow parameters alone in order to ascertain whether the ZPG flow, as described by the streamwise velocity statistics, has reached a canonical state, and a computational approach is outlined to do this. The computational scheme is shown to agree well with available experimental data.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 379 - 411
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Castillo, L. & Johansson, T. G. 2002 The effects of the upstream conditions on a low Reynolds number turbulent boundary layer with zero pressure gradient. J. Turbul. 3 (31), 1–19.Google Scholar
Castillo, L. & Walker, D. 2002 Effect of upstream conditions on the outer flow of turbulent boundary layers. AIAA J. 40 (7), 1292–1299.CrossRefGoogle Scholar
Chauhan, K. A. & Nagib, H. M. 2008 On the development of wall-bounded turbulent flows. In IUTAM Symposium on Computational Physics and New Perspectives in Turbulence, pp. 183–189. Springer.Google Scholar
Chauhan, K. A., Nagib, H. M. & Monkewitz, P. A. 2007 On the composite logarithmic profile in zero pressure gradient turbulent boundary layers. In 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, vol. 1, pp. 532–549.Google Scholar
Chauhan, K. A., Nagib, H. M. & Monkewitz, P. A. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.Google Scholar
Chin, C. C., Hutchins, N., Ooi, A. S. H. & Marusic, I. 2009 Use of direct numerical simualtion (DNS) data to investigate spatial resolution issues in measurements of wall-bounded turbulence. Meas. Sci. Technol. 20, 115401.Google Scholar
Coles, D. E. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1, 191–226.CrossRefGoogle Scholar
Coles, D. E.1962 The turbulent boundary layer in a compressible fluid. Appendix A: A manual of experimental boundary-layer practice for low-speed flow. Tech. Rep. R-403-PR. USAF The Rand Corporation.Google Scholar
DeGraff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Erm, L. P.1988 Low-Reynolds-number turbulent boundary layers. PhD thesis, The University of Melbourne, Melbourne, Australia.Google Scholar
Erm, L. P. & Joubert, P. N. 1991 Low-Reynolds-number turbulent boundary layer. J. Fluid Mech. 230, 1–44.CrossRefGoogle Scholar
Freymuth, P. 1967 Feedback control theory for constant-temperature hot-wire anemometers. Rev. Sci. Instrum. 38 (5), 677–681.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.Google Scholar
George, W. K. & Castillo, L. 1997 Zero pressure gradient turbulent boundary layer. Appl. Mech. Rev. 50, 689–729.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hutchins, N. 2012 Caution: tripping hazards. J. Fluid Mech. 710, 1–4.Google Scholar
Hutchins, N., Ganapathisubramani, B. & Marusic, I. 2004 Dominant spanwise Fourier modes, and the existence of very large scale coherence in turbulent boundary layers. In 15th Australasian Fluid Mechanics Conference, Sydney, Australia, AFMS.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Hutchins, N., Monty, J. P., Hultmark, M. & Smits, A. J. 2015 A direct measure of the frequency response of hot-wire anemometers: temporal resolution issues in wall-bounded turbulence. Exp. Fluids 56 (1), 1–18.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 101–136.Google Scholar
Inoue, M., Mathis, R., Marusic, I. & Pullin, D. I. 2012 Inner-layer intensities for the flat-plate turbulent boundary layer combining a predictive wall-model with large-eddy simulations. Phys. Fluids 24 (7), 075102.Google Scholar
Johansson, G. & Castillo, L. 2001 LDA measurements in turbulent boundary layers with zero pressure gradient. In Proc. 2nd Int. Symp. Turbulent Shear Flow Phenomena, Stockholm, Sweden.Google Scholar
Jones, M. B.1998 Evolution and structure of sink flow turbulent boundary layers. PhD thesis, The University of Melbourne, Melbourne, Australia.Google Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 1995 The effect of aspect ratio and divergence on the turbulence structure of boundary layers. In Proceedings of the 12th Australasian Fluid Mech. Conf., Sydney, Australia, pp. 436–439.Google Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 2001 Evolution and structure of sink-flow turbulent boundary layers. J. Fluid Mech. 428, 1–27.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.Google Scholar
Klebanoff, P. S. & Diehl, Z. W.1951 Some features of artificially thickened fully developed turbulent boundary layers with zero pressure gradient. Tech. Rep. 2475. DTIC Document.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. J. Fluids Engng 132 (9), 094001.Google Scholar
Kulandaivelu, V.2012 Evolution of zero pressure gradient turbulent boundary layers from different initial conditions. PhD thesis, University of Melbourne.Google Scholar
Lee, M. K. & Moser, R. D. 2015 Direct numerical simulation of a turbulent channel flow up to $Re_{{\it\tau}}=5200$ . J. Fluid Mech. 744, 395–415.Google Scholar
Lewkowicz, A. K. 1982 An improved universal wake function for turbulent boundary layers and some of its consequences. Z. Flugwiss. Weltraumforsch. 6, 261–266.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5, 407–417.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31, 418–428.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010b Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues. Phys. Fluids 22 (6), 065103.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-contained high Reynolds-number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19, 115101.CrossRefGoogle Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20, 105102.Google Scholar
Moses, H. L.1964 The behavior of turbulent boundary layers in adverse pressure gradients. Tech. Rep. 73. Gas Turbine Lab. MIT.Google Scholar
Musker, A. J. 1979 Explicit expression for the smooth wall velocity distribution in a turbulent boundary layer. AIAA J. 17 (6), 655–657.Google Scholar
Nagano, Y., Tagawa, M. & Tsuji, T. 1993 Effects of adverse pressure gradients on mean flows and turbulence statistics in a boundary layer. In Turbulent Shear Flows 8, pp. 7–21. Springer.Google Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365, 755–770.Google Scholar
Nickels, T. B. 2004 Inner scaling for wall-bounded flows subject to large pressure gradients. J. Fluid Mech. 521, 217–239.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the $k_{1}^{-1}$ law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.Google Scholar
Österlund, J. M.1999 Experimental studies of zero-pressure gradient turbulent boundary layer flow. PhD thesis, Royal Institute of Technolgy, Stockholm, Sweden.Google Scholar
Palumbo, D. 2013 The variance of convection velocity in the turbulent boundary layer and its effect on coherence length. J. Sound Vib. 332 (15), 3692–3705.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 198, 361–388.CrossRefGoogle Scholar
Perry, A. E., Marusic, I. & Jones, M. B. 2002 On the streamwise evolution of turbulent boundary layers in arbitrary pressure gradients. J. Fluid Mech. 461, 61–91.Google Scholar
Perry, A. E., Marusic, I. & Li, J. D. 1994 Wall turbulence closure based on classical similarity laws and the attached eddy hypothesis. Phys. Fluids 6 (2), 1024–1035.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.Google Scholar
Schlichting, H. 1960 Boundary-layer Theory. McGraw-Hill.Google Scholar
Seo, J., Castillo, L., Johansson, T. G. & Hangan, H. 2004 Reynolds stress in turbulent boundary layers at high Reynolds number. J. Turbul. 5, 1–13.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Talluru, K. M., Kulandaivelu, V., Hutchins, N. & Marusic, I. 2014 A calibration technique to correct sensor drift issues in hot-wire anemometry. Meas. Sci. Technol. 25 (10), 105304.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015 Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.Google Scholar