Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-04T19:23:16.973Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of the scalar dissipation rate downstream of a concentrated line source in turbulent channel flow

Published online by Cambridge University Press:  15 May 2014

E. Germaine ,
L. Mydlarski  and
L. Cortelezzi
E. Germaine
Affiliation:
Department of Mechanical Engineering, McGill University, Montréal, Québec, H3A 0C3, Canada
L. Mydlarski*
Affiliation:
Department of Mechanical Engineering, McGill University, Montréal, Québec, H3A 0C3, Canada
L. Cortelezzi
Affiliation:
Department of Mechanical Engineering, McGill University, Montréal, Québec, H3A 0C3, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dissipation rate, 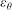$\varepsilon _{\theta }$, of a passive scalar (temperature in air) emitted from a concentrated source into a fully developed high-aspect-ratio turbulent channel flow is studied. The goal of the present work is to investigate the return to isotropy of the scalar field when the scalar is injected in a highly anisotropic manner into an inhomogeneous turbulent flow at small scales. Both experiments and direct numerical simulations (DNS) were used to study the downstream evolution of 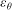$\varepsilon _{\theta }$ for scalar fields generated by line sources located at the channel centreline 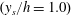$(y_s/h = 1.0)$ and near the wall $(y_s/h = 0.17)$. The temperature fluctuations and temperature derivatives were measured by means of a pair of parallel cold-wire thermometers in a flow at 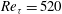$Re_{\tau } = 520$. The DNS were performed at $Re_{\tau } = 190$ using a spectral method to solve the continuity and Navier–Stokes equations, and a flux integral method (Germaine, Mydlarski & Cortelezzi, J. Comput. Phys., vol. 174, 2001, pp. 614–648) for the advection–diffusion equation. The statistics of the scalar field computed from both experimental and numerical data were found to be in good agreement, with certain discrepancies that were attributable to the difference in the Reynolds numbers of the two flows. A return to isotropy of the small scales was never perfectly observed in any region of the channel for the downstream distances studied herein. However, a continuous decay of the small-scale anisotropy was observed for the scalar field generated by the centreline line source in both the experiments and DNS. The scalar mixing was found to be more rapid in the near-wall region, where the experimental results exhibited low levels of small-scale anisotropy. However, the DNS, which were performed at lower 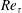$Re_{\tau }$, showed that persistent anisotropy can also exist near the wall, independently of the downstream location. The role of the mean velocity gradient in the production of 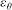$\varepsilon _{\theta }$ (and therefore anisotropy) in the near-wall region was highlighted.

JFM classification

Mixing: Mixing Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 749 , 25 June 2014 , pp. 227 - 274
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Matsuo, Y. 2001 Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. J. Fluid. Eng. - T. ASME 123, 382–393.Google Scholar
Abe, H., Kawamura, H. & Matsuo, Y. 2004 Surface heat-flux fluctuations in a turbulent channel flow up to ${Re}_{\tau }= 1020$ with ${Pr} = 0.025$ and 0.71. Intl J. Heat Fluid Flow 25, 404–419.CrossRefGoogle Scholar
Anselmet, F., Djeridi, H. & Fulachier, L. 1994 Joint statistics of a passive scalar and its dissipation in turbulent flows. J. Fluid Mech. 280, 173–197.Google Scholar
Anselmet, F., Djeridi, H. & Fulachier, L. 1997 Simultaneous measurements of temperature and its dissipation using pairs of parallel cold wires. Exp. Fluids 23, 177–186.CrossRefGoogle Scholar
Antonia, R. A. & Browne, L. W. B. 1986 Anisotropy of the temperature dissipation in a turbulent wake. J. Fluid Mech. 163, 393–403.Google Scholar
Antonia, R. A. & Kim, J. 1994 A numerical study of local isotropy of turbulence. Phys. Fluids 6, 834–841.Google Scholar
Antonia, R. A., Kim, J. & Browne, L. W. B. 1991 Some characteristics of small-scale turbulence in a turbulent duct flow. J. Fluid Mech. 233, 369–388.CrossRefGoogle Scholar
Antonia, R. A. & Mi, J. 1993 Temperature dissipation in a turbulent round jet. J. Fluid Mech. 250, 531–551.CrossRefGoogle Scholar
Bakosi, J., Franzese, P. & Boybeyi, Z. 2007 Probability density function modeling of scalar mixing from concentrated sources in turbulent channel flow. Phys. Fluids 19, 115106.Google Scholar
Balsara, D. S. 2001 Divergence-free adaptive mesh refinement for magnetohydrodynamics. J. Comput. Phys. 174, 614–648.Google Scholar
Boppana, V. B. L., Xie, Z. T. & Castro, I. P. 2012 Large-eddy simulation of dispersion from line sources in a turbulent channel flow. Flow Turbul. Combust. 88, 311–342.CrossRefGoogle Scholar
Brethouwer, G., Boersma, B. J., Pourquie, M. & Nieuwstadt, F. T. M. 1999 Direct numerical simulation of turbulent mixing of a passive scalar in pipe flow. Eur. J. Mech. (B/Fluids) 18, 739–756.Google Scholar
Brethouwer, G., Hunt, J. C. R. & Nieuwstadt, F. T. M. 2003 Micro-structure and Lagrangian statistics of the scalar field with a mean gradient in isotropic turbulence. J. Fluid Mech. 474, 193–225.Google Scholar
Chamecki, M., Meneveau, C. & Parlange, M. B. 2008 A hybrid spectral/finite-volume algorithm for large-eddy simulation of scalars in the atmospheric boundary layer. Boundary-Layer Meteorol. 128, 473–484.Google Scholar
Chung, M. K. & Kyong, N. H. 1989 Measurement of turbulent dispersion behind a fine cylindrical heat source in a weakly sheared flow. J. Fluid Mech. 205, 171–193.Google Scholar
Clyne, J., Mininni, P., Norton, A. & Rast, M. 2007 Interactive desktop analysis of high resolution simulations: application to turbulent plume dynamics and current sheet formation. New J. Phys. 9, 301.CrossRefGoogle Scholar
Clyne, J. & Rast, M.2005 A prototype discovery environment for analyzing and visualizing terascale turbulent fluid flow simulations. In EProc. Visualization and Data Analysis 2005 pp. 284–294.Google Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22, 469–473.Google Scholar
Corrsin, S. 1952 Heat transfer in isotropic turbulence. J. Appl. Phys. 23, 113–118.Google Scholar
Corrsin, S.1953 Remarks on turbulent heat transfer Proceedings of Iowa Thermodynamics Symposium, State University of Iowa, Iowa City pp. 5–30.Google Scholar
Costa-Patry, E. & Mydlarski, L. 2008 Mixing of two thermal fields emitted from line sources in turbulent channel flow. J. Fluid Mech. 609, 349–375.Google Scholar
Dahm, W. J. A. & Buch, K. A. 1989 Lognormality of the scalar dissipation pdf in turbulent flows. Phys. Fluids A 1, 1290–1293.Google Scholar
Danaila, L., Antonia, R. A. & Burattini, P. 2012 Comparison between kinetic energy and passive scalar energy transfer in locally homogeneous isotropic turbulence. Physica D 241, 224–231.Google Scholar
Danaila, L., Zhou, T., Anselmet, F. & Antonia, R. A. 2000 Calibration of a temperature dissipation probe in decaying grid turbulence. Exp. Fluids 28, 45–50.Google Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2005 Scalar dissipation rate and dissipative anomaly in isotropic turbulence. J. Fluid Mech. 532, 199–216.Google Scholar
Fackrell, J. E. & Robins, A. G. 1982 Concentration fluctuations and fluxes in plumes from point sources in a turbulent boundary layer. J. Fluid Mech. 117, 1–26.Google Scholar
Galantucci, L. & Quadrio, M. 2010 Very fine near-wall structures in turbulent scalar mixing. Intl J. Heat Fluid Flow 31, 499–506.CrossRefGoogle Scholar
Germaine, E., Mydlarski, L. & Cortelezzi, L. 2013 3DFLUX: a high-order fully three-dimensional flux integral solver for the scalar transport equation. J. Comput. Phys. 240, 121–144.Google Scholar
Gibson, J. F.2010 Channelflow: a spectral Navier–Stokes simulator in C++. Tech. Rep. University of New Hampshire.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gonzalez, M. 2000 Study of the anisotropy of a passive scalar field at the level of dissipation. Phys. Fluids 12, 2302–2310.Google Scholar
Gonzalez, M. & Paranthoën, P. 2003 On the role of vorticity in the microstructure of a passive scalar field. Phys. Fluids 16, 219–221.Google Scholar
Gurvich, A. S. & Yaglom, A. M. 1967 Breakdown of eddies and probability distributions for small-scale turbulence. Phys. Fluids 10, 59–65.Google Scholar
Holzer, M. & Siggia, E. D. 1994 Turbulent mixing of a passive scalar. Phys. Fluids 6, 1820–1837.Google Scholar
Hussain, A. K. M. F. & Reynolds, W. C. 1975 Measurements in fully developed turbulent channel flow. Trans. ASME J. Fluids Engng 97, 568–578.Google Scholar
Incropera, F. P., De Witt, D. P., Bergman, T. L. & Lavine, A. S. 2007 Fundamentals of Heat and Mass Transfer. 6th edn John Wiley and Sons Inc.Google Scholar
Jayesh,  & Warhaft, Z. 1992 Probability distribution, conditional dissipation, and transport of passive temperature fluctuations in grid-generated turbulence. Phys. Fluids A 4, 2292–2307.CrossRefGoogle Scholar
Johansson, A. V. & Wikström, P. M. 1999 DNS and modelling of passive scalar transport in turbulent channel flow with a focus on scalar dissipation rate modelling. Flow Turbul. Combust. 63, 223–245.Google Scholar
Kailasnath, P., Sreenivasan, K. R. & Saylor, J. R. 1993 Conditional scalar dissipation rates in turbulent wakes, jets, and boundary layers. Phys. Fluids A 5, 3207–3215.Google Scholar
Karnik, U. & Tavoularis, S. 1989 Measurements of heat diffusion from a continuous line source in a uniformly sheared turbulent flow. J. Fluid Mech. 202, 233–261.Google Scholar
Kawamura, H., Ohsaka, K., Abe, H. & Yamamoto, K. 1998 DNS of turbulent heat transfer in channel flow with low to medium-high Prandtl number fluid. Intl J. Heat Fluid Flow 19, 482–491.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kolmogorov, A. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kozuka, M., Seki, Y. & Kawamura, H. 2009 DNS of turbulent heat transfer in a channel flow with a high spatial resolution. Intl J. Heat Fluid Flow 30, 514–524.Google Scholar
LaRue, J. C. & Libby, P. A. 1981 Thermal mixing layer downstream of half-heated turbulence grid. Phys. Fluids 24, 597–603.Google Scholar
Lavertu, R. A. & Mydlarski, L. 2005 Scalar mixing from a concentrated source in turbulent channel flow. J. Fluid Mech. 528, 135–172.Google Scholar
Lemay, J. & Benaïssa, A. 2001 Improvement of cold-wire response for measurement of temperature dissipation. Exp. Fluids 31, 347–356.Google Scholar
Lepore, J. & Mydlarski, L. 2011 Lateral dispersion from a concentrated line source in turbulent channel flow. J. Fluid Mech. 678, 417–450.CrossRefGoogle Scholar
Li, S. & Li, H. 2004 A novel approach of divergence-free reconstruction for adaptive mesh refinement. J. Comput. Phys. 199, 1–15.Google Scholar
Livescu, D., Jaberi, F. A. & Madnia, C. K. 2000 Passive-scalar wake behind a line source in grid turbulence. J. Fluid Mech. 416, 117–149.Google Scholar
Lockwood, F. C. & Moneib, H. A. 1980 Fluctuating temperature measurements in a heated round free jet. Combust. Sci. Technol. 22, 63–81.Google Scholar
Lumley, J. L. 1978 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.Google Scholar
Ma, B. K. & Warhaft, Z. 1986 Some aspects of the thermal mixing layer in grid turbulence. Phys. Fluids 29, 3114–3120.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to ${R}e= 590$ . Phys. Fluids 11, 943–945.Google Scholar
Mydlarski, L. 2003 Mixed velocity-passive scalar statistics in high-Reynolds-number turbulence. J. Fluid Mech. 475, 173–203.Google Scholar
Mydlarski, L., Danaila, L. & Lavertu, R. A.2007 Isotropy of the temperature field downstream of a line source in turbulent channel flow. Advances in Turbulence XI, Proceedings of the 11th EUROMECH European Turbulence Conference, vol. 117, pp. 500–502.Google Scholar
Obukhov, A. M. 1949 Structure of the temperature field in a turbulent current. Izv. Akad. Nauk SSSR Ser. Geogr. Geofiz 13, 58–69.Google Scholar
Paranthoën, P., Fouari, A., Dupont, A. & Lecordier, J. C. 1988 Dispersion measurements in turbulent flows (boundary layer and plane jet). Intl J. Heat Mass Transfer 31, 153–165.Google Scholar
Pope, S. B. & Ching, E. S. C. 1993 Stationary probability density functions: an exact result. Phys. Fluids 5, 1529–1531.Google Scholar
Prasad, R. R. & Sreenivasan, K. R. 1990 Quantitative three-dimensional imaging and the structure of passive scalar fields in fully turbulent flows. J. Fluid Mech. 216, 1–34.Google Scholar
Raupach, M. R. & Legg, B. J. 1983 Turbulent dispersion from an elevated line source: measurements of wind-concentration moments and budgets. J. Fluid Mech. 136, 111–137.Google Scholar
Rosset, L., Paranthoën, P., Lecordier, J. C. & Gonzalez, M. 2001 Anisotropy of a thermal field at dissipative scales in the case of small-scale injection. Phys. Fluids 13, 3729–3737.CrossRefGoogle Scholar
Schumacher, J. & Sreenivasan, K. R. 2005 Statistics and geometry of passive scalars in turbulence. Phys. Fluids 17, 1–9.Google Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.Google Scholar
Schwertfirm, F. & Manhart, M. 2007 DNS of passive scalar transport in turbulent channel flow at high Schmidt numbers. Intl J. Heat Fluid Flow 28, 1204–1214.Google Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.CrossRefGoogle Scholar
Sinai, Y. G. & Yakhot, V. 1989 Limiting probability distributions of a passive scalar in a random velocity field. Phys. Rev. Lett. 63, 1962–1964.CrossRefGoogle Scholar
Sreenivasan, K. R. 1984 On the scaling of the turbulence energy dissipation rate. Phys. Fluids 27, 1048–1051.Google Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent shear flows. Proc. R. Soc. Lond. A 434, 165–182.Google Scholar
Sreenivasan, K. R., Antonia, R. A. & Danh, H. Q. 1977 Temperature dissipation fluctuations in a turbulent boundary layer. Phys. Fluids 20, 1238–1249.Google Scholar
Stapountzis, H., Sawford, B. L., Hunt, J. C. R. & Britter, R. E. 1986 Structure of the temperature field downwind of a line source in grid turbulence. J. Fluid Mech. 165, 401–424.CrossRefGoogle Scholar
Su, L. K. & Clemens, N. T. 2003 The structure of fine-scale scalar mixing in gas-phase planar turbulent jets. J. Fluid Mech. 488, 1–29.Google Scholar
Sutton, J. A. & Driscoll, J. F. 2013 Measurements and statistics of mixture fraction and scalar dissipation rates in turbulent non-premixed jet flames. Combust. Flame 160, 1767–1778.Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Parts 1–4. Proc. R. Soc. Lond. A 151, 421–478.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press, Cambridge, MA.Google Scholar
Thomson, D. J. 1996 The second-order moment structure of dispersing plumes and puffs. J. Fluid Mech. 320, 305–329.Google Scholar
Thoroddsen, S. T. & Van Atta, C. W. 1996 Experiments on density-gradient anisotropies and scalar dissipation of turbulence in a stably stratified fluid. J. Fluid Mech. 322, 383–409.Google Scholar
Tong, C. & Warhaft, Z. 1995 Passive scalar dispersion and mixing in a turbulent jet. J. Fluid Mech. 292, 1–38.Google Scholar
Uberoi, M. S. & Corrsin, S.1952 Diffusion of heat from a line source in isotropic turbulence Tech. Rep. Nat. Adv. Comm. Aero.Google Scholar
Van Atta, C. 1991 Local isotropy of the smallest scales of turbulent scalar and velocity fields. Proc. R. Soc. Lond. A 434, 139–147.Google Scholar
Vrieling, A. J. & Nieuwstadt, F. T. M. 2003 Turbulent dispersion from nearby point sources – interference of the concentration statistics. Atmos. Environ. 37, 4493–4506.Google Scholar
Warhaft, Z. 1984 The interference of thermal fields from line sources in grid turbulence. J. Fluid Mech. 144, 363–387.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.Google Scholar
Wyngaard, J. C. 1969 Spatial resolution of the vorticity meter and other hot-wire arrays. J. Phys. E: Sci. Instrum. 2, 983–987.Google Scholar
Yeung, P. K., Xu, S. & Sreenivasan, K. R. 2002 Schmidt number effects on turbulent transport with uniform mean scalar gradient. Phys. Fluids 14, 4178–4191.Google Scholar
Zhou, T., Antonia, R. A., Lasserre, J. J., Coantic, M. & Anselmet, F. 2003 Transverse velocity and temperature derivative measurements in grid turbulence. Exp. Fluids 34, 449–459.Google Scholar