Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T07:28:14.807Z Has data issue: false hasContentIssue false
  • English
  • Français

The evolution of the initial flow structures of a highly under-expanded circular jet

Published online by Cambridge University Press:  20 May 2019

Huan-Hao Zhang Open the ORCID record for Huan-Hao Zhang [Opens in a new window] ,
Nadine Aubry ,
Zhi-Hua Chen ,
Wei-Tao Wu  and
Sha Sha
Huan-Hao Zhang
Affiliation:
Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China
Nadine Aubry
Affiliation:
Department of Mechanical and Industrial Engineering, Northeastern University, Boston, MA 02115, USA
Zhi-Hua Chen*
Affiliation:
Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China
Wei-Tao Wu*
Affiliation:
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China
Sha Sha
Affiliation:
Beijing Institute of Electronic System Engineering, Beijing 100854, China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

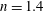The three-dimensional flow characteristics of the compressible vortex ring generated by under-expanded circular jets with two typical pressure ratios, i.e. $n=1.4$ (moderate) and 4.0 (high), are investigated numerically with the use of large-eddy simulations. Our results illustrate that these two pressure ratios correspond to different shock structures (shock cell and Mach disc, respectively) within the jet. These two typical types of flow structures and characteristics are discussed and validated with experiments, and the different generation mechanisms of the secondary vortex rings are compared. Moreover, detailed information about the evolution of the secondary vortex ring, primary vortex ring and turbulence transition features, including the radial and azimuthal modes, is investigated. The geometric features and mixing effects of the jets are also explored.

JFM classification

Compressible Flows: Gas dynamics Wakes/Jets: Jets Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 305 - 331
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Archer, P. J., Thomas, T. G. & Coleman, G. N. 2008 Direct numerical simulation of vortex ring evolution from the laminar to the early turbulent regime. J. Fluid Mech. 598, 201–226.Google Scholar
Arakeri, J. H., Das, D., Krothapalli, A. & Lourenco, L. 2004 Vortex ring formation at the open end of a shock tube: a particle image velocimetry study. Phys. Fluids 16, 1008–1019.Google Scholar
Berger, M. & Colella, P. 1989 Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 82, 64–84.Google Scholar
Brouillette, M., Tardif, J. & Gauthier, E. 1995 Experimental study of shock-generated vortex rings. In Shock Waves @ Marseille IV, pp. 361–366. Springer.Google Scholar
Brouillette, M. & Hebert, C. 1997 Propagation and interaction of shock-generated vortices. Fluid Dyn. Res. 21, 159–169.Google Scholar
Colonius, T., Lele, S. K. & Moin, P. 1994 Scattering of sound waves by a compressible vortex: numerical simulations and analytical solutions. J. Fluid Mech. 260, 271–298.Google Scholar
Deiterding, R., Cirak, F., Mauch, S. P. & Meiron, D. I. 2007 A virtual test facility for simulating detonation- and shock-induced deformation and fracture of thin flexible shells. Intl J. Multiscale Comput. Engng 5, 47–69.Google Scholar
Donaldson, C. D. & Snedeker, R. S. 1971 A study of free jet impingement. Part 1. Mean properties of free and impinging jets. J. Fluid Mech. 45, 281–319.Google Scholar
Hamzehloo, A. & Aleiferis, P. G. 2016 Gas dynamics and flow characteristics of highly turbulent under-expanded hydrogen and methane jets under various nozzle pressure ratios and ambient pressures. Intl J. Hydrogen Energy 41, 6544–6566.Google Scholar
Hillier, R. 1991 Computation of shock wave diffraction at a ninety degrees convex edge. Shock Waves 1, 89–98.Google Scholar
Hill, D. J. & Pullin, D. I. 2004 Hybrid tuned center-difference-WENO method for large eddy simulations in the presence of strong shocks. J. Comput. Phys. 194, 435–454.Google Scholar
Hill, D. J., Pantano, C. & Pullin, D. I. 2006 Large-eddy simulation and multiscale modeling of a Richtmyer–Meshkov instability with re-shock. J. Fluid Mech. 557, 29–61.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proc. 1988 Summer Program of the Center for Turbulence Research, pp. 193–207.Google Scholar
Ishii, R., Fujimoto, H., Hatta, N. & Umeda, Y. 1999 Experimental and numerical analysis of circular pulse jets. J. Fluid Mech. 392, 129–153.Google Scholar
Kitajima, S., Iwamoto, J. & Tamura, E. 2009 A study on the behavior of shock wave and vortex ring discharged from a pipe. In 10th International Conference on Fluid Control, Measurements, and Visualization, August 17–21, Moscow, Russia.Google Scholar
Kosovic, B., Pullin, D. I. & Samtaney, R. 2002 Subgrid-scale modeling for large-eddy simulations of compressible turbulence. Phys. Fluids 14, 1511–1522.Google Scholar
Li, H. Z., Jiang, X. H., Wang, Y. & Guo, Z. Q. 2015 Intermediate Ballistics. Beijing Institute of Technology Press.Google Scholar
Lombardini, M., Hill, D. J., Pullin, D. I. & Meiron, D. I. 2011 Atwood ratio dependence of Richtmyer–Meshkov flows under reshock conditions using large-eddy simulations. J. Fluid Mech. 670, 439–480.Google Scholar
Lundgren, T. S. 1982 Strained spiral vortex model for turbulent fine structure. Phys. Fluids 25, 2193–2203.Google Scholar
Maeno, K., Kaneta, T., Morioka, T. & Honma, H. 2005 Pseudo-schlieren CT measurement of three-dimensional flow phenomena on shock waves and vortices discharged from open ends. Shock Waves 14, 239–249.Google Scholar
Mariani, R., Quinn, M. K. & Kontis, K. 2013 A note on the generation of a compressible vortex rings using helium as driver gas. Proc. Inst. Mech. Engrs Part G 227, 1637–1645.Google Scholar
Matsuda, T., Vuorinen, V., Yu, J., Tirunagari, S., Kaario, O., Larmi, M., Duwig, C. & Boersma, B. J. 2013 Large-eddy simulation of highly under-expanded transient gas jets. Phys. Fluids 25, 016101.Google Scholar
Misra, A. & Pullin, D. I. 1997 A vortex-based subgrid stress model for large-eddy simulation. Phys. Fluids 9, 2443–2454.Google Scholar
Minota, T. 1998 Shock/vortex interaction in a flow field behind a shock wave emitted from a shock-tube. In Proceedings of the 2nd International Workshop on Shock Wave/Vortex Interaction, pp. 149–160. International Shock Wave Institute.Google Scholar
Murugan, T. & Das, D. 2010 Characteristics of counter-rotating vortex rings formed ahead of a compressible vortex ring. Exp. Fluids 49, 1247–1261.Google Scholar
Murugan, T., De, S., Dora, C. L., Das, D. & Prem Kumar, P. 2013 A study of the counter rotating vortex rings interacting with the primary vortex ring in shock tube generated flows. Fluid Dyn. Res. 45, 025506.Google Scholar
Pantano, C., Deiterding, R., Hill, D. J. & Pullin, D. I. 2007 A low numerical dissipation patch based adaptive mesh refinement method for large-eddy simulation of compressible flows. J. Comput. Phys. 221, 63–87.Google Scholar
Pullin, D. I. 2000 A vortex-based model for the subgrid flux of a passive scalar. Phys. Fluids 12, 2311–2319.Google Scholar
Ran, H. & Colonius, T. 2009 Numerical simulation of the sound radiated from a turbulent vortex ring. Aeroacoustics 8, 317–336.Google Scholar
Ran, H.2004 Numerical study of the dynamics and sound generation of a turbulent vortex ring. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar
Saffman, P. 1978 The number of waves on unstable vortex rings. J. Fluid Mech. 84, 625–639.Google Scholar
Widnall, S. & Tsai, C. 1977 The instability of the thin vortex rings of constant vorticity. Phil. Trans. R. Soc. Lond. A 287, 273–305.Google Scholar
Zare-Behtash, H., Kontis, K. & Gongora-Orozco, N. 2008a Experimental investigation of compressible vortex loops. Phys. Fluids 20, 126105.Google Scholar
Zare-Behtash, H., Kontis, K. & Takayama, K.2008b Compressible vortex loops studies in a shock tube with various exit geometries. AIAA Paper 2008-362.Google Scholar
Zare-Behtash, H., Kontis, K., Gongora-Orozco, N. & Takayama, H. 2009a Compressible vortex loops: effect of nozzle geometry. Intl J. Heat Fluid Flow 30, 561–576.Google Scholar
Zare-Behtash, H., Gongora-Orozco, N. & Kontis, K. 2009b Global visualization and quantification of compressible vortex loops. J. Vis. 12, 233–240.Google Scholar
Zare-Behtash, H., Kontis, K., Gongora-Orozco, N. & Takayama, K. 2010 Shock wave-induced vortex loops emanating from nozzles with singular corners. Exp. Fluids 49, 1005–1019.Google Scholar
Zhang, H. H., Chen, Z. H., Jiang, X. H. & Li, B. M. 2011 Numerical investigations on the thrust augmentation mechanisms of ejectors driven by pulse detonation engines. Combust. Sci. Technol. 183, 1069–1082.Google Scholar
Zhang, H. H., Chen, Z. H., Jiang, X. H. & Li, H. Z. 2013 Investigations on the exterior flow fields and the efficiency of the muzzle brake. J. Mech. Sci. Technol. 27, 95–101.Google Scholar
Zhang, H. H., Chen, Z. H., Li, B. M. & Jiang, X. H. 2014 The secondary vortex rings of a supersonic under-expanded circular jet with low pressure ratio. Eur. J. Mech. (B/Fluids) 46, 172–180.Google Scholar
Zhang, H. H., Chen, Z. H., Jiang, X. H. & Huang, Z. G. 2015 The starting flow structures and evolution of a supersonic planar jet. Comput. Fluids 114, 98–109.Google Scholar
Zhang, H. H., Chen, Z. H., Guo, Z. Q. & Sun, X. H. 2017 Characteristic behavior of shock pattern and primary vortex loop of a supersonic square jet. Intl J. Heat Mass Transfer 115, 347–363.Google Scholar
Zhang, H. H., Chen, Z. H., Guo, Z. Q., Zheng, C. & Xue, D. W. 2018 Numerical investigation on the three-dimensional flow characteristics of unsteady subsonic elliptic jet. Comput. Fluids 160, 78–92.Google Scholar