Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T15:49:17.877Z Has data issue: false hasContentIssue false
  • English
  • Français

Evaporation with the formation of chains of liquid bridges

Published online by Cambridge University Press:  05 January 2018

C. Chen ,
P. Joseph ,
S. Geoffroy ,
M. Prat  and
P. Duru Open the ORCID record for P. Duru [Opens in a new window]
C. Chen
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS - Toulouse, France
P. Joseph
Affiliation:
LAAS-CNRS, CNRS, Université de Toulouse, Toulouse, France
S. Geoffroy
Affiliation:
Laboratoire Matériaux et Durabilité des Constructions (LMDC), UPS-INSA, Université de Toulouse, Toulouse, France
M. Prat
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS - Toulouse, France
P. Duru*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS - Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

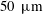The objective of the present work is to study the drying of a quasi-two-dimensional model porous medium, hereafter called the micromodel, initially filled with a pure liquid. The micromodel consists of cylinders measuring $50~\unicode[STIX]{x03BC}\text{m}$ in both height and diameter, radially arranged as a set of neighbouring spirals and sandwiched between two horizontal flat plates. As drying proceeds, air invades the pore space and elongated liquid films trapped by capillary forces form along the spirals. These films consist of ‘chains’ of liquid bridges connecting neighbouring cylinders. They provide hydraulic connectivity between the central bulk liquid cluster and the external rim of the cylinder pattern, where evaporation takes place during a first constant-evaporation-rate drying stage. The first goal of the present paper is to describe experimentally the phase distribution during drying, notably the evolution of liquid films, which controls the evaporation kinetics (e.g. the depinning of the films from the external rim signals the end of the constant-evaporation-rate period). Then, a viscocapillary model for the drying process is presented. It is based on numerical simulations of a liquid film capillary shape and viscous flow within a film. The model shows a reasonably good agreement with the experimental data. Thus, the present study is a step towards direct modelling of the effect of films on the drying of more complex porous media (e.g. packing of beads) and should be of interest for multiphase flow applications in porous media, involving transport within liquid films.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Liquid bridges Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 837 , 25 February 2018 , pp. 703 - 728
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Guangdong Key Laboratory for Biomedical Measurements and Ultrasound Imaging, Department of Biomedical Engineering, Shenzhen University, China.

References

Altshuller, A. P. & Cohen, I. R. 1960 Application of diffusion cells to production of known concentration of gaseous hydrocarbons. Analyt. Chem. 32 (7), 802–810.Google Scholar
Armstrong, R. T. & Berg, S. 2013 Interfacial velocities and capillary pressure gradients during haines jumps. Phys. Rev. E 88 (4), 043010.Google Scholar
Berg, S., Ott, H., Klapp, S. A., Schwing, A., Neiteler, R., Brussee, N., Makurat, A., Leu, L., Enzmann, F., Schwarz, J. O. et al. 2013 Real-time 3d imaging of haines jumps in porous media flow. Proc. Natl Acad. Sci. USA 110 (10), 3755–3759.Google Scholar
Beverley, K. J., Clint, J. H. & Fletcher, P. D. I. 1999 Evaporation rates of pure liquids measured using a gravimetric technique. Phys. Chem. Chem. Phys. 1 (1), 149–153.Google Scholar
Brakke, K. A. 1992 The surface evolver. Exp. Math. 1 (2), 141–165.Google Scholar
Ceaglske, N. H. & Hougen, O. A. 1937 Drying granular solids. Ind. Engng Chem. 29 (7), 805–813.Google Scholar
Cejas, C. M., Hough, L. A., Frétigny, C. & Dreyfus, R.2016 Effect of granular packing geometry on evaporation. ArXiv preprint, arXiv:1601.04584.Google Scholar
Chauvet, F.2009 Effet des films liquides en évaporation. PhD thesis, Institut National Polytechnique de Toulouse.Google Scholar
Chauvet, F., Duru, P., Geoffroy, S. & Prat, M. 2009 Three periods of drying of a single square capillary tube. Phys. Rev. Lett. 103 (12), 124502.Google Scholar
Chauvet, F., Cazin, S., Duru, P. & Prat, M. 2010a Use of infrared thermography for the study of evaporation in a square capillary tube. Intl J. Heat Mass Transfer 53 (9), 1808–1818.Google Scholar
Chauvet, F., Duru, P. & Prat, M. 2010b Depinning of evaporating liquid films in square capillary tubes: influence of corners roundedness. Phys. Fluids 22 (11), 112113.Google Scholar
Chen, C.2016 Evaporation au sein de systèmes microfluidiques: des structures capillaires à gradient d’ouverture aux spirales phyllotaxiques. PhD thesis, Institut National des Sciences Appliquées de Toulouse.Google Scholar
Chen, C., Duru, P., Joseph, P., Geoffroy, S. & Prat, M. 2017 Control of evaporation by geometry in capillary structures: from confined pillar arrays in a gap radial gradient to phyllotaxy inspired geometry. Sci. Rep. 7, 15110.Google Scholar
Clément, F. & Leng, J. 2004 Evaporation of liquids and solutions in confined geometry. Langmuir 20 (16), 6538–6541.Google Scholar
Coussot, P. 2000 Scaling approach of the convective drying of a porous medium. Eur. Phys. J. B 15 (3), 557–566.Google Scholar
Cummings, G. A. McD. & Ubbelohde, A. R. 1953 Collision diameters of flexible hydrocarbon molecules in the vapour phase: the ‘hydrogen effect’. J. Chem. Soc. (Resumed) 3751–3755.Google Scholar
Douady, S. & Couder, Y. 1992 Phyllotaxis as a physical self-organized growth process. Phys. Rev. Lett. 68 (13), 2098.Google Scholar
Elliott, R. W. & Watts, H. 1972 Diffusion of some hydrocarbons in air: a regularity in the diffusion coefficients of a homologous series. Can. J. Chem. 50 (1), 31–34.Google Scholar
Horgue, P., Augier, F., Quintard, M. & Prat, M. 2012 A suitable parametrization to simulate slug flows with the volume-of-fluid method. Comptes Rendus Méc. 340 (6), 411–419.Google Scholar
Hu, R., Wan, J., Kim, Y. & Tokunaga, T. K. 2017 Wettability impact on supercritical CO2 capillary trapping: pore-scale visualization and quantification. Water Resour. Res. 53 (8), 6377–6394.Google Scholar
Jasper, J. J. & Kring, E. V. 1955 The isobaric surface tensions and thermodynamic properties of the surfaces of a series of n-alkanes, c5 to c18, 1-alkenes, c6 to c16, and of n-decylcyclopentane, n-decylcyclohexane and n-decylbenzene. J. Phys. Chem. 59 (10), 1019–1021.Google Scholar
Jung, M., Brinkmann, M., Seemann, R., Hiller, T., de La Lama, M. S. & Herminghaus, S. 2016 Wettability controls slow immiscible displacement through local interfacial instabilities. Phys. Rev. Fluids 1 (7), 074202.Google Scholar
Keita, E., Koehler, S. A., Faure, P., Weitz, D. A. & Coussot, P. 2016 Drying kinetics driven by the shape of the air/water interface in a capillary channel. Eur. Phys. J. E 39 (2), 1–10.Google Scholar
Kohout, M., Grof, Z. & Štěpánek, F. 2006 Pore-scale modelling and tomographic visualisation of drying in granular media. J. Colloid Interface Sci. 299 (1), 342–351.Google Scholar
Lacey, M., Hollis, C., Oostrom, M. & Shokri, N. 2017 Effects of pore and grain size on water and polymer flooding in micromodels. Energy Fuels 31 (9), 9026–9034.Google Scholar
Laurindo, J. B. & Prat, M. 1998 Numerical and experimental network study of evaporation in capillary porous media. drying rates. Chem. Engng Sci. 53 (12), 2257–2269.Google Scholar
Lehmann, P., Assouline, S. & Or, D. 2008 Characteristic lengths affecting evaporative drying of porous media. Phys. Rev. E 77 (5), 056309.Google Scholar
Lenormand, R., Touboul, E. & Zarcone, C. 1988 Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 189, 165–187.Google Scholar
Lewis, W. K. 1921 The rate of drying of solid materials. Ind. Engng Chem. 13 (5), 427–432.Google Scholar
Lugg, G. A. 1968 Diffusion coefficients of some organic and other vapors in air. Analyt. Chem. 40 (7), 1072–1077.Google Scholar
Machado, A., Bodiguel, H., Beaumont, J., Clisson, G. & Colin, A. 2016 Extra dissipation and flow uniformization due to elastic instabilities of shear-thinning polymer solutions in model porous media. Biomicrofluidics 10 (4), 043507.Google Scholar
Prat, M. 2007 On the influence of pore shape, contact angle and film flows on drying of capillary porous media. Intl J. Heat Mass Transfer 50 (7), 1455–1468.Google Scholar
Prat, M. 2011 Pore network models of drying, contact angle, and film flows. Chem. Engng Technol. 34 (7), 1029–1038.Google Scholar
Raeini, A. Q., Blunt, M. J. & Bijeljic, B. 2012 Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 231 (17), 5653–5668.Google Scholar
Ransohoff, T. C. & Radke, C. J. 1988 Laminar flow of a wetting liquid along the corners of a predominantly gas-occupied noncircular pore. J. Colloid Interface Sci. 121 (2), 392–401.Google Scholar
Reid, R. C., Prausnitz, J. M. & Sherwood, T. K. 1987 The Properties of Gases and Liquids, 3rd edn. McGraw-Hill.Google Scholar
Scheel, M., Seemann, R., Brinkmann, M., Di Michiel, M., Sheppard, A., Breidenbach, B. & Herminghaus, S. 2008a Morphological clues to wet granular pile stability. Nat. Mater. 7 (3), 189–193.Google Scholar
Scheel, M., Seemann, R., Brinkmann, M., Di Michiel, M., Sheppard, A. & Herminghaus, S. 2008b Liquid distribution and cohesion in wet granular assemblies beyond the capillary bridge regime. J. Phys. 20 (49), 494236.Google Scholar
Scherer, G. W. 1990 Theory of drying. J. Amer. Ceramic Soc. 73 (1), 3–14.Google Scholar
Shahidzadeh-Bonn, N., Azouni, A. & Coussot, P. 2007 Effect of wetting properties on the kinetics of drying of porous media. J. Phys. 19 (11), 112101.Google Scholar
Shaw, T. M. 1987 Drying as an immiscible displacement process with fluid counterflow. Phys. Rev. Lett. 59 (15), 1671–1674.Google Scholar
Sherwood, T. K. 1929a The drying of solids–i. Ind. Engng Chem. 21 (1), 12–16.Google Scholar
Sherwood, T. K. 1929b The drying of solids–ii. Ind. Engng Chem. 21 (10), 976–980.Google Scholar
Shokri, N., Lehmann, P. & Or, D. 2010 Liquid-phase continuity and solute concentration dynamics during evaporation from porous media: pore-scale processes near vaporization surface. Phys. Rev. E 81 (4), 046308.Google Scholar
Singh, K., Menke, H., Andrew, M., Lin, Q., Rau, C., Blunt, M. J. & Bijeljic, B. 2017a Dynamics of snap-off and pore-filling events during two-phase fluid flow in permeable media. Sci. Rep. 7, 5192.Google Scholar
Singh, K., Scholl, H., Brinkmann, M., Di Michiel, M., Scheel, M., Herminghaus, S. & Seemann, R. 2017b The role of local instabilities in fluid invasion into permeable media. Sci. Rep. 7, 444.Google Scholar
Tsimpanogiannis, I. N., Yortsos, Y. C., Poulou, S., Kanellopoulos, N. & Stubos, A. K. 1999 Scaling theory of drying in porous media. Phys. Rev. E 59 (4), 4353.Google Scholar
Van Brakel, J. 1980 Mass transfer in convective drying. In Advances in Drying, vol. 1 (ed. Mujumdar, A. S.), pp. 217–267. Hemisphère Publishing Corporation.Google Scholar
Vargaftik, N. B. 1975 Handbook of Physical Properties of Liquids and Gases-Pure Substances and Mixtures. Hemisphere Publishing Corporation.Google Scholar
Vorhauer, N., Wang, Y. J., Karaghani, A., Tsotsas, E. & Prat, M. 2015 Drying with formation of capillary rings in a model porous medium. Trans. Porous Med. 110 (2), 197–223.Google Scholar
Yang, F., Griffa, M., Bonnin, A., Mokso, R., Bella, C., Münch, B., Kaufmann, R. & Lura, P. 2015 Visualization of water drying in porous materials by x-ray phase contrast imaging. J. Microsc. 261 (1), 88–104.Google Scholar
Yiotis, A. G., Salin, D., Tajer, E. S. & Yortsos, Y. C. 2012a Analytical solutions of drying in porous media for gravity-stabilized fronts. Phys. Rev. E 85 (4), 046308.Google Scholar
Yiotis, A. G., Salin, D., Tajer, E. S. & Yortsos, Y. C. 2012b Drying in porous media with gravity-stabilized fronts: experimental results. Phys. Rev. E 86 (2), 026310.Google Scholar
Yiotis, A. G., Boudouvis, A. G., Stubos, A. K., Tsimpanogiannis, I. N. & Yortsos, Y. C. 2003 Effect of liquid films on the isothermal drying of porous media. Phys. Rev.  E 68 (3), 037303.Google Scholar
Yiotis, A. G., Boudouvis, A. G., Stubos, A. K., Tsimpanogiannis, I. N. & Yortsos, Y. C. 2004 Effect of liquid films on the drying of porous media. AIChE J. 50 (11), 2721–2737.Google Scholar