Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T15:56:29.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimating wall-shear-stress fluctuations given an outer region input

Published online by Cambridge University Press:  09 January 2013

Romain Mathis ,
Ivan Marusic ,
Sergei I. Chernyshenko  and
Nicholas Hutchins
Romain Mathis*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia Laboratoire de Mécanique de Lille, UMR CNRS 8107, 59655 Villeneuve d’Ascq, France
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Sergei I. Chernyshenko
Affiliation:
Department of Aeronautics, Imperial College, London SW7 2AZ, UK
Nicholas Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

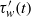A model for the instantaneous wall-shear-stress distribution is presented for zero-pressure-gradient turbulent boundary layers. The model, based on empirical and theoretical considerations, is able to reconstruct a statistically representative fluctuating wall-shear-stress time-series, ${ \tau }_{w}^{\ensuremath{\prime} } (t)$, using only the low-frequency content of the streamwise velocity measured in the logarithmic region, away from the wall. Results, including spectra and second-order moments, show that the model is capable of successfully capturing Reynolds number trends as observed in other studies.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 163 - 180
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Alfredsson, P. H., Johansson, A. V., Haritonidis, J. H. & Eckelmann, H. 1988 The fluctuating wall-shear stress and the velocity-field in the viscous sublayer. Phys. Fluids 31 (5), 1026–1033.Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.Google Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23, 061701.CrossRefGoogle Scholar
Brand, A., Lacy, J. R., Hsu, H., Hoover, D., Gladding, S. & Stacey, M. T. 2010 Wind-enhanced resuspension in the shallow waters of South San Francisco Bay: mechanisms and potential implications for cohesive sediment transport. J. Geophys. Res. – Oceans 115, 1–15.CrossRefGoogle Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary-layer. Phys. Fluids 20 (10), S243–S251.Google Scholar
Bruun, H. H. 1995 Hot-wire Anemometry. Oxford University Press.Google Scholar
Chauhan, K. A., Ng, H. C. H. & Marusic, I. 2010 Empirical mode decomposition and Hilbert transforms for analysis of oil-film interferograms. Meas. Sci. Technol 21, 105404.CrossRefGoogle Scholar
Chew, Y. T., Khoo, B. C., Lim, C. P. & Teo, C. J. 1998 Dynamic response of a hot-wire anemometer. Part II: a flush-mounted hot-wire and hot-film probes for wall shear stress measurments. Meas. Sci. Technol. 9, 764–778.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1: vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2: long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32, 245–311.Google Scholar
Grant, S. B. & Marusic, I. 2012 Crossing turbulent boundaries: interfacial flux in environmental flows. Environ. Sci. Technol. 45, 1443–1453.Google Scholar
Grant, W. D. & Madsen, O. S. 1986 The continental-shelf bottom boundary layer. Annu. Rev. Fluid Mech. 18, 265–305.Google Scholar
Grinvald, D. & Nikora, V. 1988 Rechnaya Turbulentsiya (River Turbulence). Hydrometeoizdat (in Russian).Google Scholar
Hambleton, W. T., Hutchins, N. & Marusic, I. 2006 Simultaneous orthogonal-plane particular image velocimetry measurements in turbulent boundary layer. J. Fluid Mech. 560, 53–64.Google Scholar
Hunt, J. C. R. & Durbin, P. A. 1999 Perturbed vortical layers and shear sheltering. Fluid Dyn. Res. 24, 375–404.Google Scholar
Hunt, J. C. R., Eames, I., Westerwel, J., Davidson, P. A., Voropayev, S., Fernando, J. & Braza, M. 2010 Thin shear layers – the key to turbulence structure? J. Hydraul Environ. Res. 4, 75–82.CrossRefGoogle Scholar
Hunt, J. C. R. & Morrison, J. F. 2000 Eddy structure in turbulent boundary layers. Eur. J. Mech. (B/Fluids) 19, 673–694.CrossRefGoogle Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. P. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145, 273–306.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google ScholarPubMed
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high Reynolds number turbulent boundary layer. J. Fluid Mech. 673, 255–285.Google Scholar
Hutchins, N., Nickels, T., Marusic, I. & Chong, M. S. 2009 Spatial resolution issues in hot-wire anemometry. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Inoue, M., Mathis, R., Marusic, I. & Pullin, D. I. 2012 Inner-layer intensities for the flat-plate turbulent boundary layer combining a predictive wall-model with large-eddy simulations. Phys. Fluids 24 (7), 075102.Google Scholar
Jacobs, R. G. & Durbin, P. A. 1998 Shear sheltering and the continuous spectrum of the Orr-Sommerfeld equation. Phys. Fluids 10 (8), 2006–2011.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME: J. Fluids Engng 132, 094001.Google Scholar
Klewicki, J. C., Metzger, M. M., Kelner, E. & Thurlow, E. M. 1995 Viscous sublayer flow visualizations at ${\mathit{Re}}_{\theta } = 1\hspace{0.167em} 500\hspace{0.167em} 000$. Phys. Fluids 7, 857–963.Google Scholar
Komminaho, J. & Skote, M. 2002 Reynolds stress budgets in Couette and boundary layer flows. Flow Turbul. Combust. 68, 167–192.CrossRefGoogle Scholar
Kreplin, H. P. & Eckelmann, H. 1979 Propagation of perturbations in the viscous sublayer and adjacent wall region. J. Fluid Mech. 95, 305–322.Google Scholar
Kulandaivelu, V. 2012 Evolution and structure of zero pressure gradient turbulent boundary layer. PhD thesis, The University of Melbourne, Melbourne.Google Scholar
Kunkel, G. J. & Marusic, I. 2003 An approximate amplitude attenuation correction for hot-film shear stress sensors. Exp. Fluids 34, 285–290.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Lenaers, P., Li, Q., Brethouwer, G., Schlatter, P. & Örlü, R. 2012 Rare backflow and extreme wall-normal velocity fluctuations in near-wall turbulence. Phys. Fluids 24, 035110.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5, 407–417.Google Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure angle in wall turbulence. Phys. Rev. Lett. 99, 114501.Google Scholar
Marusic, I. & Hutchins, N. 2008 Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow Turbul. Combust. 81, 115–130.CrossRefGoogle Scholar
Marusic, I., Kunkel, G. J. & Porté-Agel, F. 2001 Experimental study of wall boundary conditions for large-eddy simulation. J. Fluid Mech. 446, 309–320.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010b Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.CrossRefGoogle ScholarPubMed
Marusic, I., Mathis, R. & Hutchins, N. 2011 A wall shear stress predictive model. J. Phys.: Conf. Ser. 318 (1), 012003. Proceeding of the 13th European Turblence Conference (ETC13), Warsaw, Poland, 12–15 September 2011.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010c Wall-bounded turbulent flows: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011a A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011b The relationship between the velocity skewness and the amplitude modulation of the small scale by the large-scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.CrossRefGoogle Scholar
Mathis, R., Monty, J., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes and channel flows. Phys. Fluids 21 (11), 111703.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13, 692–701.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-consistent high-Reynolds-number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19, 115101.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20, 105102.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.CrossRefGoogle Scholar
Nagib, H., Smits, A., Marusic, I. & Alfredsson, P. H. 2009 ICET – International collaboration on experiments in turbulence: coordinated measurements in high Reynolds number turbulent boundary layers from three wind tunnels. In Bulletin of the 62nd Annual Division of Fluid Dynamics Meeting of the American Physical Society. Minneapolis, Minnesota, USA, Series II, Vol. 54, No. 19 Nov. 2009. American Physical Society.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the ${ k}_{1}^{\ensuremath{-} 1} $ law in high-Reynolds number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.Google Scholar
Örlü, R. & Schlatter, P. 2011 On the fluctuating wall-shear stress in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 23, 021704.CrossRefGoogle Scholar
Österlund, J. M. 1999 Experimental studies of zero pressure-gradient turbulent boundary layer. PhD thesis, KTH, Stockholm.Google Scholar
Prandtl, L. 1905 Uber Flussigkeits bewegung bei sehr kleiner Reibung. In Verhaldlg III Int. Math. Kong. (ed. Krazer, A.). pp. 484–491. Teubner, (also available in translation as: Motion of fluids with very little viscosity).Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Ptasinski, P. K., Boersma, B. J., Nieuwstadt, F. T. M, Hulsen, M. A., Van den Brule, B. H. A. A. & Hunt, J. C. R. 2003 Turbulent channel flow near maximum drag reduction: simulations, experiments and mechanisms. J. Fluid Mech. 490, 251–291.Google Scholar
Rowiński, P., Aberle, J. & Mazurczyk, A. 2005 Shear velocity estimation in hydraulic research. Acta Geophys. Pol. 53 (4), 567–583.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layer. J. Fluid Mech. 659, 116–126.Google Scholar
Schlatter, P. & Örlü, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22 (5), 051704.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory, 8th revised and enlarged edn. Springer.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011a High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Smits, A. J., Monty, J. P., Hultmark, M., Bailey, S. C. C., Hutchins, N. & Marusic, I. 2011b Spatial resolution correction for wall-bounded turbulence measurements. J. Fluid Mech. 676, 41–53.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Zaki, T. & Saha, S. 2009 On shear sheltering and the structure of vortical modes in single- and two-fluid boundary layers. J. Fluid Mech. 626, 111–147.Google Scholar