Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T03:53:43.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Equilibrium structure and diffusion in concentrated hydrodynamically interacting suspensions confined by a spherical cavity

Published online by Cambridge University Press:  11 December 2017

Christian Aponte-Rivera ,
Yu Su  and
Roseanna N. Zia Open the ORCID record for Roseanna N. Zia [Opens in a new window]
Christian Aponte-Rivera
Affiliation:
Robert Frederick Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca NY 14850, USA
Yu Su
Affiliation:
Robert Frederick Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca NY 14850, USA
Roseanna N. Zia*
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The short- and long-time equilibrium transport properties of a hydrodynamically interacting suspension confined by a spherical cavity are studied via Stokesian dynamics simulations for a wide range of particle-to-cavity size ratios and particle concentrations. Many-body hydrodynamic and lubrication interactions between particles and with the cavity are accounted for utilizing recently developed mobility and resistance tensors for spherically confined suspensions (Aponte-Rivera & Zia, Phys. Rev. Fluids, vol. 1(2), 2016, 023301). Study of particle volume fractions in the range 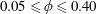$0.05\leqslant \unicode[STIX]{x1D719}\leqslant 0.40$ reveals that confinement exerts a qualitative influence on particle diffusion. First, the mean-square displacement over all time scales depends on the position in the cavity. Additionally, at short times, the diffusivity is anisotropic, with diffusion along the cavity radius slower than diffusion tangential to the cavity wall, due to the anisotropy of hydrodynamic coupling and to confinement-induced spatial heterogeneity in particle concentration. The mean-square displacement is anisotropic at intermediate times as well and, surprisingly, exhibits superdiffusive and subdiffusive behaviours for motion along and perpendicular to the cavity radius respectively, depending on the suspension volume fraction and the particle-to-cavity size ratio. No long-time self-diffusive regime exists; instead, the mean-square displacement reaches a long-time plateau, a result of entropic restriction to a finite volume. In this long-time limit, the higher the volume fraction is, the longer the particles take to reach the long-time plateau, as cooperative rearrangements are required as the cavity becomes crowded. The ordered dynamical heterogeneity seen here promotes self-organization of particles based on their size and self-mobility, which may be of particular relevance in biophysical systems.

JFM classification

Complex Fluids: Colloids Low-Reynolds-number flows: Stokesian dynamics Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , pp. 413 - 450
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlrichs, P., Everaers, R. & Dünweg, B. 2001 Screening of hydrodynamic interactions in semidilute polymer solutions: a computer simulation study. Phys. Rev. E 64 (4 Pt 1), 040501.Google Scholar
Ando, T. & Skolnick, J. 2010 Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc. Natl Acad. Sci. USA 107 (43), 18457–18462.Google Scholar
Aponte-Rivera, C. & Zia, R. N. 2016 Simulation of hydrodynamically interacting particles confined by a spherical cavity. Phys. Rev. Fluids 1 (2), 023301.Google Scholar
Banchio, A. J. & Brady, J. F. 2003 Accelerated Stokesian dynamics: Brownian motion. J. Chem. Phys. 118 (22), 10323–10332.CrossRefGoogle Scholar
Batchelor, G. K. 1976 Brownian diffusion of particles with hydrodynamic interaction. J. Fluid Mech. 74, 1–29.CrossRefGoogle Scholar
Batchelor, G. K. 1982 Sedimentation in a dilute polydisperse system of interacting spheres. Part 1. General theory. J. Fluid Mech. 119, 379–407.Google Scholar
Bhattacharya, S. 2008 Cooperative motion of spheres arranged in periodic grids between two parallel walls. J. Chem. Phys. 128 (7), 074709.CrossRefGoogle ScholarPubMed
Bhattacharya, S., Mishra, C. & Bhattacharya, S. 2010 Analysis of general creeping motion of a sphere inside a cylinder. J. Fluid Mech. 642, 295–328.Google Scholar
Bickel, T. 2007 A note on confined diffusion. Physica A 377 (1), 24–32.CrossRefGoogle Scholar
Brady, J. F. 1994 The long-time self-diffusivity in concentrated colloidal dispersions. J. Fluid Mech. 272, 109–133.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Brangwynne, C. P., Koenderink, G. H., MacKintosh, F. C. & Weitz, D. A. 2008 Cytoplasmic diffusion: molecular motors mix it up. J. Cell Biol. 183 (4), 583–587.Google Scholar
Brangwynne, C. P., Koenderink, G. H., MacKintosh, F. C. & Weitz, D. A. 2009 Intracellular transport by active diffusion. Trends in Cell Biology 19 (9), 423–427.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3–4), 242–251.Google Scholar
Chow, E. & Skolnick, J. 2015 Effects of confinement on models of intracellular macromolecular dynamics. Proc. Natl Acad. Sci. USA 112 (48), 14846–14851.Google Scholar
Colby, R. H. 2010 Structure and linear viscoelasticity of flexible polymer solutions: comparison of polyelectrolyte and neutral polymer solutions. Rheol. Acta 49 (5), 425–442.Google Scholar
Crocker, J. C. & Hoffman, B. D. 2007 Multiple-particle tracking and two-point microrheology in cells. Meth. Cell Biol. 83 (7), 141–178.Google Scholar
Cunningham, E. 1910 On the velocity of steady fall of spherical particles through fluid medium. Proc. R. Soc. Lond. A 83 (563), 357–365.Google Scholar
Daniels, B. R., Masi, B. C. & Wirtz, D. 2006 Probing single-cell micromechanics in vivo: the microrheology of C. elegans developing embryos. Biophys. J. 90 (12), 4712–4719.Google Scholar
Durlofsky, L. & Brady, J. F. 1987 Analysis of the Brinkman equation as a model for flow in porous media. Phys. Fluids 30 (11), 3329–3341.CrossRefGoogle Scholar
Durlofsky, L., Brady, J. F. & Bossis, G. 1987 Dynamic simulation of hydrodynamically interacting particles. J. Fluid Mech. 180, 21–49.Google Scholar
Foss, D. R. & Brady, J. F. 2000 Structure, diffusion and rheology of Brownian suspensions by Stokesian dynamics simulation. J. Fluid Mech. 407, 167–200.CrossRefGoogle Scholar
de Gennes, P. G. 1976 Dynamics of entangled polymer solutions. Part II. Inclusion of hydrodynamic interactions. Macromolecules 9 (4), 594–598.Google Scholar
Golden, A. 2000 Cytoplasmic flow and the establishment of polarity in C. elegans 1-cell embryos. Curr. Opin. Genetics Develop. 10 (4), 414–420.Google Scholar
Golding, I. & Cox, E. 2006 Physical nature of bacterial cytoplasm. Phys. Rev. Lett. 96 (9), 098102.Google Scholar
Gönczy, P. & Rose, L. S.2005 Asymmetric cell division and axis formation in the embryo. In WormBook, The C. elegans Research Community.Google Scholar
González, A., White, J. A., Román, F. L. & Evans, R. 1998 How the structure of a confined fluid depends on the ensemble: hard spheres in a spherical cavity. J. Chem. Phys. 109 (9), 3637–3650.Google Scholar
Henderson, G. P., Gan, L. & Jensen, G. J. 2007 3-D ultrastructure of O. tauri: electron cryotomography of an entire eukaryotic cell. PLoS ONE 2 (8).Google Scholar
Hoh, N. J. & Zia, R. N. 2016a Force-induced diffusion in suspensions of hydrodynamically interacting colloids. J. Fluid Mech. 795, 739–783.Google Scholar
Hoh, N. J. & Zia, R. N. 2016b The impact of probe size on measurements of diffusion in active microrheology. Lab on a Chip 16, 3114–3129.Google Scholar
Hoogerbrugge, P. J. & Koelman, J. M. V. A. 1992 Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Eur. Phys. Lett. 19 (3), 155–160.Google Scholar
Hunter, G. L., Edmond, K. V. & Weeks, E. R. 2014 Boundary mobility controls glassiness in confined colloidal liquids. Phys. Rev. Lett. 112 (21), 218302.Google Scholar
Jaensch, S., Decker, M., Hyman, A. A. & Myers, E. W. 2010 Automated tracking and analysis of centrosomes in early Caenorhabditis elegans embryos. Bioinformatics 26 (12), 13–20.Google Scholar
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.Google Scholar
Jones, R. B. 2009 Dynamics of a colloid in a spherical cavity. In Theoretical Methods for Micro Scale Viscous Flows (ed. Feuillebois, F. & Sellier, A.), chap. 4, pp. 61–104. Transworld Research Network.Google Scholar
Keys, A. S., Iacovella, C. R. & Glotzer, S. C. 2011 Characterizing complex particle morphologies through shape matching: descriptors, applications, and algorithms. J. Comput. Phys. 230 (17), 6438–6463.Google Scholar
Kim, S. H., Park, J. G., Choi, T. M., Manoharan, V. N. & Weitz, D. A. 2014 Osmotic-pressure-controlled concentration of colloidal particles in thin-shelled capsules. Nat. Commun. 5, 3068.Google Scholar
Ladd, A. J. C. 1994 Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.Google Scholar
Ladyzhenskaya, O. A. 1969 The Mathematical Theory of Viscous Incompressible Flow, 2nd edn. Gordon and Breach Science Publishers.Google Scholar
Lau, A. W. C., Hoffman, B. D., Davies, A., Crocker, J. C. & Lubensky, T. C. 2003 Microrheology, stress fluctuations, and active behavior of living cells. Phys. Rev. Lett. 91 (19), 198101.Google Scholar
Leighton, D. & Acrivos, A. 1987 The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.Google Scholar
Marshall, W. F., Straight, A., Marko, J. F., Swedlow, J., Dernburg, A., Belmont, A., Murray, A. W., Agard, D. A. & Sedat, J. W. 1997 Interphase chromosomes undergo constrained diffusional motion in living cells. Current Biology: CB 7 (12), 930–939.Google Scholar
McGuffee, S. R. & Elcock, A. H. 2010 Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput. Biol. 6 (3), e1999694.Google Scholar
Navardi, S. & Bhattacharya, S. 2010 A new lubrication theory to derive far-field axial pressure difference due to force singularities in cylindrical or annular vessels. J. Math. Phys. 51 (4), 043102.Google Scholar
Navardi, S., Bhattacharya, S. & Wu, H. 2015 Stokesian simulation of two unequal spheres in a pressure-driven creeping flow through a cylinder. Comput. Fluids 121, 145–163.Google Scholar
Németh, Z. T. & Löwen, H. 1999 Freezing and glass transition of hard spheres in cavities. Phys. Rev. E 59 (6), 6824–6829.Google Scholar
O’Neill, M. E. & Majumdar, S. R. 1970 Asymmetrical slow viscous fluid motions caused by the translation or rotation of two spheres. Part II. Asymptotic forms of the solutions when the minimum clearance. Z. Angew. Math. Phys. 21, 180–187.Google Scholar
Oseen, C. W. 1927 Neuere Methoden und Ergebnisse in der Hydrodynamik. Akademische Verlagsgesellschaft M.B.H.Google Scholar
Peng, Y., Chen, W., Fischer, T. M., Weitz, D. A. & Tong, P. 2009 Short-time self-diffusion of nearly hard spheres at an oil–water interface. J. Fluid Mech. 618, 243–261.Google Scholar
Percus, J. K. & Yevick, G. J. 1958 Analysis of classical statistical mechanics by means of collective coordinates. Phys. Rev. 110 (1), 1–13.Google Scholar
Rallison, J. M. & Hinch, E. J. 1986 The effect of particle interactions on dynamic light scattering from a dilute suspension. J. Fluid Mech. 167, 131–168.Google Scholar
Shinar, T., Mana, M., Piano, F. & Shelley, M. J. 2011 A model of cytoplasmically driven microtubule-based motion in the single-celled Caenorhabditis elegans embryo. Proc. Natl Acad. Sci. USA 108 (26), 10508–10513.Google Scholar
Sierou, A. & Brady, J. F. 2001 Accelerated Stokesian dynamics simulations. J. Fluid Mech. 448, 115–146.Google Scholar
Snook, I. K. & Henderson, D. 1978 Monte Carlo study of a hard-sphere fluid near a hard wall. J. Chem. Phys. 68 (5), 2134–2139.Google Scholar
Steinhardt, P. J., Nelson, D. R. & Ronchetti, M. 1983 Bond-orientational order in liquids and glasses. Phys. Rev. B 28 (2), 784–805.Google Scholar
Su, Y., Swan, J. W. & Zia, R. N. 2017 Pair mobility functions for rigid spheres in concentrated colloidal dispersions: stresslet and straining motion couplings. J. Chem. Phys. 146, 124903.Google Scholar
Suh, J., Wirtz, D. & Hanes, J. 2003 Efficient active transport of gene nanocarriers to the cell nucleus. Proc. Natl Acad. Sci. USA 100 (7), 3738–3882.Google Scholar
Sun, J. & Weinstein, H. 2007 Toward realistic modeling of dynamic processes in cell signaling: quantification of macromolecular crowding effects. J. Chem. Phys. 127 (15), 155105.Google Scholar
Swan, J. W. & Brady, J. F. 2010 Particle motion between parallel walls: hydrodynamics and simulation. Phys. Fluids 22 (10), 103301.Google Scholar
Swan, J. W. & Brady, J. F. 2011a Anisotropic diffusion in confined colloidal dispersions: the evanescent diffusivity. J. Chem. Phys. 135, 014701.Google Scholar
Swan, J. W. & Brady, J. F. 2011b The hydrodynamics of confined dispersions. J. Fluid Mech. 687, 254–299.Google Scholar
Tabei, S. M. A., Burov, S., Kim, H. Y., Kuznetsov, A., Huynh, T., Jureller, J., Philipson, L. H., Dinner, A. R. & Scherer, N. F. 2013 Intracellular transport of insulin granules is a subordinated random walk. Proc. Natl Acad. Sci. USA 110 (13), 4911–4916.Google Scholar
Teich, E. G., van Anders, G., Klotsa, D., Dshemuchadse, J. & Glotzer, S. C. 2016 Clusters of polyhedra in spherical confinement. Proc. Natl Acad. Sci. USA 113 (6), E669–E678.Google Scholar
Tough, R. J. A. & van den Broeck, C. 1989 Diffusion within a sphere: a non-Gaussian statistical model for particle displacements in a dense colloidal suspension. Physica A 157, 769–796.Google Scholar
Verkman, A. S. 2002 Solute and macromolecule diffusion in cellular aqueous compartments. Trends Biochem. Sci. 27 (1), 27–33.Google Scholar
Vogel, N., Utech, S., England, G. T., Shirman, T., Phillips, K. R., Koay, N., Burgess, I. B., Kolle, M., Weitz, D. A. & Aizenberg, J. 2015 Color from hierarchy: diverse optical properties of micron-sized spherical colloidal assemblies. Proc. Natl Acad. Sci. USA 112 (35), 10845–10850.Google Scholar
Wachsmuth, M., Waldeck, W. & Langowski, J. 2000 Anomalous diffusion of fluorescent probes inside living cell nuclei investigated by spatially-resolved fluorescence correlation spectroscopy. J. Molecular Biol. 298 (4), 677–689.Google Scholar
Weber, S. C. & Brangwynne, C. P. 2015 Inverse size scaling of the nucleolus by a concentration-dependent phase transition. Current Biology 25, 1–6.Google Scholar
Weber, S. C., Theriot, J. A. & Spakowitz, A. J. 2010 Subdiffusive motion of a polymer composed of subdiffusive monomers. Phys. Rev. E 82 (1), 1–11.CrossRefGoogle ScholarPubMed
Weeks, E. R., Crocker, J. C., Levitt, A. C., Schofield, A. & Weitz, D. A. 2000 Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science 287 (5453), 627–631.Google Scholar
Weiss, M., Elsner, M., Kartberg, F. & Nilsson, T. 2004 Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 87 (5), 3518–3524.Google Scholar
Wodarz, A. 2002 Establishing cell polarity in development. Nature Cell Biol. 4, 39–44.Google Scholar
Zia, R. N., Swan, J. W. & Su, Y. 2015 Pair mobility functions for rigid spheres in concentrated colloidal dispersions: force, torque, translation, and rotation. J. Chem. Phys. 143, 224901.Google Scholar

Aponte-Rivera et al. supplementary movie

Stokesian dynamics simulation with full, many-body hydrodynamic and lubrication interactions for a spherically confined, concentrated colloidal suspension. The no-slip and no-flux confining cavity is rigorously modeled via newly developed hydrodynamic mobility couplings. Model can simulate volume fractions up to maximum packing and arbitrary particle-to-cavity size ratio. Shown here is equilibrium diffusion for 30% volume fraction and particles 10% of cavity size.”

Download Aponte-Rivera et al. supplementary movie(Video)
Video 17.7 MB
Supplementary material: PDF

Aponte-Rivera et al. supplementary material

Supplementary figure

Download Aponte-Rivera et al. supplementary material(PDF)
PDF 2.2 MB