Article contents
Equilibrium radial positions of neutrally buoyant spherical particles over the circular cross-section in Poiseuille flow
Published online by Cambridge University Press: 26 January 2017
Abstract
An experimental study of the inertial migration of neutrally buoyant spherical particles suspended in the Poiseuille flow through circular tubes has been conducted at Reynolds numbers 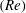 $(Re)$ from 100 to 1100 for particle-to-tube diameter ratios of
$(Re)$ from 100 to 1100 for particle-to-tube diameter ratios of 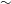 ${\sim}$0.1. The distributions of particles in the tube cross-section were measured at various distances from the tube inlet and the radial probability function of particles was calculated. At relatively high
${\sim}$0.1. The distributions of particles in the tube cross-section were measured at various distances from the tube inlet and the radial probability function of particles was calculated. At relatively high 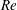 $Re$, the radial probability function was found to have two peaks, corresponding to the so-called Segre–Silberberg annulus and the inner annulus, the latter of which was first reported experimentally by Matas et al. (J. Fluid Mech. vol. 515, 2004, pp. 171–195) to represent accumulation of particles at smaller radial positions than the Segre–Silberberg annulus. They assumed that the inner annulus would be an equilibrium position of particles, where the resultant lateral force on the particles disappears, similar to the Segre–Silberberg annulus. The present experimental study showed that the fraction of particles observed on the Segre–Silberberg annulus increased and the fraction on the inner annulus decreased further downstream, accompanying an outward shift of the inner annulus towards the Segre–Silberberg annulus and a decrease in its width. These results suggested that if the tubes were long enough, the inner annulus would disappear such that all particles would be focused on the Segre–Silberberg annulus for
$Re$, the radial probability function was found to have two peaks, corresponding to the so-called Segre–Silberberg annulus and the inner annulus, the latter of which was first reported experimentally by Matas et al. (J. Fluid Mech. vol. 515, 2004, pp. 171–195) to represent accumulation of particles at smaller radial positions than the Segre–Silberberg annulus. They assumed that the inner annulus would be an equilibrium position of particles, where the resultant lateral force on the particles disappears, similar to the Segre–Silberberg annulus. The present experimental study showed that the fraction of particles observed on the Segre–Silberberg annulus increased and the fraction on the inner annulus decreased further downstream, accompanying an outward shift of the inner annulus towards the Segre–Silberberg annulus and a decrease in its width. These results suggested that if the tubes were long enough, the inner annulus would disappear such that all particles would be focused on the Segre–Silberberg annulus for 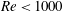 $Re<1000$. At the cross-section nearest to the tube inlet, particles were absent in the peripheral region close to the tube wall including the expected Segre–Silberberg annulus position for
$Re<1000$. At the cross-section nearest to the tube inlet, particles were absent in the peripheral region close to the tube wall including the expected Segre–Silberberg annulus position for 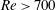 $Re>700$. In addition, the entry length after which radial migration has fully developed was found to increase with increasing
$Re>700$. In addition, the entry length after which radial migration has fully developed was found to increase with increasing 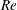 $Re$, in contrast to the conventional estimate. These results may be related to the developing flow in the tube entrance region where the radial force profile would be different from that of the fully developed Poiseuille flow and there may not be an equilibrium position corresponding to the Segre–Silberberg annulus.
$Re$, in contrast to the conventional estimate. These results may be related to the developing flow in the tube entrance region where the radial force profile would be different from that of the fully developed Poiseuille flow and there may not be an equilibrium position corresponding to the Segre–Silberberg annulus.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 42
- Cited by



