Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-08T05:36:59.429Z Has data issue: false hasContentIssue false
  • English
  • Français

The equilibrium dynamics and statistics of gravity–capillary waves

Published online by Cambridge University Press:  18 February 2015

W. Kendall Melville  and
Alexey V. Fedorov
W. Kendall Melville*
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92093-0213, USA
Alexey V. Fedorov
Affiliation:
Department of Geology and Geophysics, Yale University, 210 Whitney Avenue, PO Box 208109, New Haven, CT 06520, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent field observations and modelling of breaking surface gravity waves suggest that air-entraining breaking is not sufficiently dissipative of surface gravity waves to balance the dynamics of wind-wave growth and nonlinear interactions with dissipation for the shorter gravity waves of 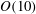$O(10)$  cm wavelength. Theories of parasitic capillary waves that form at the crest and forward face of shorter steep gravity waves have shown that the dissipative effects of these waves may be one to two orders of magnitude greater than the viscous dissipation of the underlying gravity waves. Thus the parasitic capillaries may provide the required dissipation of the short wind-generated gravity waves. This has been the subject of speculation and conjecture in the literature. Using the nonlinear theory of Fedorov & Melville (J. Fluid Mech., vol. 354, 1998, pp. 1–42), we show that the dissipation due to the parasitic capillaries is sufficient to balance the wind input to the short gravity waves over some range of wave ages and wave slopes. The range of gravity wave lengths on which these parasitic capillary waves are dynamically significant approximately corresponds to the range of short gravity waves that Cox & Munk (J. Mar. Res., vol. 13, 1954, pp. 198–227) found contributed significantly to the mean square slope of the ocean surface, which they measured to be proportional to the wind speed. Here we show that the mean square slope predicted by the theory is proportional to the square of the friction velocity of the wind, 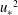${u_{\ast }}^{2}$, for small wave slopes, and approximately 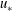$u_{\ast }$ for larger slopes.

JFM classification

Waves/Free-surface Flows: Capillary waves Waves/Free-surface Flows: Surface gravity waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 449 - 466
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banner, M. L. & Morison, R. P. 2010 Refined source terms in wind wave models with explicit wave breaking prediction. Part 1: model framework and validation against field data. Ocean Model. 33, 177–189.CrossRefGoogle Scholar
Banner, M. L. & Peirson, W. 2007 Wave breaking onset and strength for two-dimensional deep-water wave groups. J. Fluid Mech. 585, 93–115.CrossRefGoogle Scholar
Banner, M. L. & Phillips, O. M. 1974 On the incipient breaking of small-scale waves. J. Fluid Mech. 65, 647–656.CrossRefGoogle Scholar
Bréon, F. M. & Henriot, N. 2006 Spaceborne observations of ocean glint reflectance and modeling of wave slope distributions. J. Geophys. Res. 111, C06005.Google Scholar
Cox, C. & Munk, W. 1954 Statistics of the sea surface derived from sun glitter. J. Mar. Res. 13, 198–227.Google Scholar
Deike, L., Popinet, S. & Melville, W. K. 2015 Capillary effects on breaking. J. Fluid Mech. (in press).CrossRefGoogle Scholar
Donelan, M. A., Haus, B. K., Reul, N., Plant, W. J., Stiassnie, M., Graber, H. C., Brown, O. B. & Saltzman, E. S. 2004 On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 31, L18306.CrossRefGoogle Scholar
Drazen, D. A., Melville, W. K. & Lenain, L. 2008 Inertial scaling of dissipation in unsteady breaking waves. J. Fluid Mech. 611, 307–332.CrossRefGoogle Scholar
Duncan, J. H., Philomin, V., Behres, M. & Kimmel, J. 1994 The formation of spilling breaking water waves. Phys. Fluids 6, 2558–2560.CrossRefGoogle Scholar
Duncan, J. H., Qiao, H., Philomin, V. & Wenz, A. 1999 Gentle spilling breakers: crest profile evolution. J. Fluid Mech. 379, 191–222.CrossRefGoogle Scholar
Fedorov, A. V. & Melville, W. K. 1998 Nonlinear gravity–capillary waves with forcing and dissipation. J. Fluid Mech. 354, 1–42.CrossRefGoogle Scholar
Fedorov, A. V. & Melville, W. K. 2009 A model of strongly forced wind waves. J. Phys. Oceanogr. 39, 2502–2522.CrossRefGoogle Scholar
Fedorov, A. V., Melville, W. K. & Rozenberg, A. 1998 Experimental and numerical study of parasitic capillary waves. Phys. Fluids 10, 1315–1323.CrossRefGoogle Scholar
Grare, L., Peirson, W., Branger, H., Walker, J., Giovangeli, J.-P. & Makin, V. K. 2013 Growth and dissipation of wind-forced, deep water waves. J. Fluid Mech. 722, 5–50.CrossRefGoogle Scholar
Hogan, S. J. 1980 Some effects of surface tension on steep water waves. Part 2. J. Fluid Mech. 96, 417–445.CrossRefGoogle Scholar
Hogan, S. J. 1981 Some effects of surface tension on steep water waves. Part 3. J. Fluid Mech. 110, 381–410.CrossRefGoogle Scholar
Janssen, P. 2004 The Interaction of Ocean Waves and Wind. Cambridge University Press.CrossRefGoogle Scholar
Komen, G. J., Cavaleri, L., Donelan, M., Hasselmann, K., Hasselmann, S. & Janssen, P. A. E. M. 1994 Dynamics and Modelling of Ocean Waves. Cambridge University Press.CrossRefGoogle Scholar
Large, W. G. & Pond, S. 1981 Open ocean momentum flux measurements in moderate to strong winds. J. Phys. Oceanogr. 11, 324–336.2.0.CO;2>CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1992 Capillary rollers and bores. J. Fluid Mech. 240, 659–679.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1995 Parasitic capillary waves: a direct calculation. J. Fluid Mech. 301, 79–107.CrossRefGoogle Scholar
Melville, W. K. 1994 Energy dissipation by breaking waves. J. Phys. Oceanogr. 24, 2041–2049.2.0.CO;2>CrossRefGoogle Scholar
Miles, J. W. 1959 On the generation of surface waves by shear flows. Part 2. J. Fluid Mech. 6, 568–582.CrossRefGoogle Scholar
Miles, J. W. 1993 Surface wave generation revisited. J. Fluid Mech. 256, 427–441.CrossRefGoogle Scholar
Munk, W. 2009 An inconvenient sea truth: spread, steepness, and skewness of surface slopes. Annu. Rev. Mar. Sci. 1, 377–415.CrossRefGoogle ScholarPubMed
Perlin, M., Jiang, L., Lin, H. J. & Schultz, W. W. 1999 Unsteady ripple generation on steep gravity–capillary waves. J. Fluid Mech. 386, 281–304.Google Scholar
Perlin, M. & Schultz, W. W. 2000 Capillary effects on surface waves. Annu. Rev. Fluid Mech. 32, 241–274.CrossRefGoogle Scholar
Phillips, O. M. 1977 Dynamics of the Upper Ocean. Cambridge University Press.Google Scholar
Phillips, O. M. 1985 Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J. Fluid Mech. 156, 505–531.CrossRefGoogle Scholar
Pizzo, N. E. & Melville, W. K. 2013 Vortex generation by deep-water breaking waves. J. Fluid Mech. 734, 198–218.CrossRefGoogle Scholar
Plant, W. J. 1982 A relation between wind stress and wave slope. J. Geophys. Res. C 87, 767–793.CrossRefGoogle Scholar
Romero, L., Melville, W. K. & Kleiss, J. M. 2012 Spectral energy dissipation due to surface wave breaking. J. Phys. Oceanogr. 42, 1421–1444.CrossRefGoogle Scholar
Ruvinsky, K. D., Feldstein, F. I. & Freidman, G. I. 1991 Numerical simulations of the quasi-stationary stage of ripple excitation by steep gravity–capillary waves. J. Fluid Mech. 230, 339–353.CrossRefGoogle Scholar
Sutherland, P. & Melville, W. K. 2013 Field measurements and scaling of ocean surface wave-breaking statistics. Geophys. Res. Lett. 40, 3074–3079.CrossRefGoogle Scholar
Townsend, A. A. 1972 Flow in a deep turbulent boundary layer over a surface distorted by water waves. J. Fluid Mech. 55, 719–735.CrossRefGoogle Scholar
Tsai, W.-T. & Hung, L.-P. 2010 Enhanced energy dissipation by parasitic capillaries on short gravity–capillary waves. J. Phys. Oceanogr. 40, 2435–2450.CrossRefGoogle Scholar
Yang, D., Meneveau, C. & Shen, L. 2013 Dynamic modelling of sea-surface roughness for large-eddy simulation of wind over ocean wavefield. J. Fluid Mech. 726, 62–99.CrossRefGoogle Scholar
Zhang, X. 2002 Enhanced dissipation of short gravity and gravity capillary waves due to parasitic capillaries. Phys. Fluids 14, L81–L84.CrossRefGoogle Scholar