Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T03:00:40.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Entrainment and structure of negatively buoyant jets

Published online by Cambridge University Press:  25 January 2021

L. Milton-McGurk Open the ORCID record for L. Milton-McGurk [Opens in a new window] ,
N. Williamson Open the ORCID record for N. Williamson [Opens in a new window] ,
S.W. Armfield ,
M.P. Kirkpatrick Open the ORCID record for M.P. Kirkpatrick [Opens in a new window]  and
K.M. Talluru Open the ORCID record for K.M. Talluru [Opens in a new window]
L. Milton-McGurk*
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
N. Williamson
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
S.W. Armfield
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
M.P. Kirkpatrick
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
K.M. Talluru
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

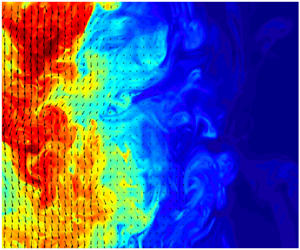
Turbulent negatively buoyant jets occur when the buoyancy of a jet directly opposes its momentum, and will decelerate until its mean momentum is reduced to zero. Here, the flow reverses direction and, for an axisymmetric flow originating from a round inlet, returns annularly towards the source, mixing with the opposing fluid and forming a fountain. This investigation focuses on the initial stage of the flow, before the return flow is established. Data are obtained experimentally using two-dimensional particle image velocimetry and planar laser induced fluorescence for saline/freshwater negatively buoyant jets with source Froude number $Fr_o=30$ and Reynolds numbers $5500\lesssim Re_o\lesssim 5900$ at axial locations $18\lesssim z/D\lesssim 30$, and compared to a neutral jet. The development of the mean and turbulence profiles with local $Fr$ are investigated, and it is found that, unlike neutral jets and plumes, the turbulence intensity in negatively buoyant jets does not scale with the mean flow. Additionally, the ratio of widths of the buoyancy and velocity profiles, $\lambda$, increases along the jet. The entrainment coefficient, $\alpha$, was estimated for a negatively buoyant jet, and was found to decrease with local $Fr$, eventually becoming negative, indicating fluid is being ejected from the jet. These observations differ to neutral or buoyant jets and plumes, which approach a constant $\lambda$ and $\alpha$ in the far field. This different behaviour in negatively buoyant jets is a natural consequence of the strongly decelerating mean flow as a result of opposing buoyancy, which is demonstrated in the context of the integral model framework developed by Morton et al. (Proc. R. Soc. Lond. A, vol. 234, no. 1196, 1956, pp. 1–23).

JFM classification

Wakes/Jets: Jets Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A21
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baines, W.D., Turner, J.S. & Campbell, I.H. 1990 Turbulent fountains in an open chamber. J. Fluid Mech. 212, 557–592.CrossRefGoogle Scholar
Berson, F.A. & Baird, G. 1975 A numerical model of cumulonimbus convection generating a protected core. Q. J. R. Meteorol. Soc. 101 (430), 911–928.CrossRefGoogle Scholar
Bloomfield, L.J. & Kerr, R.C. 2000 A theoretical model of a turbulent fountain. J. Fluid Mech. 424, 197–216.CrossRefGoogle Scholar
Burridge, H.C. & Hunt, G.R. 2012 The rise heights of low-and high-Froude-number turbulent axisymmetric fountains. J. Fluid Mech. 691, 392–416.CrossRefGoogle Scholar
Burridge, H.C. & Hunt, G.R. 2016 Entrainment by turbulent fountains. J. Fluid Mech. 790, 407–418.CrossRefGoogle Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2006 The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 547, 137–148.CrossRefGoogle Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2008 On the dynamics of volcanic columns: A comparison of field data with a new model of negatively buoyant jets. J. Volcanol. Geotherm. Res. 178 (1), 94–103.CrossRefGoogle Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2010 The rise and fall of turbulent fountains: a new model for improved quantitative predictions. J. Fluid Mech. 657, 265–284.CrossRefGoogle Scholar
Craske, J., Salizzoni, P. & van Reeuwijk, M. 2017 The turbulent Prandtl number in a pure plume is 3/5. J. Fluid Mech. 822, 774–790.CrossRefGoogle Scholar
Cresswell, R.W. & Szczepura, R.T. 1993 Experimental investigation into a turbulent jet with negative buoyancy. Phys. Fluids A 5 (11), 2865–2878.CrossRefGoogle Scholar
Darisse, A., Lemay, J. & Benaïssa, A. 2015 Budgets of turbulent kinetic energy, Reynolds stresses, variance of temperature fluctuations and turbulent heat fluxes in a round jet. J. Fluid Mech. 774, 95–142.CrossRefGoogle Scholar
Ezzamel, A., Salizzoni, P. & Hunt, G.R. 2015 Dynamical variability of axisymmetric buoyant plumes. J. Fluid Mech. 765, 576–611.CrossRefGoogle Scholar
Fischer, H.B., List, J.E., Koh, C.R., Imberger, J. & Brooks, N.H. 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
Fox, D.G. 1970 Forced plume in a stratified fluid. J. Geophys. Res. 75 (33), 6818–6835.CrossRefGoogle Scholar
Gendron, P.-O., Avaltroni, F. & Wilkinson, K.J. 2008 Diffusion coefficients of several rhodamine derivatives as determined by pulsed field gradient–nuclear magnetic resonance and fluorescence correlation spectroscopy. J. Fluoresc. 18 (6), 1093–1101.Google ScholarPubMed
Hussein, H.J., Capp, S.P. & George, W.K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.Google Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.CrossRefGoogle Scholar
Kaye, N.B. & Hunt, G.R. 2006 Weak fountains. J. Fluid Mech. 558, 319–328.CrossRefGoogle Scholar
McDougall, T.J. 1981 Negatively buoyant vertical jets. Tellus 33 (3), 313–320.CrossRefGoogle Scholar
Milton-McGurk, L., Williamson, N., Armfield, S.W. & Kirkpatrick, M.P. 2020 Experimental investigation into turbulent negatively buoyant jets using combined PIV and PLIF measurements. Intl J. Heat Fluid Flow 82, 108561.CrossRefGoogle Scholar
Mistry, D., Philip, J., Dawson, J.R. & Marusic, I. 2016 Entrainment at multi-scales across the turbulent/non-turbulent interface in an axisymmetric jet. J. Fluid Mech. 802, 690–725.CrossRefGoogle Scholar
Mizushina, T., Ogino, F., Takeuchi, H. & Ikawa, H. 1982 An experimental study of vertical turbulent jet with negative buoyancy. Wärme-Stoffübertrag. 16 (1), 15–21.CrossRefGoogle Scholar
Morton, B.R. 1959 Forced plumes. J. Fluid Mech. 5 (1), 151–163.CrossRefGoogle Scholar
Morton, B.R., Taylor, G.I. & Turner, J.S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A Math. Phys. Sci. 234 (1196), 1–23.Google Scholar
Okwuobi, P.A.C. & Azad, R.S. 1973 Turbulence in a conical diffuser with fully developed flow at entry. J. Fluid Mech. 57 (3), 603–622.CrossRefGoogle Scholar
Panchapakesan, N.R. & Lumley, J.L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.CrossRefGoogle Scholar
Papanicolaou, P.N. & List, E.J. 1988 Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 195, 341–391.CrossRefGoogle Scholar
Papanicolaou, P.N., Papakonstantis, I.G. & Christodoulou, G.C. 2008 On the entrainment coefficient in negatively buoyant jets. J. Fluid Mech. 614, 447–470.CrossRefGoogle Scholar
Pincince, A.B. & List, E.J. 1973 Disposal of brine into an estuary. J. Water Pollut. Control Fed. 45 (11), 2335–2344.Google Scholar
Priestley, C.H.B. & Ball, F.K. 1955 Continuous convection from an isolated source of heat. Q. J. R. Meteorol. Soc. 81 (348), 144–157.CrossRefGoogle Scholar
van Reeuwijk, M. & Craske, J. 2015 Energy-consistent entrainment relations for jets and plumes. J. Fluid Mech. 782, 333–355.CrossRefGoogle Scholar
van Reeuwijk, M., Salizzoni, P., Hunt, G.R. & Craske, J. 2016 Turbulent transport and entrainment in jets and plumes: a DNS study. Phys. Rev. Fluids 1 (7), 074301.CrossRefGoogle Scholar
Singh, R.K. & Azad, R.S. 1995 Structure of turbulence in an incipient-separating axisymmetric flow. J. Fluids Engng 117 (3), 433–438.CrossRefGoogle Scholar
Talluru, K.M., Armfield, S.W., Williamson, N., Kirkpatrick, M.P. & Milton-McGurk, L. 2020 Turbulence structure of neutral and negatively buoyant jets. J. Fluid Mech. (accepted).Google Scholar
Turner, J.S. 1966 Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 26 (4), 779–792.CrossRefGoogle Scholar
Vanderwel, C. & Tavoularis, S. 2014 On the accuracy of PLIF measurements in slender plumes. Exp. Fluids 55 (8), 1801.CrossRefGoogle Scholar
Wang, H. & Law, A.W.-K. 2002 Second-order integral model for a round turbulent buoyant jet. J. Fluid Mech. 459, 397–428.CrossRefGoogle Scholar
Webster, D.R., Roberts, P.J.W. & Ra'ad, L. 2001 Simultaneous DPTV/PLIF measurements of a turbulent jet. Exp. Fluids 30 (1), 65–72.CrossRefGoogle Scholar
Williamson, N., Armfield, S.W. & Lin, W. 2011 Forced turbulent fountain flow behaviour. J. Fluid Mech. 671, 535–558.CrossRefGoogle Scholar
Zehentbauer, F.M., Moretto, C., Stephen, R., Thevar, T., Gilchrist, J.R., Pokrajac, D., Richard, K.L. & Kiefer, J. 2014 Fluorescence spectroscopy of rhodamine 6g: concentration and solvent effects. Spectrochim. Acta A 121, 147–151.CrossRefGoogle ScholarPubMed