Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T01:27:38.107Z Has data issue: false hasContentIssue false
  • English
  • Français

The enhancement of viscous fingering with bidisperse particle suspension

Published online by Cambridge University Press:  07 December 2018

Feng Xu  and
Sungyon Lee Open the ORCID record for Sungyon Lee [Opens in a new window]
Feng Xu
Affiliation:
Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Sungyon Lee*
Affiliation:
Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Viscous fingering is observed experimentally when a bidisperse suspension displaces air inside a Hele-Shaw cell, despite the stabilising viscosity ratio between the invading (suspension) and defending (air) phases. Careful experiments are carried out to characterise this instability by either systematically varying the large-particle concentrations $\unicode[STIX]{x1D719}_{l0}$ at constant total concentrations 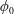$\unicode[STIX]{x1D719}_{0}$, or changing 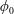$\unicode[STIX]{x1D719}_{0}$ with fixed 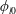$\unicode[STIX]{x1D719}_{l0}$. Leading to the instability, we observe that larger particles consistently enrich the fluid–fluid interface at a faster rate than small particles. This size-dependent enrichment of the interface leads to an earlier onset of the fingering instability for bidisperse suspensions, compared to their monodisperse counterpart of all small particles. In particular, even the small presence of large particles is shown to effectively lower the total particle concentration needed for fingering, compared to the all-small-particle case. We hypothesise that the key mechanism behind this enhanced viscous fingering is the size-dependent nature of shear-induced migration of particles far upstream from the interface. A reduced equilibrium model is derived based on the modified suspension balance model to verify this hypothesis, in reasonable agreement with experiments.

JFM classification

Interfacial Flows (free surface): Fingering instability Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 487 - 509
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alpadydin, E. 2009 Introduction to Machine Learning, 2nd edn. MIT Press.Google Scholar
Altobelli, S. A. & Mondy, L. A. 2002 Hindered flotation functions from nuclear magnetic resonance imaging. J. Rheol. 46, 1341–1352.Google Scholar
Beckwith, T. G. & Marangoni, R. D. 1993 Mechanical Measurements, 5th edn. Addison-Wesley.Google Scholar
Beyea, S. D., Altobelli, S. A. & Mondy, L. A. 2003 Chemically selective NMR imaging of a 3-compoent (solid–solid–liquid) sedimenting syste. J. Magn. Resonance 161, 198–203.Google Scholar
Boyer, F., Guazzelli, E. & Pouliquen, O. 2011 Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.Google Scholar
Chahal, D., Ahmadi, A. & Cheung, K. C. 2012 Improving piezoelectric cell printing accuracy and reliability through neutral buoyancy of suspensions. Biotechnol. Bioengng 109 (11), 2932–2940.Google Scholar
Chapman, B. K.1990 Shear-induced migration phenomena in concentrated suspensions. PhD thesis, University of Notre Dame.Google Scholar
Chow, A. W., Hamlin, R. D. & Ylitalo, C. M. 1995 Size segregation of concentrated bidisperse and polydisperse suspension during tube drawing. In IUTAM Symposium on Hydrodynamic Diffusion of Suspended Particles, pp. 45–50. Colorado University, Boulder, CO.Google Scholar
Connell, J. L., Ritschdorff, E. T., Whiteley, M. & Shear, J. B. 2013 3D printing of microscopic bacterial communities. Proc. Natl Acad. Sci. USA 110 (46), 18380–18385.Google Scholar
Dagois-Bohy, S., Hormozi, S., Guazzelli, E. & Pouliquen, O. 2015 Rheology of dense suspensions of non-colloidal spheres in yield-stress fluids. J. Fluid Mech. 776, R2.Google Scholar
Graham, A. L., Altobelli, S. A., Fukushima, E., Mondy, L. A. & Stephen, T. S. 1991 Note: NMR imaging of shear-induced diffusion and structure in concentrated suspensions undergoing Couette flow. J. Rheol. 135, 191–201.Google Scholar
Homsy, G. M. 1987 Viscous fingering in porous media. Annu. Rev. Fluid Mech. 19, 271–311.Google Scholar
Husband, D. M., Mondy, L. A., Ganani, E. & Graham, A. L. 1994 Direct measurements of shear-induced particle migration in suspensions of bimodal spheres. Rheol. Acta 33, 185–192.Google Scholar
Karnis, A. & Mason, S. G. 1967 The flow of suspensions through tubes. IV. Meniscus effects. J. Colloid Interface Sci. 23, 120–133.Google Scholar
Kim, J., Xu, F. & Lee, S. 2017 Formation and destabilization of the particle band on the fluid–fluid interface. Phys. Rev. Lett. 118, 074501.Google Scholar
van der Kooij, F. M., Kassapidou, K. & Lekkerkerker, H. N. W. 2000 Liquid crystal phase transitions in suspensions of polydisperse plate-like particles. Nature 406, 868–871.Google Scholar
Krishnan, G. & Leighton, D. T. 1994 Shear-induced size segregation phenomena in bidisperse suspensions. Appl. Mech. Rev. 47 (6), S236–S239.Google Scholar
Krishnan, G. P., Beimfohr, S. & Leighton, D. T. 1996 Shear-induced radial segregation in bidisperse suspensions. J. Fluid Mech. 321, 371–393.Google Scholar
Lecampion, B. & Garagash, D. I. 2014 Confined flow of suspensions modelled by a frictional rheology. J. Fluid Mech. 759, 197–235.Google Scholar
Lee, S., Stokes, Y. & Bertozzi, A. 2014 Behavior of a particle-laden flow in a spiral channel. Phys. Fluids 26, 043302.Google Scholar
Leighton, D. & Acrivos, A. 1987a Measurement of shear-induced self-diffusion in concentrated suspensions of spheres. J. Fluid Mech. 177, 109–131.Google Scholar
Leighton, D. & Acrivos, A. 1987b The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.Google Scholar
Lyon, M. K. & Leal, L. G. 1998a An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 1. Monodisperse systems. J. Fluid Mech. 363, 25–56.Google Scholar
Lyon, M. K. & Leal, L. G. 1998b An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 2. Bidisperse systems. J. Fluid Mech. 363, 57–77.Google Scholar
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stress. J. Rheol. 43, 1213–1237.Google Scholar
Morris, J. F. & Brady, J. F. 1998 Pressure-driven flow of a suspension: buoyancy effects. Intl J. Multiphase Flow 24, 105–130.Google Scholar
Murisic, N., Ho, J., Hu, V., Latterman, P., Koch, T., Lin, K., Mata, M. & Bertozzi, A. 2011 Particle-laden viscous thin-film flows on an incline: experiments compared with a theory based on shear-induced migration and particle settling. Physica D 240 (20), 1661–1673.Google Scholar
Murisic, N., Pausader, B., Peschka, D. & Bertozzi, A. L. 2013 Dynamics of particle settling and resuspension in viscous liquid films. J. Fluid Mech. 717, 203–231.Google Scholar
Norman, J. T., Oguntade, B. O. & Bonnecaze, R. T. 2008 Particle-phase distributions of pressure-driven flows of bidisperse suspensions. J. Fluid Mech. 594, 1–28.Google Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions – simulation and theory. J. Fluid Mech. 275, 157–199.Google Scholar
Ramachandran, A. & Leighton, D. T. 2007 The effect of gravity on the meniscus accumulation phenomenon in a tube. J. Rheol. 51 (5), 1073–1098.Google Scholar
Ramachandran, A. & Leighton, D. T. 2010 Particle migration in concentrated suspensions undergoing squeeze flow. J. Rheol. 54, 563–589.Google Scholar
Saffman, P. G. & Taylor, G. 1958 The penetration of a fluid into porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245, 312–329.Google Scholar
Shan, Y., Normand, M. & Peleg, M. 1997 Estimation of the surface concentration of adhered particles by colour imaging. Powder Technol. 92, 147–153.Google Scholar
Shapiro, A. P. & Probstein, R. F. 1992 Random packings of spheres and fluidity limits of monodisperse and bidisperse suspensions. Phys. Rev. Lett. 68, 1422–1425.Google Scholar
Shauly, A., Wachs, A. & Nir, A. 1998 Shear-induced particle migration in a polydisperse concentrated suspension. J. Rheol. 42, 1329–1348.Google Scholar
Snook, B., Butler, J. E. & Guazzelli, E. 2016 Dynamics of shear-induced migration of spherical particles in oscillatory pipe flow. J. Fluid Mech. 786, 128–153.Google Scholar
Storms, R. F., Ramarao, B. V. & Weiland, R. H. 1990 Low shear rate viscosity of bimodally dispersed suspensions. Powder Technol. 63, 247–259.Google Scholar
Tang, H., Grivas, W., Homentcovschi, D., Geer, J. & Singler, T. 2000 Stability considerations associated with the meniscoid particle band at advancing interfaces in Hele-Shaw suspension flow. Phys. Rev. Lett. 85, 2112–2115.Google Scholar
Xu, F., Kim, J. & Lee, S. 2016 Particle-induced viscous fingering. J. Non-Newtonian Fluid Mech. 238, 92–99.Google Scholar