Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T21:46:44.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Enhanced secondary motion of the turbulent flow through a porous square duct

Published online by Cambridge University Press:  06 November 2015

A. Samanta ,
R. Vinuesa ,
I. Lashgari ,
P. Schlatter  and
L. Brandt
A. Samanta*
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, 100 44 Stockholm, Sweden
R. Vinuesa
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, 100 44 Stockholm, Sweden
I. Lashgari
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, 100 44 Stockholm, Sweden
P. Schlatter
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, 100 44 Stockholm, Sweden
L. Brandt
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, 100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

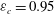Direct numerical simulations of the fully developed turbulent flow through a porous square duct are performed to study the effect of the permeable wall on the secondary cross-stream flow. The volume-averaged Navier–Stokes equations are used to describe the flow in the porous phase, a packed bed with porosity ${\it\varepsilon}_{c}=0.95$. The porous square duct is computed at 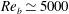$\mathit{Re}_{b}\simeq 5000$ and compared with the numerical simulations of a turbulent duct with four solid walls. The two boundary layers on the top wall and porous interface merge close to the centre of the duct, as opposed to the channel, because the sidewall boundary layers inhibit the growth of the shear layer over the porous interface. The most relevant feature in the porous duct is the enhanced magnitude of the secondary flow, which exceeds that of a regular duct by a factor of four. This is related to the increased vertical velocity, and the different interaction between the ejections from the sidewalls and the porous medium. We also report a significant decrease in the streamwise turbulence intensity over the porous wall of the duct (which is also observed in a porous channel), and the appearance of short spanwise rollers in the buffer layer, replacing the streaky structures of wall-bounded turbulence. These spanwise rollers most probably result from a Kelvin–Helmholtz type of instability, and their width is limited by the presence of the sidewalls.

JFM classification

Low-Reynolds-number flows: Porous media Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 681 - 693
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Breugem, W. P., Boersma, B.-J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562, 35–72.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 Nek5000: open source spectral element CFD solver. Available from: http://nek5000.mcs.anl.gov.Google Scholar
Gessner, F. B. 1973 The origin of secondary flow in turbulent flow along a corner. J. Fluid Mech. 58, 1–25.CrossRefGoogle Scholar
Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.CrossRefGoogle Scholar
Jiménez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.CrossRefGoogle Scholar
Noorani, A., El Khoury, G. K. & Schlatter, P. 2013 Evolution of turbulence characteristics from straight to curved pipes. Intl J. Heat Fluid Flow 41, 16–26.Google Scholar
Pinelli, A., Uhlmann, M., Sekimoto, A. & Kawahara, G. 2010 Reynolds number dependence of mean flow structure in square duct turbulence. J. Fluid Mech. 644, 107–122.Google Scholar
Prandtl, L. 1926 Über die ausgebildete Turbulenz. In Verh. 2nd Int. Kong. Tech. Mech. Zürich, pp. 62–75 (translation in NACA Tech. Memo. no. 435).Google Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.CrossRefGoogle Scholar
Vinuesa, R., Noorani, A., Lozano-Durán, A., El Khoury, G. K., Schlatter, P., Fischer, P. F. & Nagib, H. M. 2014 Aspect ratio effects in turbulent duct flows studied through direct numerical simulation. J. Turbul. 15, 677–706.Google Scholar
Vinuesa, R., Schlatter, P., Malm, J., Mavriplis, C. & Henningson, D. S. 2015a Direct numerical simulation of the flow around a wall-mounted square cylinder under various inflow conditions. J. Turbul. 16, 555–587.Google Scholar
Vinuesa, R., Schlatter, P. & Nagib, H. M. 2015b On minimum aspect ratio for duct flow facilities and the role of side walls in generating secondary flows. J. Turbul. 16, 588–606.Google Scholar
Whitaker, S. 1996 The Forchheimer equation: a theoretical development. Trans. Porous Med. 25, 27–61.Google Scholar
Zagni, A. F. M. & Smith, K. V. H. 1976 Stability of liquid flow down an inclined plane. J. Hydraul. Div. 102, 207–222.CrossRefGoogle Scholar
Zippe, H. J. & Graf, W. H. 1983 Turbulent boundary-layer flow over permeable and non-permeable rough surfaces. J. Hydraul. Res. 21, 51–65.Google Scholar