Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T12:49:06.522Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy production and self-sustained turbulence at the Kolmogorov scale in Couette flow

Published online by Cambridge University Press:  17 November 2017

Qiang Yang ,
Ashley P. Willis Open the ORCID record for Ashley P. Willis [Opens in a new window]  and
Yongyun Hwang Open the ORCID record for Yongyun Hwang [Opens in a new window]
Qiang Yang
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK School of Engineering and Centre for Scientific Computing, University of Warwick, Coventry CV4 7AL, UK
Ashley P. Willis
Affiliation:
School of Mathematics and Statistics, University of Sheffield, S3 7RH, UK
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Several recent studies have reported that there exists a self-similar form of invariant solutions down to the Kolmogorov microscale in the bulk region of turbulent Couette flow. While their role in a fully developed turbulent flow is yet to be identified, here we report that there exists a related mechanism of turbulence production at the Kolmogorov microscale in the bulk region of turbulent Couette flow by performing a set of minimal-span direct numerical simulations up to friction Reynolds number 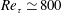$Re_{\unicode[STIX]{x1D70F}}\simeq 800$. This mechanism is found to essentially originate from the non-zero mean shear in the bulk region of the Couette flow, and involves eddy turn-over dynamics remarkably similar to the so-called self-sustaining process (SSP) and/or vortex–wave interaction (VWI). A numerical experiment that removes all other motions except in the core region is also performed, which demonstrates that the eddies at a given wall-normal location in the bulk region are sustained in the absence of other motions at different wall-normal locations. It is proposed that the self-sustaining eddies at the Kolmogorov microscale correspond to those in uniform shear turbulence at transitional Reynolds numbers, and a quantitative comparison between the eddies in uniform shear and near-wall turbulence is subsequently made. Finally, it is shown that turbulence production by the self-sustaining eddies at the Kolmogorov microscale is much smaller than that of full-scale simulations, and that the difference between the two increases with Reynolds number.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 834 , 10 January 2018 , pp. 531 - 554
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bewley, T. R. 2014 Numerical Renaissance: Simulation, Optimization, & Control. Renaissance Press.Google Scholar
Blackburn, H. M., Hall, P. & Sherwin, S. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flow. J. Fluid Mech. 726, R2.CrossRefGoogle Scholar
Chung, D., Chan, L., MacDonald, M., Hutchins, N. & Ooi, A. 2015 A fast direct numerical simulation method for characterising hydraulic roughness. J. Fluid Mech. 773, 418–431.CrossRefGoogle Scholar
Deguchi, K. 2015 Self-sustaining states at Kolmogorov microscale. J. Fluid Mech. 781, R6.CrossRefGoogle Scholar
Eckhardt, B. & Zammert, S. 2016 Exact coherent structures for the turbulent cascade. Bull. Am. Phys. Soc. 61 (20), A18.008.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.CrossRefGoogle Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.CrossRefGoogle Scholar
de Giovanetti, M., Hwang, Y. & Choi, H. 2016 Skin-friction generation by attached eddies in turbulent channel flow. J. Fluid Mech. 808, 511–538.CrossRefGoogle Scholar
Hall, P. & Sherwin, S. J. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.CrossRefGoogle Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex–wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.CrossRefGoogle Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Hwang, Y. 2016 Mesolayer of attached eddies in turbulent channel flow. Phys. Rev. Fluids 1 (6), 064401.CrossRefGoogle Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505.CrossRefGoogle ScholarPubMed
Hwang, Y., Willis, A. P. & Cossu, C. 2016 Invariant solutions of minimal large-scale structures in turbulent channel flow. J. Fluid Mech. 802, R1.CrossRefGoogle Scholar
Jeong, J., Benney, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.CrossRefGoogle Scholar
Jiménez, J., Kawahara, G., Simens, M. P., Nagata, M. & Shiba, M. 2005 Characterization of near-wall turbulence in terms of equilibrium and ‘bursting’ solutions. Phys. Fluids 17, 015105.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jiménez, J. & Simens, M. P. 2001 Low-dimensional dynamics of a turbulent wall flow. J. Fluid Mech. 435, 81–91.CrossRefGoogle Scholar
Jiménez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.CrossRefGoogle Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 209–303.Google Scholar
Kolmogorov, A. N. 1991 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. A 434, 9–13.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.CrossRefGoogle Scholar
Lee, M. K. & Moser, R. D. 2015 Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lumley, J. L. 1967 Similarity and the turbulent energy spectrum. Phys. Fluids 10, 855–858.CrossRefGoogle Scholar
MacDonald, M., Chung, D., Hutchins, N., Chan, L., Ooi, A. & Garcia-Mayoral, R. 2017 The minimal-span channel for rough-wall turbulent flows. J. Fluid Mech. 816, 5–42.CrossRefGoogle Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.CrossRefGoogle Scholar
Mizuno, Y. & Jiménez, J. 2013 Wall turbulence without walls. J. Fluid Mech. 723, 429–455.CrossRefGoogle Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Park, J. S. & Graham, M. D. 2016 Exact coherent states and connections to turbulent dynamics in minimal channel flow. J. Fluid Mech. 782, 430–454.CrossRefGoogle Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2014 Turbulence statistics in Couette flow at high Reynolds number. J. Fluid Mech. 758, 327–343.CrossRefGoogle Scholar
Rawat, S., Cossu, C., Hwang, Y. & Rincon, F. 2015 On the self-sustained nature of large-scale motions in turbulent Couette flow. J. Fluid Mech. 782, 515–540.CrossRefGoogle Scholar
Robertson, J. M. 1959 On turbulent plane Couette flow. In Proceedings of the Sixth Midwestern Conference on Fluid Mechanics, pp. 169–182. University of Texas, Austin.Google Scholar
Saddoughi, S. G. & Veeravallit, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Sekimoto, A., Dong, S. & Jiménez, J. 2016 Direct numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. Phys. Fluids 28, 035101.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1967 A First Course in Turbulence. MIT Press.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.CrossRefGoogle Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.CrossRefGoogle Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2016 Symmetry reduction in high dimensions, illustrated in a turbulent pipe. Phys. Rev. E 93, 022204.Google Scholar