Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T16:41:11.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy harvesting by flow-induced flutter in a simple model of an inverted piezoelectric flag

Published online by Cambridge University Press:  10 February 2016

Kourosh Shoele  and
Rajat Mittal
Kourosh Shoele
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Rajat Mittal*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Two-dimensional numerical simulations are used to study the coupled fluid–structure–electric interaction of a simple model of an inverted piezoelectric flag, and to investigate the dynamics of the flow–structure interaction of this configuration as well as its energy harvesting performance. In particular, the dynamic response of the inverted flag as well as the associated flow patterns are examined for a range of inertia, bending stiffness and Reynolds numbers, and categorized into distinct vibrational states based on the symmetry of the motion as well as the amplitude. Simulations indicate that large-amplitude vibrations can be achieved over a large range of parameters and there is also evidence of lock-on between the flag flutter and the intrinsic wake shedding phenomenon. 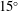The initial inclination of the flag to the prevailing flow is found to significantly affect the flutter performance for inclination angles exceeding $15^{\circ }$. The state with large symmetric flutter is identified as being most promising for energy harvesting, and the effect of piezoelectric material parameters on the energy harvesting performance of this flutter state is examined in detail. The maximum energy efficiency of the flags is found to be approximately 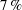$7\,\%$, and the maximum occurs when there is a match between the time scales of flutter and the intrinsic time scale of the piezoelectric circuit. The simulations are used to examine a simple scaling law that could be used to predict the energy harvesting performance of such devices.

JFM classification

Mathematical Foundations: Computational methods Mathematical Foundations: General fluid mechanics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , pp. 582 - 606
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akaydin, H. D., Elvin, N. & Andreopoulos, Y. 2010 Energy harvesting from highly unsteady fluid flows using piezoelectric materials. J. Intell. Mater. Syst. Struct. 21 (13), 1263–1278.CrossRefGoogle Scholar
Akcabay, D. T. & Young, Y. L. 2012a Hydroelastic response and energy harvesting potential of flexible piezoelectric beams in viscous flow. Phys. Fluids 24 (5), 054106.CrossRefGoogle Scholar
Akcabay, D. T. & Young, Y. L. 2012b Scaling the dynamic response and energy harvesting potential of piezoelectric beams. Appl. Phys. Lett. 101 (26), 264104.Google Scholar
Alben, S. & Shelley, M. J. 2008 Flapping states of a flag in an inviscid fluid: bistability and the transition to chaos. Phys. Rev. Lett. 100 (7), 074301.CrossRefGoogle Scholar
Anton, S. R. & Sodano, H. A. 2007 A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 16 (3), R1.CrossRefGoogle Scholar
Audoly, B. & Pomeau, Y. 2010 Elasticity and Geometry. Oxford University Press.Google Scholar
Bhardwaj, R. & Mittal, R. 2012 Benchmarking a coupled immersed-boundary-finite-element solver for large-scale flow-induced deformation. AIAA J. 50 (7), 1638–1642.CrossRefGoogle Scholar
Blevins, R. D. 1977 Flow-Induced Vibration. Van Nostrand Reinhold.Google Scholar
Cha, Y., Kim, H. & Porfiri, M. 2013 Energy harvesting from underwater base excitation of a piezoelectric composite beam. Smart Mater. Struct. 22 (11), 115026.CrossRefGoogle Scholar
Connell, B. S. H & Yue, D. K. P. 2007 Flapping dynamics of a flag in a uniform stream. J. Fluid Mech. 581, 33–67.CrossRefGoogle Scholar
Doare, O. & Michelin, S. 2011 Piezoelectric coupling in energy-harvesting fluttering flexible plates: linear stability analysis and conversion efficiency. J. Fluids Struct. 27 (8), 1357–1375.CrossRefGoogle Scholar
Dong, H., Bozkurttas, M., Mittal, R., Madden, P. & Lauder, G. V. 2010 Computational modelling and analysis of the hydrodynamics of a highly deformable fish pectoral fin. J. Fluid Mech. 645, 345–373.CrossRefGoogle Scholar
Eloy, C., Souilliez, C. & Schouveiler, L. 2007 Flutter of a rectangular plate. J. Fluids Struct. 23 (6), 904–919.CrossRefGoogle Scholar
Goldstein, D., Handler, R. & Sirovich, L. 1993 Modeling a no-slip flow boundary with an external force field. J. Comput. Phys. 105 (2), 354–366.CrossRefGoogle Scholar
Guo, C. Q. & Paidoussis, M. P. 2000 Analysis of hydroelastic instabilities of rectangular parallel-plate assemblies. Trans. ASME J. Press. Vessel Technol. 122 (4), 502–508.CrossRefGoogle Scholar
Huang, L. 1995 Flutter of cantilevered plates in axial flow. J. Fluids Struct. 9 (2), 127–147.CrossRefGoogle Scholar
Huang, W.-X., Shin, S. J. & Sung, H. J. 2007 Simulation of flexible filaments in a uniform flow by the immersed boundary method. J. Comput. Phys. 226 (2), 2206–2228.CrossRefGoogle Scholar
Huang, W.-X. & Sung, H. J. 2009 An immersed boundary method for fluid–flexible structure interaction. Comput. Meth. Appl. Mech. Engng 198 (33), 2650–2661.CrossRefGoogle Scholar
Kim, D., Cossé, J., Cerdeira, C. H. & Gharib, M. 2013 Flapping dynamics of an inverted flag. J. Fluid Mech. 736, R1.CrossRefGoogle Scholar
Kim, G. & Davis, D. C. 1995 Hydrodynamic instabilities in flat-plate-type fuel assemblies. Nucl. Engng Design 158 (1), 1–17.CrossRefGoogle Scholar
Kim, H. S., Kim, J.-H. & Kim, J. 2011 A review of piezoelectric energy harvesting based on vibration. Intl J. Precis. Engng Manuf. 12 (6), 1129–1141.CrossRefGoogle Scholar
Kim, K., Baek, S. J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.CrossRefGoogle Scholar
Koochesfahani, M. M. 1989 Vortical patterns in the wake of an oscillating airfoil. AIAA J. 27 (9), 1200–1205.CrossRefGoogle Scholar
Kornecki, A., Dowell, E. H. & O’Brien, J. 1976 On the aeroelastic instability of two-dimensional panels in uniform incompressible flow. J. Sound Vib. 47 (2), 163–178.CrossRefGoogle Scholar
Lighthill, J. 1975 Mathematica Biofluiddynamics. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Michelin, S. & Doare, O. 2013 Energy harvesting efficiency of piezoelectric flags in axial flows. J. Fluid Mech. 714, 489–504.CrossRefGoogle Scholar
Michelin, S. & Smith, S. G. L. 2009 Resonance and propulsion performance of a heaving flexible wing. Phys. Fluids 21 (7), 071902.CrossRefGoogle Scholar
Miller, D. R. 1960 Critical flow velocities for collapse of reactor parallel-plate fuel assemblies. J. Engng Power 82 (2), 83–91.CrossRefGoogle Scholar
Paidoussis, M. P., Price, S. J. & De Langre, E. 2010 Fluid–Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.CrossRefGoogle Scholar
Peskin, C. S. 1972 Flow patterns around heart valves: a numerical method. J. Comput. Phys. 10 (2), 252–271.CrossRefGoogle Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.CrossRefGoogle Scholar
Ryu, J., Park, S. G., Kim, B. & Sung, H. J. 2015 Flapping dynamics of an inverted flag in a uniform flow. J. Fluids Struct. 57, 159–169.CrossRefGoogle Scholar
Saad, Y.1990 SPARSKIT: A basic toolkit for sparse matrix computations. Research Institute for Advanced Computer Science, NASA Ames Research Center, Moffet Field, CA.Google Scholar
Shelley, M., Vandenberghe, N. & Zhang, J. 2005 Heavy flags undergo spontaneous oscillations in flowing water. Phys. Rev. Lett. 94 (9), 094302.CrossRefGoogle ScholarPubMed
Shelley, M. J. & Zhang, J. 2011 Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 43, 449–465.CrossRefGoogle Scholar
Shoele, K. & Mittal, R. 2014 Computational study of flow-induced vibration of a reed in a channel and effect on convective heat transfer. Phys. Fluids 26 (12), 127103.CrossRefGoogle Scholar
Shoele, K. & Zhu, Q. 2010 Flow-induced vibrations of a deformable ring. J. Fluid Mech. 650, 343–362.CrossRefGoogle Scholar
Shoele, K. & Zhu, Q. 2012 Leading edge strengthening and the propulsion performance of flexible ray fins. J. Fluid Mech. 693, 402–432.CrossRefGoogle Scholar
Shoele, K. & Zhu, Q. 2013 Performance of a wing with nonuniform flexibility in hovering flight. Phys. Fluids 25, 041901.CrossRefGoogle Scholar
Shoele, K. & Zhu, Q. 2015 Performance of synchronized fins in biomimetic propulsion. Bioinspir. Biomim. 10 (2), 026008.CrossRefGoogle ScholarPubMed
Sodano, H. A., Inman, D. J. & Park, G. 2004 A review of power harvesting from vibration using piezoelectric materials. Shock Vib. Dig. 36 (3), 197–206.CrossRefGoogle Scholar
Stanton, S. C., Erturk, A., Mann, B. P., Dowell, E. H. & Inman, D. J. 2012 Nonlinear nonconservative behavior and modeling of piezoelectric energy harvesters including proof mass effects. J. Intell. Mater. Syst. Struct. 23 (2), 183–199.CrossRefGoogle Scholar
Tang, C., Liu, N.-S. & Lu, X.-Y. 2015 Dynamics of an inverted flexible plate in a uniform flow. Phys. Fluids 27 (7), 073601.CrossRefGoogle Scholar
Tang, L., Paidoussis, M. P. & Jiang, J. 2009 Cantilevered flexible plates in axial flow: energy transfer and the concept of flutter-mill. J. Sound Vib. 326 (1), 263–276.CrossRefGoogle Scholar
Tang, D. M., Yamamoto, H. & Dowell, E. H. 2003 Flutter and limit cycle oscillations of two-dimensional panels in three-dimensional axial flow. J. Fluids Struct. 17 (2), 225–242.CrossRefGoogle Scholar
Tetlow, G. A. & Lucey, A. D. 2009 Motions of a cantilevered flexible plate in viscous channel flow driven by a constant pressure drop. Commun. Numer. Meth. Engng 25 (5), 463–482.CrossRefGoogle Scholar
Theodorsen, T. & Mutchler, W. H.1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. 496.Google Scholar
Tornberg, A.-K. & Shelley, M. J. 2004 Simulating the dynamics and interactions of flexible fibers in Stokes flows. J. Comput. Phys. 196 (1), 8–40.CrossRefGoogle Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Gopalkrishnan, R. 1991 Wake mechanics for thrust generation in oscillating foils. Phys. Fluids A 3 (12), 2835–2837.CrossRefGoogle Scholar
Turek, S. & Hron, J. 2006 Proposal for Numerical Benchmarking of Fluid–Structure Interaction Between an Elastic Object and Laminar Incompressible Flow. Springer.CrossRefGoogle Scholar
Wang, D.-A. & Ko, H.-H. 2010 Piezoelectric energy harvesting from flow-induced vibration. J. Micromech. Microengng 20 (2), 025019.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Yang, Y., Zhao, L. & Tang, L. 2013 Comparative study of tip cross-sections for efficient galloping energy harvesting. Appl. Phys. Lett. 102 (6), 064105.Google Scholar
Zhang, J., Childress, S., Libchaber, A. & Shelley, M. 2000 Flexible filaments in a flowing soap film as a model for one-dimensional flags in a two-dimensional wind. Nature 408 (6814), 835–839.CrossRefGoogle Scholar
Zhao, L., Tang, L. & Yang, Y. 2013 Comparison of modeling methods and parametric study for a piezoelectric wind energy harvester. Smart Mater. Struct. 22 (12), 125003.CrossRefGoogle Scholar
Zhu, Q., Wolfgang, M. J., Yue, D. K. P. & Triantafyllou, M. S. 2002 Three-dimensional flow structures and vorticity control in fish-like swimming. J. Fluid Mech. 468, 1–28.CrossRefGoogle Scholar