Article contents
Energy fluxes in quasi-equilibrium flows
Published online by Cambridge University Press: 17 December 2019
Abstract
We examine the relation between the absolute equilibrium state of the spectrally truncated Euler equations (TEE) predicted by Kraichnan (J. Fluid Mech., vol. 59 (4), 1973, pp. 745–752) to the forced and dissipated flows of the spectrally truncated Navier–Stokes (TNS) equations. In both of these idealized systems, a finite number of Fourier modes is kept contained inside a sphere of radius  $k_{max}$, but, while the first conserves energy, in the second, energy is injected by a body-force
$k_{max}$, but, while the first conserves energy, in the second, energy is injected by a body-force  $\boldsymbol{f}$ and dissipated by the viscosity
$\boldsymbol{f}$ and dissipated by the viscosity  $\unicode[STIX]{x1D708}$. For the TNS system, stochastically forced with energy injection rate
$\unicode[STIX]{x1D708}$. For the TNS system, stochastically forced with energy injection rate  ${\mathcal{I}}_{{\mathcal{E}}}$, we show, using an asymptotic expansion of the Fokker-Planck equation, that in the limit of small
${\mathcal{I}}_{{\mathcal{E}}}$, we show, using an asymptotic expansion of the Fokker-Planck equation, that in the limit of small  $k_{max}\unicode[STIX]{x1D702}$ (where
$k_{max}\unicode[STIX]{x1D702}$ (where  $\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/{\mathcal{I}}_{{\mathcal{E}}})^{1/4}$, the Kolmogorov length scale) the flow approaches the absolute equilibrium solution of Kraichnan with an effective ‘temperature’ such that there is a balance between the energy injection and the energy dissipation rate. We further investigate the TNS system using direct numerical simulations in periodic cubic boxes of size
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/{\mathcal{I}}_{{\mathcal{E}}})^{1/4}$, the Kolmogorov length scale) the flow approaches the absolute equilibrium solution of Kraichnan with an effective ‘temperature’ such that there is a balance between the energy injection and the energy dissipation rate. We further investigate the TNS system using direct numerical simulations in periodic cubic boxes of size  $2\unicode[STIX]{x03C0}/k_{0}$. The simulations verify the predictions of the model for small values of
$2\unicode[STIX]{x03C0}/k_{0}$. The simulations verify the predictions of the model for small values of  $k_{max}\unicode[STIX]{x1D702}$. For intermediate values of
$k_{max}\unicode[STIX]{x1D702}$. For intermediate values of  $k_{max}\unicode[STIX]{x1D702}$, a transition from the quasi-equilibrium ‘thermal’ state to Kolmogorov turbulence is observed. In particular, we demonstrate that, at steady state, the TNS system reproduces the Kolmogorov energy spectrum if
$k_{max}\unicode[STIX]{x1D702}$, a transition from the quasi-equilibrium ‘thermal’ state to Kolmogorov turbulence is observed. In particular, we demonstrate that, at steady state, the TNS system reproduces the Kolmogorov energy spectrum if  $k_{max}\unicode[STIX]{x1D702}\gg 1$. As
$k_{max}\unicode[STIX]{x1D702}\gg 1$. As  $k_{max}\unicode[STIX]{x1D702}$ becomes smaller, then a bottleneck effect appears, taking the form of the equipartition spectrum
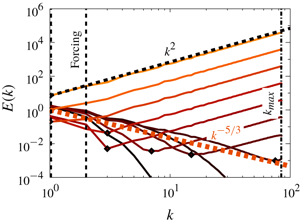
$k_{max}\unicode[STIX]{x1D702}$ becomes smaller, then a bottleneck effect appears, taking the form of the equipartition spectrum  $E(k)\propto k^{2}$ at small scales. As
$E(k)\propto k^{2}$ at small scales. As  $k_{max}\unicode[STIX]{x1D702}$ is decreased even further, so that
$k_{max}\unicode[STIX]{x1D702}$ is decreased even further, so that  $k_{max}\unicode[STIX]{x1D702}\ll (k_{0}/k_{max})^{11/4}$, the equipartition spectrum occupies all scales approaching the asymptotic equilibrium solutions found before. If the forcing is applied at small scales and the dissipation acts only at large scales, then the equipartition spectrum appears at all scales for all values of
$k_{max}\unicode[STIX]{x1D702}\ll (k_{0}/k_{max})^{11/4}$, the equipartition spectrum occupies all scales approaching the asymptotic equilibrium solutions found before. If the forcing is applied at small scales and the dissipation acts only at large scales, then the equipartition spectrum appears at all scales for all values of  $\unicode[STIX]{x1D708}$. In both cases, a finite forward or inverse flux is present even for the cases where the flow is close to the equilibrium state solutions. However, unlike the classical turbulence, where an energy cascade develops with a mean energy flux that is large compared to its fluctuations, the quasi-equilibrium state has a mean flux of energy that is subdominant to the large flux fluctuations observed.
$\unicode[STIX]{x1D708}$. In both cases, a finite forward or inverse flux is present even for the cases where the flow is close to the equilibrium state solutions. However, unlike the classical turbulence, where an energy cascade develops with a mean energy flux that is large compared to its fluctuations, the quasi-equilibrium state has a mean flux of energy that is subdominant to the large flux fluctuations observed.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 14
- Cited by


