Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T12:41:09.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Emergence of superwalking droplets

Published online by Cambridge University Press:  09 November 2020

Rahil N. Valani Open the ORCID record for Rahil N. Valani [Opens in a new window] ,
Jack Dring ,
Tapio P. Simula Open the ORCID record for Tapio P. Simula [Opens in a new window]  and
Anja C. Slim
Rahil N. Valani*
Affiliation:
School of Physics and Astronomy, Monash University, Victoria3800, Australia
Jack Dring
Affiliation:
School of Mathematics, Monash University, Victoria3800, Australia
Tapio P. Simula
Affiliation:
Optical Sciences Centre, Swinburne University of Technology, Melbourne3122, Australia
Anja C. Slim
Affiliation:
School of Mathematics, Monash University, Victoria3800, Australia School of Earth, Atmosphere and Environment, Monash University, Victoria3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

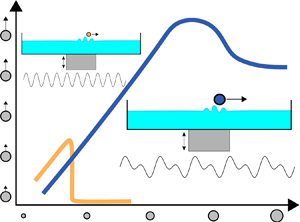
A new class of self-propelled droplets, coined superwalkers, has been shown to emerge when a bath of silicone oil is vibrated simultaneously at a given frequency and its subharmonic tone with a relative phase difference between them (Valani et al., Phys. Rev. Lett., vol. 123, 2019, 024503). To understand the emergence of superwalking droplets, we explore their vertical and horizontal dynamics by extending previously established theoretical models for walkers driven by a single frequency to superwalkers driven by two frequencies. Here, we show that driving the bath at two frequencies with an appropriate phase difference raises every second peak and lowers the intermediate peaks in the vertical periodic motion of the fluid surface. This allows large droplets that could otherwise not walk to leap over the intermediate peaks, resulting in superwalking droplets whose vertical dynamics is qualitatively similar to normal walkers. We find that the droplet's vertical and horizontal dynamics are strongly influenced by the relative height difference between successive peaks of the bath motion, a parameter that is controlled by the phase difference. Comparison of our simulated superwalkers with the experiments of Valani et al. (2019) shows good agreement for small- to moderate-sized superwalkers.

JFM classification

Drops and Bubbles: Drops Waves/Free-surface Flows: Capillary waves Waves/Free-surface Flows: Faraday waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 906 , 10 January 2021 , A3
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arbelaiz, J., Oza, A. U. & Bush, J. W. M. 2018 Promenading pairs of walking droplets: dynamics and stability. Phys. Rev. Fluids 3, 013604.CrossRefGoogle Scholar
Besson, T., Edwards, W. S. & Tuckerman, L. S. 1996 Two-frequency parametric excitation of surface waves. Phys. Rev. E 54, 507–513.CrossRefGoogle ScholarPubMed
Blanchette, F. 2016 Modeling the vertical motion of drops bouncing on a bounded fluid reservoir. Phys. Fluids 28 (3), 032104.10.1063/1.4942446CrossRefGoogle Scholar
Bush, J. W. M. 2015 Pilot-wave hydrodynamics. Annu. Rev. Fluid Mech. 47, 269–292.CrossRefGoogle Scholar
Bush, J. W. M., Couder, Y., Gilet, T., Milewski, P. A. & Nachbin, A. 2018 Introduction to focus issue on hydrodynamic quantum analogs. Chaos 28 (9), 096001.CrossRefGoogle ScholarPubMed
Couchman, M. M. P., Turton, S. E. & Bush, J. W. M. 2019 Bouncing phase variations in pilot-wave hydrodynamics and the stability of droplet pairs. J. Fluid Mech. 871, 212–243.CrossRefGoogle Scholar
Couder, Y., Fort, E., Gautier, C.-H. & Boudaoud, A. 2005 a From bouncing to floating: noncoalescence of drops on a fluid bath. Phys. Rev. Lett. 94 (17), 177801.CrossRefGoogle ScholarPubMed
Couder, Y., Protiere, S., Fort, E. & Boudaoud, A. 2005 b Dynamical phenomena: walking and orbiting droplets. Nature 437 (7056), 208–208.CrossRefGoogle ScholarPubMed
Cristea-Platon, T., Sáenz, P. J. & Bush, J. W. M. 2018 Walking droplets in a circular corral: quantisation and chaos. Chaos 28 (9), 096116.CrossRefGoogle Scholar
Durey, M. & Milewski, P. A. 2017 Faraday wave–droplet dynamics: discrete-time analysis. J. Fluid Mech. 821, 296–329.CrossRefGoogle Scholar
Durey, M., Milewski, P. A. & Wang, Z. 2020 Faraday pilot-wave dynamics in a circular corral. J. Fluid Mech. 891, A3.CrossRefGoogle Scholar
Eddi, A., Fort, E., Moisy, F. & Couder, Y. 2009 Unpredictable tunneling of a classical wave-particle association. Phys. Rev. Lett. 102 (24), 240401.10.1103/PhysRevLett.102.240401CrossRefGoogle ScholarPubMed
Eddi, A., Moukhtar, J., Perrard, S., Fort, E. & Couder, Y. 2012 Level splitting at macroscopic scale. Phys. Rev. Lett. 108, 264503.CrossRefGoogle ScholarPubMed
Eddi, A., Sultan, E., Moukhtar, J., Fort, E., Rossi, M. & Couder, Y. 2011 Information stored in Faraday waves: the origin of a path memory. J. Fluid Mech. 674, 433–463.CrossRefGoogle Scholar
Faraday, M. 1831 On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Phil. Trans. R. Soc. Lond. I 121, 299–340.Google Scholar
Fort, E., Eddi, A., Boudaoud, A., Moukhtar, J. & Couder, Y. 2010 Path-memory induced quantization of classical orbits. Proc. Natl Acad. Sci. USA 107 (41), 17515–17520.CrossRefGoogle Scholar
Galeano-Rios, C. A., Milewski, P. A. & Vanden-Broeck, J. -M. 2017 Non-wetting impact of a sphere onto a bath and its application to bouncing droplets. J. Fluid Mech. 826, 97–127.CrossRefGoogle Scholar
Galeano-Rios, C. A., Milewski, P. A. & Vanden-Broeck, J. -M. 2019 Quasi-normal free-surface impacts, capillary rebounds and application to Faraday walkers. J. Fluid Mech. 873, 856–888.CrossRefGoogle Scholar
Gilet, T. 2016 Quantumlike statistics of deterministic wave-particle interactions in a circular cavity. Phys. Rev. E 93, 042202.CrossRefGoogle Scholar
Gilet, T. & Bush, J. W. M. 2009 a Chaotic bouncing of a droplet on a soap film. Phys. Rev. Lett. 102, 014501.CrossRefGoogle ScholarPubMed
Gilet, T. & Bush, J. W. M. 2009 b The fluid trampoline: droplets bouncing on a soap film. J. Fluid Mech. 625, 167–203.CrossRefGoogle Scholar
Gilet, T., Terwagne, D., Vandewalle, N. & Dorbolo, S. 2008 Dynamics of a bouncing droplet onto a vertically vibrated interface. Phys. Rev. Lett. 100, 167802.CrossRefGoogle ScholarPubMed
Harris, D. M. & Bush, J. W. M. 2014 Droplets walking in a rotating frame: from quantized orbits to multimodal statistics. J. Fluid Mech. 739, 444–464.CrossRefGoogle Scholar
Harris, D. M., Moukhtar, J., Fort, E., Couder, Y. & Bush, J. W. M. 2013 Wavelike statistics from pilot-wave dynamics in a circular corral. Phys. Rev. E 88, 011001.CrossRefGoogle Scholar
Kumar, K. 1996 Linear theory of faraday instability in viscous liquids. Proc. R. Soc. Lond. A 452 (1948), 1113–1126.Google Scholar
Kumar, K. & Tuckerman, L. S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.CrossRefGoogle Scholar
Labousse, M., Oza, A. U., Perrard, S. & Bush, J. W. M. 2016 Pilot-wave dynamics in a harmonic potential: quantization and stability of circular orbits. Phys. Rev. E 93, 033122.CrossRefGoogle Scholar
Milewski, P. A., Galeano-Rios, C. A., Nachbin, A. & Bush, J. W. M. 2015 Faraday pilot-wave dynamics: modelling and computation. J. Fluid Mech. 778, 361–388.CrossRefGoogle Scholar
Moláček, J. & Bush, J. W. M. 2013 a Drops bouncing on a vibrating bath. J. Fluid Mech. 727, 582–611.CrossRefGoogle Scholar
Moláček, J. & Bush, J. W. M. 2013 b Drops walking on a vibrating bath: towards a hydrodynamic pilot-wave theory. J. Fluid Mech. 727, 612–647.CrossRefGoogle Scholar
Müller, H. W. 1993 Periodic triangular patterns in the Faraday experiment. Phys. Rev. Lett. 71, 3287–3290.CrossRefGoogle ScholarPubMed
Nachbin, A. 2018 Walking droplets correlated at a distance. Chaos 28 (9), 096110.CrossRefGoogle ScholarPubMed
Nachbin, A., Milewski, P. A. & Bush, J. W. M. 2017 Tunneling with a hydrodynamic pilot-wave model. Phys. Rev. Fluids 2, 034801.CrossRefGoogle Scholar
Oza, A. U., Harris, D. M., Rosales, R. R. & Bush, J. W. M. 2014 Pilot-wave dynamics in a rotating frame: on the emergence of orbital quantization. J. Fluid Mech. 744, 404–429.CrossRefGoogle Scholar
Oza, A. U., Rosales, R. R. & Bush, J. W. M. 2013 A trajectory equation for walking droplets: hydrodynamic pilot-wave theory. J. Fluid Mech. 737, 552–570.CrossRefGoogle Scholar
Oza, A. U., Rosales, R. R. & Bush, J. W. M. 2018 Hydrodynamic spin states. Chaos 28 (9), 096106.CrossRefGoogle ScholarPubMed
Oza, A. U., Siéfert, E., Harris, D. M., Moláček, J. & Bush, J. W. M. 2017 Orbiting pairs of walking droplets: dynamics and stability. Phys. Rev. Fluids 2 (5), 053601.CrossRefGoogle Scholar
Perrard, S., Labousse, M., Fort, E. & Couder, Y. 2014 a Chaos driven by interfering memory. Phys. Rev. Lett. 113, 104101.CrossRefGoogle ScholarPubMed
Perrard, S., Labousse, M., Miskin, M., Fort, E. & Couder, Y. 2014 b Self-organization into quantized eigenstates of a classical wave-driven particle. Nat. Commun. 5, 3219.CrossRefGoogle ScholarPubMed
Protière, S., Boudaoud, A. & Couder, Y. 2006 Particle–wave association on a fluid interface. J. Fluid Mech. 554, 85–108.CrossRefGoogle Scholar
Sáenz, P. J., Cristea-Platon, T. & Bush, J. W. M. 2018 Statistical projection effects in a hydrodynamic pilot-wave system. Nat. Phys. 14 (3), 315–319.CrossRefGoogle Scholar
Sáenz, P. J., Cristea-Platon, T. & Bush, J. W. M. 2020 A hydrodynamic analog of Friedel oscillations. Sci. Adv. 6 (20).CrossRefGoogle ScholarPubMed
Sampara, N. & Gilet, T. 2016 Two-frequency forcing of droplet rebounds on a liquid bath. Phys. Rev. E 94, 053112.CrossRefGoogle ScholarPubMed
Sprott, J. C. 2003 Chaos and Time-Series Analysis. Oxford University Press.Google Scholar
Tadrist, L., Gilet, T., Schlagheck, P. & Bush, J. W. M. 2020 Predictability in a hydrodynamic pilot-wave system: resolution of walker tunneling. Phys. Rev. E 102, 013104.CrossRefGoogle Scholar
Tadrist, L., Shim, J.-B., Gilet, T. & Schlagheck, P. 2018 Faraday instability and subthreshold Faraday waves: surface waves emitted by walkers. J. Fluid Mech. 848, 906–945.CrossRefGoogle Scholar
Thomas, G. B. & Finney, R. L. 1996 Calculus and Analytic Geometry, 9th edn. Addison-Wesley.Google Scholar
Turton, S. E., Couchman, M. M. P. & Bush, J. W. M. 2018 A review of the theoretical modeling of walking droplets: toward a generalized pilot-wave framework. Chaos 28 (9), 096111.CrossRefGoogle Scholar
Valani, R. N., Slim, A. C. & Simula, T. 2018 Hong–Ou–Mandel-like two-droplet correlations. Chaos 28 (9), 096104.CrossRefGoogle ScholarPubMed
Valani, R. N., Slim, A. C. & Simula, T. 2019 Superwalking droplets. Phys. Rev. Lett. 123, 024503.CrossRefGoogle ScholarPubMed
Walker, J. 1978 Drops of liquids can be made to float on the liquid. What enables them to do so? Sci. Am. 238 (6), 123–129.Google Scholar
Wind-Willassen, Ø., Moláček, J., Harris, D. M. & Bush, J. W. M. 2013 Exotic states of bouncing and walking droplets. Phys. Fluids 25 (8), 082002.CrossRefGoogle Scholar