Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T18:01:32.490Z Has data issue: false hasContentIssue false
  • English
  • Français

The emergence of localized vortex–wave interaction states in plane Couette flow

Published online by Cambridge University Press:  13 March 2013

Kengo Deguchi ,
Philip Hall  and
Andrew Walton
Kengo Deguchi
Affiliation:
Department of Aeronautics and Astronautics, Graduate School of Engineering, Kyoto University, Kyoto 606-8501, Japan
Philip Hall*
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
Andrew Walton
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The recently understood relationship between high-Reynolds-number vortex–wave interaction theory and computationally generated self-sustaining processes provides a possible route to an understanding of some of the underlying structures of fully turbulent flows. Here vortex–wave interaction (VWI) theory is used in the long streamwise wavelength limit to continue the development found at order-one wavelengths by Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). The asymptotic description given reduces the Navier–Stokes equations to the so-called boundary-region equations, for which we find equilibrium states describing the change in the VWI as the wavelength of the wave increases from 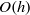$O(h)$ to 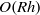$O(Rh)$, where 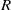$R$ is the Reynolds number and 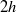$2h$ is the depth of the channel. The reduced equations do not include the streamwise pressure gradient of the perturbation or the effect of streamwise diffusion of the wave–vortex states. The solutions we calculate have an asymptotic error proportional to 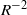${R}^{- 2} $ when compared to the full Navier–Stokes equations. The results found correspond to the minimum drag configuration for VWI states and might therefore be of relevance to the control of turbulent flows. The key feature of the new states discussed here is the thickening of the critical layer structure associated with the wave part of the flow to completely fill the channel, so that the roll part of the flow is driven throughout the flow rather than as in Hall & Sherwin as a stress discontinuity across the critical layer. We identify a critical streamwise wavenumber scaling, which, when approached, causes the flow to localize and take on similarities with computationally generated or experimentally observed turbulent spots. In effect, the identification of this critical wavenumber for a given value of the assumed high Reynolds number fixes a minimum box length necessary for the emergence of localized structures. Whereas nonlinear equilibrium states of the Navier–Stokes equations are thought to form a backbone on which turbulent flows hang, our results suggest that the localized states found here might play a related role for turbulent spots.

JFM classification

Instability: Nonlinear instability Turbulent Flows: Shear layer turbulence Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 58 - 85
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benney, D. 1984 The evolution of disturbances in shear flows at high Reynolds numbers. Stud. Appl. Maths 70, 1–19.Google Scholar
Chen, C. S. & Kuo, W. J. 2004 Heat transfer characteristics of gaseous flow in long mini- and microtubes. Numer. Heat Transfer A 46, 497–514.Google Scholar
Clever, R. M. & Busse, F. H. 1997 Tertiary and quaternary solutions for plane Couette flow. J. Fluid Mech. 344, 137–153.CrossRefGoogle Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2009 Localized edge states in plane Couette flow. Phys. Fluids 21, 111701.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Fletcher, C. A. J. 1991 Computational Techniques for Fluid Dynamics, 2. Springer.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 1–24.CrossRefGoogle Scholar
Gittler, P. 1993 Stability of axial Poiseuille–Couette flow between concentric cylinders. Acta Mech. 101, 1–13.Google Scholar
Goldstein, M. E. & Wundrow, D. W. 1998 On the environmental realizability of algebraically growing disturbances and their relation to Klebanoff modes. Theor. Comput. Fluid Dyn. 10, 171–186.Google Scholar
Goldstein, M. E. & Sescu, A. 2008 Boundary-layer transition at high free stream disturbance levels – beyond Klebanoff modes. J. Fluid Mech. 613, 95–124.CrossRefGoogle Scholar
Hall, P. 1988 The nonlinear development of Görtler vortices in growing boundary layers. J. Fluid Mech. 193, 243–266.Google Scholar
Hall, P. 2012a Vortex–wave interactions/self-sustained processes in high Prandtl number natural convection in a vertical channel with moving sidewalls. Stud. Appl. Maths 129, 1–25.Google Scholar
Hall, P. 2012b Vortex–wave interactions: long-wavelength streaks and spatial localization in natural convection. J. Fluid Mech. 703, 99–110.Google Scholar
Hall, P. & Horseman, N. J. 1991 The linear inviscid secondary instability of longitudinal vortex structures in boundary layers. J. Fluid Mech. 232, 357–375.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1989 Nonlinear Tollmien–Schlichting/vortex interaction in boundary layers. Eur. J. Mech. (B/Fluids) 8 (3), 179–205.Google Scholar
Hall, P. & Smith, F. T. 1990 Near Planar TS Waves and Longitudinal Vortices in Channel Flow: Nonlinear Interaction and Focussing, pp. 5–39 Springer.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Higuera, M. & Vega, J. 2009 Modal description of internal optimal streaks. J. Fluid Mech. 626, 21–31.Google Scholar
Itano, T. & Generalis, S. C. 2009 Hairpin vortex solution in planar Couette flow: a tapestry of knotted vortices. Phys. Rev. Lett 102, 114501.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.Google Scholar
Joseph, D. D. & Carmi, S. 1969 Stability of Poiseuille flow in pipes, annuli, and channels. Q. Appl. Maths 26, 575–599.Google Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.CrossRefGoogle Scholar
Kerswell, R. R & Tutty, O. R. 2007 Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
Komminaho, K., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.Google Scholar
Luchini, P. 2000 Reynolds-number-independent instability of the boundary layer over a flat surface: optimal perturbations. J. Fluid Mech. 404, 289–309.Google Scholar
Lundbladh, A. & Johansson, A. V. 1991 Direct simulation of turbulent spots in plane Couette flow. J. Fluid Mech. 229, 499–516.CrossRefGoogle Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Peris, R., Marquina, A. & Candela, V. 2011 The convergence of the perturbed Newton method and its application for ill-conditioned problems. Appl. Maths Comput. 218, 2988–3001.Google Scholar
Schneider, T. M., Marinc, D. & Eckhardt, B 2010a Localized edge states nucleate turbulence in extended plane Couette cells. J. Fluid Mech. 646, 441–451.Google Scholar
Schneider, T. M., Gibson, J. F. & Burke, J. 2010b Snakes and ladders: localized solutions of plane Couette flow. Phys. Rev. Lett. 104, 104501.CrossRefGoogle ScholarPubMed
Schneider, T. M., Gibson, J. F., Lagha, M., De Lillo, F. & Eckhardt, B. 2008 Laminar–turbulent boundary in plane Couette flow. Phys. Rev. E 78, 037301.CrossRefGoogle ScholarPubMed
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.Google Scholar
Smith, F. T. 1979 Instability of flow through pipes of general cross-section. Part 1. Mathematika 26, 187–210.Google Scholar
Smith, F. T. & Bodonyi, R. J. 1980 On the stability of the developing flow in a channel or circular pipe. Q. J. Mech. Appl. Maths 33, 293–320.CrossRefGoogle Scholar
Tillmark, N. 1995 On the spreading mechanisms of a turbulent spot in plane Couette flow. Europhys. Lett. 32, 481.Google Scholar
Tillmark, N. & Alfredsson, P. H. 1992 Experiments on transition in plane Couette flow. J. Fluid Mech. 235, 89–102.Google Scholar
van Veen, L. & Kawahara, G. 2011 Homoclinic tangle on the edge of shear turbulence. Phys. Rev. Lett. 107, 114501.CrossRefGoogle ScholarPubMed
Viswanath, D. 2009 The critical layer in pipe flow at high Reynolds number. Phil. Trans. R. Soc. A 367, 561–576.CrossRefGoogle ScholarPubMed
Waleffe, F. 1995 Hydrodynamic stability and turbulence: beyond transients to a self-sustaining process. Stud. Appl. Maths 95, 319–343.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81, 4140–4143.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Walton, A. G. 2002 The temporal evolution of neutral modes in the impulsively started flow through a circular pipe and their connection to the nonlinear stability of Hagen–Poiseuille flow. J. Fluid Mech. 457, 339–376.Google Scholar
Walton, A. G. 2004 Stability of circular Poiseuille–Couette flow to axisymmetric disturbances. J. Fluid Mech. 500, 169–210.Google Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98, 204501.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar
Willis, A. P. & Kerswell, R. R. 2009 Turbulent dynamics of pipe flow captured in a reduced model: puff relaminarization and localized ‘edge’ states. J. Fluid Mech. 619, 213–233.Google Scholar
Zuccher, S., Tumin, A. & Reshotko, E. 2006 Parabolic approach to optimal perturbations in compressible boundary layers. J. Fluid Mech. 556, 189–216.CrossRefGoogle Scholar