Article contents
Electrophoretic trajectories of non-uniformly charged particles in viscoelastic fluids: the weak surface charge limit
Published online by Cambridge University Press: 09 January 2023
Abstract
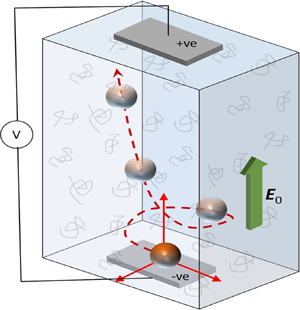
Electrophoretic motion of a particle carrying a weak but arbitrary non-uniform surface charge density in an Oldroyd-B fluid is analysed here in the thin electrical double layer limit. A semi-analytical generic framework, based on regular perturbation, the Lamb's general solutions and the generalized reciprocal theorem, assuming the viscoelastic effects to remain subdominant, is developed for tracing the particle's trajectory using its instantaneous translational velocity and accounting for the temporal evolution of its surface charge driven by rotation. Our results reveal that in a viscoelastic medium, non-uniformly charged particles may generally follow distinct trajectories depending on their sizes, which is in stark contrast to Newtonian fluids. By considering the multipole moments of the surface charge, we show that the particle may initially rotate until its dipole moment becomes collinear with the imposed electric field, and the nature of the surrounding medium does not alter this fundamental behaviour. However, during the course of rotation, the excess polymeric stresses within the electrical double layer and the bulk may cause the particle to migrate perpendicular to the applied field, by forcing the multipole moments of the surface charge to interact with each other. The final steady-state trajectory of the particle and its possible migration normal to the applied electric field are also largely governed by these interactions and more specifically, presence of non-zero quadrupole moments. The present framework may be helpful towards designing tools for particle separation and sorting, relevant in many biological applications.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by



