Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T18:35:35.407Z Has data issue: false hasContentIssue false
  • English
  • Français

The electrophoretic mobilities of a circular cylinder in close proximity to a dielectric wall

Published online by Cambridge University Press:  08 September 2016

Ehud Yariv
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In their bipolar-coordinate analysis of circular-cylinder electrophoresis near a dielectric wall, Keh et al. (J. Fluid Mech., vol. 231, 1991, pp. 211–228) found that, when an electric field is applied parallel to the wall, the translational and rotational electrophoretic mobilities increase monotonically as the ratio 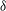$\unicode[STIX]{x1D6FF}$ of the cylinder–wall separation to the cylinder radius decreases, eventually diverging as 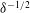$\unicode[STIX]{x1D6FF}^{-1/2}$ when 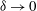$\unicode[STIX]{x1D6FF}\rightarrow 0$. Considering the singular limit 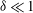$\unicode[STIX]{x1D6FF}\ll 1$ from the outset, we conduct here an asymptotic analysis of that electrokinetic problem, providing insight to the manner by which the intense electric field in the narrow gap is transformed into 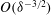$O(\unicode[STIX]{x1D6FF}^{-3/2})$ shear stresses; these stresses, in turn, overcome the large Stokes resistance so as to provide the large electrophoretic mobilities. In a companion problem, where the cylinder is exposed to a uniform current emanating from a nearby reactive electrode, the intense gap-scale electric field results in an 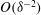$O(\unicode[STIX]{x1D6FF}^{-2})$ pressure, giving rise in turn to a large repulsive force. In that problem we find that the cylinder velocity perpendicular to the wall approaches a finite limit as 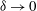$\unicode[STIX]{x1D6FF}\rightarrow 0$. We also discuss the role of ‘dielectrophoretic’ forces which are inevitable in the above semi-bounded configurations.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Lubrication theory
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , R5
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chen, S. B. & Keh, H. J. 1999 Boundary effects and particle interactions in electrophoresis. In Interfacial Forces and Fields (ed. Hsu, J.-P.), Surface Science Series, vol. 85, pp. 583–626. Marcel Dekker.Google Scholar
Crowdy, D. G. 2013 Wall effects on self-diffusiophoretic Janus particles: a theoretical study. J. Fluid Mech. 735, 473–498.Google Scholar
Crowdy, D. G. & Or, Y. 2010 Two-dimensional point singularity model of a low-Reynolds-number swimmer near a wall. Phys. Rev. E 81 (3), 036313.Google Scholar
Crowdy, D. & Samson, O. 2011 Hydrodynamic bound states of a low-Reynolds-number swimmer near a gap in a wall. J. Fluid Mech. 667, 309–335.Google Scholar
Dean, W. R. & O’Neill, M. E. 1963 A slow motion of a viscous liquid caused by the rotation of a solid sphere. Mathematika 10, 13–24.Google Scholar
Henry, D. C. 1931 The cataphoresis of suspended particles. Part I. The equation of cataphoresis. Proc. R. Soc. Lond. A 133 (821), 106–129.Google Scholar
Ibrahim, Y. & Liverpool, T. B. 2015 The dynamics of a self-phoretic Janus swimmer near a wall. Europhys. Lett. 111 (4), 48008.Google Scholar
Jeffrey, D. J. & Chen, H. S. 1977 The virtual mass of a sphere moving towards a plane wall. Trans. ASME J. Appl. Mech. 44, 166–167.CrossRefGoogle Scholar
Jeffrey, D. J. & Onishi, Y. 1981 The slow motion of a cylinder next to a plane wall. Q. J. Mech. Appl. Maths 34 (2), 129–137.Google Scholar
Keh, H. J. & Anderson, J. L. 1985 Boundary effects on electrophoretic motion of colloidal spheres. J. Fluid Mech. 153, 417–439.Google Scholar
Keh, H. J. & Chen, S. B. 1988 Electrophoresis of a colloidal sphere parallel to a dielectric plane. J. Fluid Mech. 194, 377–390.Google Scholar
Keh, H. J., Horng, K. D. & Kuo, J. 1991 Boundary effects on electrophoresis of colloidal cylinders. J. Fluid Mech. 231, 211–228.Google Scholar
Khair, A. S. 2013 Electrostatic forces on two almost touching nonspherical charged conductors. J. Appl. Phys. 114 (13), 134906.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.Google Scholar
Milne-Thomson, L. M. 1962 Theoretical Hydrodynamics, 4th edn. Macmillan.Google Scholar
Morrison, F. A. 1971 Transient electrophoresis of an arbitrarily oriented cylinder. J. Colloid Interface Sci. 36 (1), 139–145.Google Scholar
Morrison, F. A. & Stukel, J. J. 1970 Electrophoresis of an insulating sphere normal to a conducting plane. J. Colloid Interface Sci. 33 (1), 88–93.CrossRefGoogle Scholar
Mozaffari, A., Sharifi-Mood, N., Koplik, J. & Maldarelli, C. 2016 Self-diffusiophoretic colloidal propulsion near a solid boundary. Phys. Fluids 28 (5), 053107.CrossRefGoogle Scholar
O’Neill, M. E. 1964 A slow motion of a viscous liquid caused by a slowly moving solid sphere. Mathematika 11, 64–74.Google Scholar
Ristenpart, W. D., Aksay, I. A. & Saville, D. A. 2007 Electrically driven flow near a colloidal particle close to an electrode with a Faradaic current. Langmuir 23, 4071–4080.Google Scholar
Schnitzer, O. & Yariv, E. 2012 Macroscale description of electrokinetic flows at large zeta potentials: nonlinear surface conduction. Phys. Rev. E 86, 021503.Google ScholarPubMed
Stigter, D. 1978 Electrophoresis of highly charged colloidal cylinders in univalent salt solutions. 1. Mobility in transverse field. J. Phys. Chem. 82 (12), 1417–1423.CrossRefGoogle Scholar
Stone, H. A. 2005 On lubrication flows in geometries with zero local curvature. Chem. Engng Sci. 60 (17), 4838–4845.Google Scholar
Uspal, W. E., Popescu, M. N., Dietrich, S. & Tasinkevych, M. 2015 Self-propulsion of a catalytically active particle near a planar wall: from reflection to sliding and hovering. Soft Matt. 11 (3), 434–438.CrossRefGoogle Scholar
Wang, L. J. & Keh, H. J. 2011 Electrophoretic motion of a colloidal cylinder near a plane wall. Microfluid Nanofluid 10 (1), 81–95.Google Scholar
Yariv, E. 2006 ‘Force-free’ electrophoresis? Phys. Fluids 18, 031702.Google Scholar
Yariv, E. 2010a An asymptotic derivation of the thin-Debye-layer limit for electrokinetic phenomena. Chem. Engng Commun. 197, 3–17.Google Scholar
Yariv, E. 2010b Electro-hydrodynamic particle levitation on electrodes. J. Fluid Mech. 645, 187–210.CrossRefGoogle Scholar
Yariv, E. 2016a Dielectrophoretic sphere–wall repulsion due to a uniform electric field. Soft Matt. 12 (29), 6277–6284.Google Scholar
Yariv, E. 2016b Wall-induced self-diffusiophoresis of active isotropic colloids. Phys. Rev. Fluids 1 (3), 032101.Google Scholar
Yariv, E. & Brenner, H. 2003 Near-contact electrophoretic motion of a sphere parallel to a planar wall. J. Fluid Mech. 484, 85–111.Google Scholar
Yariv, E. & Schnitzer, O. 2013 Electrokinetic particle–electrode interactions at high frequencies. Phys. Rev. E 87 (1), 012310.Google ScholarPubMed