Electromagnetically driven flow in unsupported electrolyte layers: lubrication theory and linear stability of annular flow

Abstract

We consider a thin horizontal layer of a non-magnetic electrolyte containing a bulk solution of salt and carrying an electric current. The layer is bounded by two deformable free surfaces loaded with an insoluble surfactant and is placed in a vertical magnetic field. The arising Lorentz force drives the electrolyte in the plane of the layer. We employ the long-wave approximation to derive general two-dimensional hydrodynamic equations describing symmetric pinching-type deformations of the free surfaces. These equations are used to study the azimuthal flow in an annular film spanning the gap between two coaxial cylindrical electrodes. In weakly deformed films, the base azimuthal flow and its linear stability with respect to azimuthally invariant perturbations are studied analytically. For relatively thick layers and weak magnetic fields, the leading mode with the smallest decay rate is found to correspond to a monotonic azimuthal velocity perturbation. The Marangoni effect leads to further stabilisation of the flow while perturbations of the solute concentration in the bulk of the fluid have no influence on the flow stability. In strongly deformed films in the diffusion-dominated regime, the azimuthal flow becomes linearly unstable with respect to an oscillatory mixed mode characterised by the combination of radial and azimuthal velocity perturbations when the voltage applied between electrodes exceeds the critical value.

1. Introduction

Electromagnetically driven flows in shallow layers and channels of electrically conducting fluids in the presence of deformable interfaces have attracted much attention due to their importance in plasma physics (Fiflis et al. 2016; Lunz & Howell 2019) and various microfluidic applications including contactless manipulation of flow in magnetohydrodynamic (MHD) networks (Bau et al. 2003), liquid channels embedded into carrier fluids (Dunne et al. 2020), droplet microfluidics (Shang, Cheng & Zhao 2017) and electromagnetic stirring (Bau, Zhong & Yi 2001; Qian & Bau 2005).

The comprehensive theoretical description of MHD flows of magnetic fluid films in arbitrary strong magnetic fields is technically challenging as the hydrodynamic equations must be coupled with Maxwell's equations in the presence of deformable moving boundaries. However, in the case of non-magnetic electrically conducting fluids, the description can be greatly simplified. For this class of fluids, which comprises electrolyte solutions and liquid metals with weak magnetic properties, the additional stresses that typically appear at the interfaces due to externally applied magnetic fields can be neglected. For relatively weak magnetic fields of the order of $10^{-2}\unicode{x2013}10^0$ T, which can be created using conventional permanent magnets, the magnetic Reynolds number $\textit {Re}_m=UL/\eta _m$ associated with the flow of fluid with the magnetic diffusivity $\eta _m$ in the domain of a characteristic size $L$ with velocity $U$, is typically small, $\textit {Re}_m\ll 1$. In this regime the magnetic field induced by the electric current flowing through the fluid can be neglected compared with the external field (Müller & Bühler 2013). With this simplification, the MHD equations have been successfully applied to study flows of electrolitic solutions and non-magnetic liquid metals such as mercury in various geometries. These include liquid metal layers confined between two parallel insulating walls (Sommeria & Moreau 1982) and in thin horizontal films (Sommeria 1986) and electrolyte solutions in annular channels (Messadek & Moreau 2002; Figueroa et al. 2009; Pérez-Barrera, Ortiz & Cuevas 2016; Suslov, Pérez-Barrera & Cuevas 2017; McCloughan & Suslov 2020).

Geometric parameters of the system such as the depth and aspect ratio of the layer have been shown to have a major influence on the flow characteristics. In shallow horizontal layers of electrolyte solutions with a depth of several milimetres and a small depth-to-width aspect ratio placed between two coaxial vertical electrodes the flow was found to be essentially three-dimensional even for relatively weak currents (Figueroa et al. 2009; Pérez-Barrera et al. 2016; Suslov et al. 2017; McCloughan & Suslov 2020). The quasi-two-dimensional approximation, developed in Figueroa et al. (2009) and Pérez-Barrera et al. (2016) by using the depth-averaging method, could capture some of the main features of the base azimuthal flow but was shown to be inadequate when describing toroidal flows that lead to the formation of the experimentally observable free-surface vortices (Suslov et al. 2017).

As the depth of a horizontal layer and the aspect ratio of the system are further decreased, the vertical component of the flow velocity is impeded by the boundaries and the horizontal component of the flow becomes dominant. The two-dimensional nature of the flow in very thin liquid layers was used to study two-dimensional turbulence as pioneered around four decades ago by Couder (1981, 1984) in experiments with soap films that were mechanically stirred by an array of rods to produce a turbulent flow. At around the same time Sommeria (1986) studied effectively two-dimensional flows in thin mercury films with a free upper surface and supported from below by an array of conducting electrodes. Instead of a mechanical stirring, a contactless electromagnetic Lorentz forcing was used to drive the flow in the presence of highly non-uniform magnetic fields. Later, similar contactless electromagnetic forcing was used to gain a deeper understanding of the scaling properties of the velocity correlation function in turbulent regimes (Cardoso, Marteau & Tabeling 1994; Marteau, Cardoso & Tabeling 1995; Williams, Marteau & Gollub 1997). A comprehensive review of two-dimensional turbulence can be found, for example, in Kellay & Goldburg (2002).

Historically, electromagnetic driving was extensively used in supported liquid layers, but not in unsupported systems such as soap films. This, perhaps, was due to the intrinsic instability of soap-type films and the difficulty of controlling their curvature. In fact, to the best of our knowledge, the first attempt to use Lorentz force in unsupported free films was made almost 20 years after Couder (1981, 1984) pioneered the film turbulence studies. It used a soap film containing chloride salt spanning a region between two parallel conducting electrodes placed above an array of permanent magnets (Rivera & Wu 2000). The main advantage of using an unsupported film when studying two-dimensional turbulence is the elimination of energy leakage at the no-slip bottom of the container. In a recent experimental study, Cruz Gómez (2016) investigated the flow dynamics in an electromagnetically forced film in the case of a localised source of electric current. A series of experiments with soap films spanning the gap between two coaxial electrodes placed in an external magnetic field is currently under way (S. Cuevas & A. Figueroa, personal communication 2023).

The theoretical description and modelling of electromagnetically driven flows in supported films with a free interface are now well developed (Morley & Abdou 1995; Morley & Roberts 1996; Morley & Abdou 1997; Gao & Morley 2002; Gao, Morley & Dhir 2002; Morley, Smolentsev & Gao 2002; Miloshevsky & Hassanein 2010; Giannakis, Fischer & Rosner 2009a; Giannakis, Rosner & Fischer 2009b; Lunz & Howell 2019) and continue to attract attention mainly due to applications in plasma flows and tokamaks. In the absence of the Lorentz force, the pure hydrodynamic description of the flow in unsupported liquid films was initiated in Prévost & Gallez (1986), Sharma & Ruckenstein (1988) and later received a huge boost because of its relevance to nonlinear film rupture and two-dimensional turbulence problems (Couder, Chomaz & Rabaud 1989; Gharib & Derango 1989; Chomaz & Cathalau 1990; Erneux & Davis 1993; Sharma et al. 1995; Van De Fliert, Howell & Ockenden 1995; Wu et al. 1995) as reviewed in Kellay & Goldburg (2002) and Oron, Davis & Bankoff (1997). In unsupported thin viscous films the hydrodynamic equations are simplified using two main assumptions. Firstly, the long-wave approximation is applied by taking into account large-scale flow patterns and film deformations, the wavelength of which is much larger than the average film thickness. Secondly, deformations of the free interfaces are assumed to be mirror symmetric with respect to the centre plane of the layer, which corresponds to a varicose-type pinching deformation mode. Under these assumptions, the effective two-dimensional dynamic equations were derived at the leading order of the lubrication approximation for curved soap films in the presence of a surfactant (Ida & Miksis 1998; Miksis & Ida 1998) and for horizontally stretched free films in the presence of solute and surfactant (Chomaz 2001). So far, the application of the lubrication approximation to describe MHD flows in unsupported free films of electrolyte solutions in external magnetic fields has not been reported.

Here we build upon earlier theoretical studies (Ida & Miksis 1998; Miksis & Ida 1998; Chomaz 2001) to derive the leading-order dynamic equations for an electromagnetically driven two-dimensional flow in a thin free horizontal layer of electrolyte solution the free surfaces of which are loaded with an insoluble surfactant. The flow is driven by the Lorentz force generated by the electric current flowing through the electrolyte in the presence of a homogeneous external magnetic field normal to the layer. We show that at the leading order of the lubrication approximation the product of the current density and the local thickness of the layer is divergence free reflecting the condition of no accumulation of electric charge in the bulk. The complete set of the derived dynamic equations is written in an invariant vector form suitable for applications in arbitrary geometries. It consists of the dynamic equation for the two-dimensional flow field depending on the solute concentration in the bulk, surfactant concentration, symmetric film deformations and the electric potential. As an example, we apply the derived equations to study the azimuthal flow and its linear stability in annular free films spanning the gap between two coaxial conducting electrodes.

The paper is organised as follows. In § 2 we present the derivation of the leading-order equations in the lubrication approximation using the systematic expansion technique suggested earlier in Erneux & Davis (1993) and Chomaz (2001). The derived equations correctly reflect the conservation of the total mass of the surfactant and solute as well as the continuity of electric current under the condition of no accumulation of the electric charge in the fluid. In § 3 we rewrite the derived equations in polar coordinates to study the flow in annular free films. In § 4 we study the linear stability of the annular azimuthally invariant steady state with respect to perturbations that depend only on the radial coordinate. We present analytical results for the linear stability of a flat film and vanishingly small flow velocities first. Subsequently, we use the numerical continuation method (Krauskopf, Osinga & Galan-Vioque 2014; Doedel, Wang & Fairgrieve 1994) to study the stability of a strongly deformed layer. The obtained theoretical and computational results are summarised in § 5.

2. Lubrication theory of electrically conducting free films in an external magnetic field

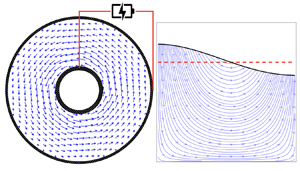
Consider a horizontal free film of an electrolyte solution, which can be created by supporting the weight of the film by the pressure difference between the regions below and above the film. Following Erneux & Davis (1993) and Chomaz (2001) we exclude film bending and only consider symmetric pinching-type surface deformation modes $z=\pm h(x,y,t)$ with each surface being a mirror image of the other at all times as schematically shown in figure 1(a). Here, $x$ and $y$ are the coordinates in the horizontal plane, $z$ is a vertical coordinate and $t$ is time. The local thickness of the film is $2h$ and the average film thickness is

(2.1)\begin{equation} 2\langle h\rangle=2S^{-1}\int_S h(x,y,t)\,{{\rm d}\kern0.06em x}\,{{\rm d}y}, \end{equation}

where $S$ denotes the area of the centre plane $z=0$.

Figure 1. ($a$) Symmetric deformation mode in a horizontal free liquid film with two deformable surfaces located at $z=\pm h(x,y,t)$. The flow field $\boldsymbol {u}=(u,v,w)$ is mirror symmetric with respect to the centre plane $z=0$. (b–e) The top view of the system: four possible topological configurations of a free film spanning space between two electrodes $(1,2)$. The surface of each electrode $\partial \varSigma$ represents a no-slip equipotential boundary impenetrable for surfactant and electrolyte solution.

Our focus on symmetric film surface deformations is prompted by the observation that in the absence of a pressure difference across the film and in the case of symmetrical boundary conditions for the lower and the upper interfaces, the squeezing deformation mode is expected to be the least stable (Erneux & Davis 1993; Chomaz 2001). Note however that non-symmetric deformations may become dominant in the transient nonlinear regimes. In the absence of the Lorentz force, the general set of the leading-order equations in the lubrication approximation that takes into account both symmetric and non-symmetric deformations was formulated in Ida & Miksis (1998). However, all subsequent applications of their general theory including stability of planar films and spherical bubbles were discussed for symmetric deformation modes (Miksis & Ida 1998; Chomaz 2001).

Each surface of the film is loaded with an insoluble surfactant with local concentration $c_s$. The addition of surfactants is particularly important in soap films that contain fatty acid carboxylates, which are typically found at the surface. The electrolyte solution is composed of a solvent fluid (typically pure water) and dissociated salt molecules with bulk concentration $c_b$. In what follows we assume that salt is completely soluble and does not form a molecular surface layer. Two electrodes are immersed in the fluid so that the electric current can flow between them through the film when external voltage is applied. One may consider at least four possible topological configurations of a free film spanning space between two electrodes as shown in figures 1(b)–1(e). The surface of the electrodes $\partial \varSigma$ is assumed to be chemically inert and impenetrable to the surfactant and the solute in the film. In addition, the flow field $\boldsymbol {u}$ vanishes at $\partial \varSigma$.

The electrical conductivity $\sigma$ of the electrolyte solution generally depends on $c_b$. The solution density $\rho$ and dynamic viscosity $\mu$ (kinematic viscosity $\nu =\mu /\rho$) are assumed to be constant and independent of $c_b$. The externally applied magnetic field ${\boldsymbol {B}}=(0,0,B(x,y))$ is assumed to be significantly stronger than that induced by the motion of the fluid. In what follows we neglect gravity effects anticipating that hydrostatic pressure in a submicrometre thin free film is negligible as compared with the Laplace pressure. The motion of the incompressible fluid with three-dimensional velocity ${\boldsymbol {u}}=(u,v,w)$ is described by the continuity and Navier–Stokes equations with the added Lorentz force term (Müller & Bühler 2013)

(2.2)$$\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{u}}=0, \end{gather}$$

(2.3)$$\begin{gather}\partial_t{\boldsymbol{u}}+({\boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}){\boldsymbol{u}}=-\frac{1}{\rho}\boldsymbol{\nabla} (\,p-\varPi) +\frac{\mu}{\rho}\nabla^2{\boldsymbol{u}}+\frac{1}{\rho}{\boldsymbol{j}}\times{\boldsymbol{B}}, \end{gather}$$

where $p$ is the pressure in the fluid and $\varPi =\varPi (h(x,y,t))$ represents the disjoining pressure due to intermolecular forces that become important when the film thickness is approximately 100 nm or less (Overbeek 1960; Israelachvili 2011). Because of the symmetry of the pinching mode, the horizontal flow velocity components $(u,v)$ and the vertical velocity component $w$ should be an even and odd function of $z$, respectively.

The current density ${\boldsymbol {j}}=(\,j_x,j_y,j_z)$ is related to the electric potential $\phi$ via Ohm's law

(2.4)\begin{equation} {\boldsymbol{j}}=\sigma(c_b) (-\boldsymbol{\nabla}\phi+{\boldsymbol{u}}\times{\boldsymbol{B}}).\end{equation}

For electrolyte solutions, we assume linear dependence between conductivity $\sigma$ and $c_b$,

(2.5)\begin{equation} \sigma(c_b)=Kc_b,\end{equation}

where $K$ is an empirical constant specific to a particular salt and solvent. Under the condition of no accumulation of electric charge in the bulk, the electric potential $\phi$ is found from

(2.6)\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{j}}=0,\end{equation}

which must be solved instantaneously for any given velocity field ${\boldsymbol {u}}$. Additionally, the current continuity condition (2.6) must be supplemented with the boundary conditions for $\phi$ that correspond to the equipotential surfaces $\partial \varSigma$ of the conducting electrodes.

Note that for a magnetic field ${\boldsymbol {B}}=(0,0,B)$ orthogonal to the layer ${\boldsymbol {j}}\times {\boldsymbol {B}}=B(\,j_y,-j_x,0)$, ${\boldsymbol {j}}=\sigma (c_b)(-\partial _x\phi +Bv,-\partial _y\phi -Bu,-\partial _z\phi )$ and ${\boldsymbol {u}}\times {\boldsymbol {B}}=B(v,-u,0)$. The normal component of the electric current vanishes at the film surfaces. Thus, at $z=h$ we require

(2.7)\begin{equation} j_n={\boldsymbol{j}}\boldsymbol{\cdot}{\boldsymbol{n}}=0,\end{equation}

where ${\boldsymbol {n}}=(-\partial _xh,-\partial _yh,1) /\sqrt {1+(\partial _x h)^2+(\partial _y h)^2}$ is the unit normal vector to the upper film surface directed away from the fluid.

At $z=h$, the kinematic boundary condition applies, i.e.

(2.8)\begin{equation} \partial_t h+({\boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}_\parallel)h=w,\end{equation}

where $\boldsymbol {\nabla }_\parallel =(\partial _x,\partial _y)$ is the horizontal gradient. Note that (2.8) can also be written in the equivalent form as $\partial _t h=\sqrt {1+(\boldsymbol {\nabla }_\parallel h)^2}({\boldsymbol {n}}\boldsymbol {\cdot }{\boldsymbol {u}})$.

To describe the dynamics of surfactant and the concentration of salt in the bulk of the fluid, we follow Jensen & Grotberg (1993). The bulk concentration $c_b$ is described by the advection–diffusion equation

(2.9)\begin{equation} \partial_tc_b+\boldsymbol{\nabla}\boldsymbol{\cdot}({\boldsymbol{u}} c_b-d_b\boldsymbol{\nabla} c_b)=0,\end{equation}

where $d_b$ is the bulk diffusion coefficient, ${\boldsymbol {u}} c_b$ is the advective flux and $-d_b\boldsymbol {\nabla } c_b$ is the diffusive flux.

The advection–diffusion equation for the surfactant concentration at the upper film surface $z=h(x,y,t)$ is given by

(2.10)\begin{equation} \partial_t c_s+\boldsymbol{\nabla}_s\boldsymbol{\cdot}(c_s{\boldsymbol{u}})=d_s\boldsymbol{\nabla}_s^2c_s,\end{equation}

where $d_s$ is the surface diffusivity of the surfactant and $\boldsymbol {\nabla }_s=\boldsymbol {\nabla }-{\boldsymbol {n}}({\boldsymbol {n}}\boldsymbol {\cdot }\boldsymbol {\nabla })$ is the surface gradient.

At $z=h$ the diffusive flux normal to the film surface must vanish, i.e.

(2.11)\begin{equation} {\boldsymbol{n}}\boldsymbol{\cdot}\boldsymbol{\nabla} c_b=0.\end{equation}

It can be shown that (2.11) supplemented with the condition that the flow velocity ${\boldsymbol {u}}$ and the normal diffusive fluxes of surfactant and solute vanish at the surface of the electrodes leads to the conservation of the total mass of the solute and the surfactant.

Next, we consider the balance of the normal and tangential forces at the upper surface $z=h(x,y,t)$:

(2.12)\begin{equation} (\,p+\varGamma\kappa){\boldsymbol{n}}=\boldsymbol{\nabla}_s\varGamma+{\boldsymbol{\mathsf{T}}}\boldsymbol{\cdot}{\boldsymbol{n}}.\end{equation}

Here, ${\boldsymbol{\mathsf{T}}}=\mu [\boldsymbol {\nabla }\otimes {\boldsymbol {u}}+(\boldsymbol {\nabla }\otimes {\boldsymbol {u}})^{\rm T}]$ is the viscous stress tensor, $\kappa (x,y,t)$ is the local mean curvature of the surface defined as $\kappa =-\boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol {n}}$, $\varGamma (x,y,t)$ is the local surface tension, $\otimes$ is the tensor product and the superscript T denotes transposed quantities. In what follows we assume that the liquid is non-magnetic and the applied magnetic field is relatively weak so that the Maxwell component in the stress tensor can be completely neglected.

The gradient of the surface tension along the interface $\partial _s\varGamma$ is induced by the distribution of the surfactant according to the soluto-Marangoni effect

(2.13)\begin{equation} \varGamma(x,y,t)=\gamma-\varGamma_Mc_s(x,y,t),\end{equation}

where $\gamma$ is the reference surface tension in the absence of a surfactant and $\varGamma _M=-{\rm d}\varGamma /{\rm d}c_s>0$ is assumed to be constant. The balance of forces at the lower surface $z=-h(x,y,t)$ is automatically achieved for symmetric deformation modes. Note that in the case of a nonlinear dependence of the surface tension on the surfactant concentration, the coefficient $\varGamma _M$ is concentration dependent. Such a nonlinear equation of state may lead to different physical outcomes and would require a separate study.

The horizontal length scale $L$ of the flow in submicrometre thin films is several orders of magnitude larger than the average film thickness $2\langle h\rangle$. The long-wave approximation theory of one-dimensional free films in the absence of a surfactant and an electric current was developed some 30 years ago (Erneux & Davis 1993) using systematic expansion of the Navier–Stokes equations for a small lubrication parameter $\epsilon =\langle h\rangle /L \ll 1$. Subsequently, the theory was generalized to describe two-dimensional flat and curved free films loaded with soluble and insoluble surfactant agents (Ida & Miksis 1998; Miksis & Ida 1998; Chomaz 2001). Here we extend earlier results to derive the leading-order equations for long-wave symmetric deformations of a free electrically conducting film placed in an external magnetic field.

We scale horizontal coordinates $(x,y)$ with $L$ and the vertical coordinate $z$ and the local interface deflection $h(x,y,t)$ with $\langle h\rangle =\epsilon L$. The horizontal fluid velocity $(u,v)$ is scaled with some reference velocity $U=O(1)$, the vertical velocity $w$ with $\epsilon U=O(\epsilon )$, time with $L/U=O(1)$ and the pressure and the disjoining pressure with $\rho U^2$. The magnetic field $B(x,y)$ is non-dimensionalised using some reference value ${\tilde {B}}$ while the scaling for the electric potential is $U\tilde {B}L$. The bulk salt and the surface surfactant concentrations are scaled using arbitrary reference concentrations $c_b^{(0)}$ and $c_s^{(0)}$, respectively, so that the conductivity $\sigma (c_b)$ is scaled with $Kc_b^{(0)}$. The dimensionless bulk equations (2.2), (2.3), (2.6) and (2.9) then become

(2.14)\begin{gather} \partial_xu+\partial_yv+\partial_z w =0,\end{gather}

(2.15) \begin{align} \partial_tu+(u\partial_x+v\partial_y+w\partial_z)u &=-\partial_x[\,p-\varPi] +\textit{Re}^{-1}\left(\partial_x^2+\partial_y^2+\epsilon^{-2}\partial_z^2\right)u\nonumber\\ &\quad -\textit{Ha}^2\,\textit{Re}^{-1}c_bB(Bu+\partial_y\phi), \end{align}

(2.16) \begin{align} \partial_tv+(u\partial_x+v\partial_y+w\partial_z)v&=-\partial_y[\,p-\varPi] +\textit{Re}^{-1}\left(\partial_x^2+\partial_y^2+\epsilon^{-2}\partial_z^2\right)v\nonumber\\ &\quad -\textit{Ha}^2\,\textit{Re}^{-1}c_bB(Bv-\partial_x\phi), \end{align}

(2.17)\begin{gather} \partial_t w+(u\partial_x+v\partial_y+w\partial_z)w =-\epsilon^{-2}\partial_z p+\textit{Re}^{-1}\left(\partial_x^2+\partial_y^2+\epsilon^{-2}\partial_z^2\right)w, \end{gather}

(2.18)\begin{gather} \partial_x[c_b(Bv-\partial_x\phi)] -\partial_y[c_b(Bu+\partial_y\phi)] -\epsilon^{-2}\partial_z[c_b\partial_z\phi]=0,\end{gather}

(2.19)\begin{gather} \partial_tc_b+u\partial_xc_b+v\partial_yc_b+w\partial_zc_b =\textit{Sc}^{-1}\,\textit{Re}^{-1} \left(\partial_x^2+\partial_y^2+\epsilon^{-2}\partial_z^2\right)c_b, \end{gather}

where we used the same notations for the dimensionless quantities and introduced the Reynolds ($\textit {Re}$), Hartmann ($\textit {Ha}$), Péclet ($\textit {Pe}$) and Schmidt ($\textit {Sc}$) numbers defined as

(2.20a–d)\begin{equation} \textit{Re}=\frac{UL\rho}{\mu},\quad \textit{Ha}^2 =\frac{{\tilde{B}}^2L^2Kc_b^{(0)}}{\mu},\quad \textit{Pe}=\frac{LU}{d_s},\quad \textit{Sc}=\frac{\mu}{\rho d_b}.\end{equation}

From (2.12), the dimensionless normal and the tangential balances of stresses at $z=h$ are given by

(2.21)\begin{gather} p+ (\textit{Ca}\,\textit{Re})^{-1}\left(\partial_x^2h+\partial_y^2h\right) =2\,\textit{Re}^{-1}\left(\partial_zw-\partial_xh\partial_zu -\partial_yh\partial_zv\right)+O(\epsilon^2),\end{gather}

(2.22) \begin{align} -\textit{Ma}\textit{Pe}^{-1}\partial_xc_s &=\epsilon^{-2} \partial_zu+\left[\vphantom{(\partial_xh)^2\partial_zu-\partial_xh\,\partial_yh\partial_zv +2\partial_xh\partial_zw}-2\partial_xh\partial_xu -\partial_yh(\partial_yu+\partial_xv)+\partial_xw\right.\nonumber\\ &\quad-\left.(\partial_xh)^2\partial_zu-\partial_xh\partial_yh\partial_zv +2\partial_xh\partial_zw\right]+O(\epsilon^2), \end{align}

(2.23) \begin{align} -\textit{Ma}\textit{Pe}^{-1}\partial_yc_s &=\epsilon^{-2}\partial_zv+\left[\vphantom{(\partial_xh)^2\partial_zu-\partial_xh\,\partial_yh\partial_zv +2\partial_xh\partial_zw} -2\partial_yh\partial_yu -\partial_xh(\partial_xv+\partial_yu)+\partial_yw\right. \nonumber\\ &\quad -\left.(\partial_yh)^2\partial_zv-\partial_xh\partial_yh\partial_zv +2\partial_yh\partial_zw\right]+O(\epsilon^2), \end{align}

with the capillary ($\textit {Ca}$) and Marangoni ($\textit {Ma}$) numbers defined as

(2.24a,b)\begin{equation} \textit{Ca}=\frac{\mu UL}{\langle h\rangle\gamma},\quad \textit{Ma}=\frac{c_s^{(0)}\varGamma_ML^2}{\langle h\rangle\mu d_s}. \end{equation}

The scaled boundary condition for the electric current (2.7), the kinematic condition (2.8), the surfactant equation (2.10) and (2.11) multiplied by $\sqrt {1+(\partial _xh)^2+(\partial _y h)^2}$ are given by

(2.25)$$\begin{gather} 0=(\partial_x\phi-Bv)\partial_x h +(\partial_y\phi-Bu) \partial_y h +\epsilon^{-2}\partial_z\phi, \end{gather}$$

(2.26)$$\begin{gather}\partial_th =-u\partial_xh-v\partial_yh+w, \end{gather}$$

(2.27)$$\begin{gather}\partial_tc_s =-\partial_x[uc_s]-\partial_y[vc_s] +\textit{Pe}^{-1}\left(\partial_x^2+\partial_y^2\right)c_s +O\left(\epsilon^2\right)\!, \end{gather}$$

(2.28)$$\begin{gather}0=\partial_xh\partial_xc_b+\partial_yh\partial_yc_b -\epsilon^{-2}\partial_zc_b. \end{gather}$$

Crucial for further analysis is to determine the order of magnitude of all dimensionless parameters appropriate for the physical regime of interest. Following Chomaz (2001) we assume that, for free liquid films, the inertial effects play an essential role implying that $\textit {Re}=O(1)$. The leading contribution to pressure in the fluid is anticipated to come from the Laplace pressure, which implies that $\textit {Ca}=O(1)$. Note that, for example, for slipper bearing flows and liquid films on a solid substrate, the capillary number scales as $\textit {Ca}=(U\mu /\gamma )\epsilon ^{-3}=O(1)$ (Oron et al. 1997). We assume that the Marangoni effect is weak so that at the leading order the film surfaces can be considered stress free (Chomaz 2001). This can be achieved by setting $\textit {Ma}=O(1)$. An additional assumption must be made regarding the strength of the magnetic field and the induced electric current. Here we consider weakly conducting electrolytes in weak magnetic fields and assume that the Lorentz force is of the same order of magnitude as the viscous force in the absence of vertical shear, i.e. $\boldsymbol {\nabla }_\parallel ^2u\sim \textit {Ha}^2\boldsymbol {\nabla }_\parallel \phi$. This implies that $\textit {Ha}=O(1)$.

All fields in (2.14)–(2.28) are then expanded into a series in powers of $\epsilon ^2$, e.g. $u=u_0+\epsilon ^2u_1+\ldots$ with $u_i=O(1)$, and the leading zero-order equations are derived by following the procedure outlined in Erneux & Davis (1993) and Chomaz (2001). At the zeroth order, the equations for $h_0$, $u_0$, $v_0$, $w_0$, $p_0$ and $(c_{s})_0$ are identical to those derived in Chomaz (2001) as the Lorentz force enters the equations only at the next order. Therefore, $u_0$, $v_0$ and $p_0$ are independent of $z$ and $w_0=-(\partial _x u_0+\partial _y v_0)z$.

At the leading order, from (2.18) and (2.19) we obtain for the electric potential $\phi _0$ and the bulk concentration $(c_{b})_0$,

(2.29a,b)\begin{equation} \partial_z[(c_b)_0\,\partial_z\phi_0]=0,\quad \partial_z^2(c_{b})_0=0.\end{equation}

Since $\partial _z\phi _0=\partial _z(c_{b})_0=0$ at $z=h_0$, from (2.25) and (2.28) we conclude that both $(c_{b})_0$ and $\phi _0$ are independent of $z$.

The surfactant concentration $(c_{s})_0$ satisfies the two-dimensional advection–diffusion equation

(2.30)\begin{equation} \partial_t(c_s)_0+\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}[(c_s)_0{\boldsymbol{u}}_0] =\textit{Pe}^{-1}\boldsymbol{\nabla}_\parallel^2(c_s)_0,\end{equation}

where ${\boldsymbol {u}}_0=(u_0,v_0)$ is the leading-order horizontal velocity. The kinematic equation (2.26) together with $w_0(z=h_0)=-(\boldsymbol {\nabla }_\parallel \boldsymbol {\cdot }{\boldsymbol {u}}_0)h_0$ yield the evolution equation for the local film deformation

(2.31)\begin{equation} \partial_th_0+\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}[h_0u_0]=0.\end{equation}

At the next order, the Navier–Stokes equations for the horizontal flow contain the Lorentz force terms

(2.32)\begin{align} \partial_tu_0+(u_0\partial_x+v_0\partial_y)u_0 &=-\partial_x[\,p_0-\varPi_0] +\textit{Re}^{-1}\left(\partial_x^2+\partial_y^2\right)u_0\nonumber\\ &\quad-\textit{Ha}^2\,\textit{Re}^{-1}(c_b)_0B_0({B_0}u_0+\partial_y\phi_0 +\textit{Re}^{-1}\partial_z^2u_2, \end{align}

(2.33)\begin{align} \partial_t v_0+(u_0\partial_x+v_0\partial_y)v_0 &=-\partial_y[\,p_0-\varPi_0] +\textit{Re}^{-1}\left(\partial_x^2+\partial_y^2\right)v_0\nonumber\\ &\quad -\textit{Ha}^2\,\textit{Re}^{-1}(c_b)_0B_0({B_0}v_0-\partial_x\phi_0) +\textit{Re}^{-1}\partial_z^2v_2, \end{align}

where the electric potential $\phi _2$ satisfies the equation

(2.34)\begin{equation} \partial_x[(c_{b})_0(B_0v_0-\partial_x\phi_0)] -\partial_y[(c_b)_0(B_0u_0+\partial_y\phi_0)] +(c_{b})_0\partial_z^2\phi_2=0.\end{equation}

The boundary condition for $\phi _2$ at the film surface $z=h_0$ obtained from (2.25) is

(2.35)\begin{equation} \partial_z\phi_2=(B_0u_0+\partial_y\phi_0)\partial_yh_0 -(B_0v_0-\partial_x\phi_0)\partial_xh_0.\end{equation}

Equation (2.34) shows that $\phi _2$ is a quadratic function of $z$,

(2.36)\begin{equation} \phi_2=A(x,y)z^2+B(x,y)z+C(x,y),\end{equation}

Since for symmetric deformations the potential $\phi$ must be an even function of $z$, we set $B(x,y)=0$ and determine $A(x,y)$ from the boundary condition (2.35) to obtain

(2.37)\begin{equation} \phi_2=-\frac{[(B_0v_0-\partial_x\phi_0)\partial_xh_0 -(B_0u_0+\partial_y\phi_0)\partial_yh_0]z^2}{2h_0} +C(x,y).\end{equation}

Finally, substituting (2.37) into (2.34) we obtain

(2.38)\begin{align} &\partial_x[(c_{b})_0(B_0v_0-\partial_x\phi_0)] -\partial_y[(c_{b})_0(B_0u_0+\partial_y\phi_0)]\nonumber\\ &\quad +\frac{(c_{b})_0[(B_0v_0-\partial_x\phi_0)\partial_xh_0 -(B_0u_0+\partial_y\phi_0)\partial_yh_0]}{h_0}=0. \end{align}

Multiplying (2.38) by $h_0$ and introducing the current ${\boldsymbol {j}}_0=(c_b)_0({\boldsymbol {u}}_0\times {\boldsymbol {B}}_0-\boldsymbol {\nabla }_\parallel \phi _0)$ we rewrite (2.38) in an invariant vector form,

(2.39)\begin{equation} \boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}(h_0\,{\boldsymbol{j}}_0)=0.\end{equation}

Equation (2.39) represents the continuity equation for the electric current per unit length of the cross-section of the film.

Next, we eliminate $u_2$ and $v_2$ from (2.33) by taking into account the boundary conditions for the tangential and normal components of the stress tensor at $z=h_0$. Because the electromagnetic component of the viscous stress tensor is neglected here, the result of the elimination procedure is identical to that of Chomaz (2001). Consequently, we arrive at the leading-order dynamic equation for ${\boldsymbol {u}}_0$ including the Lorentz force

(2.40)\begin{align} \partial_t{\boldsymbol{u}}_0 +({\boldsymbol{u}}_0\boldsymbol{\cdot}\boldsymbol{\nabla}_\parallel){\boldsymbol{u}}_0 &=\dfrac{\textrm{d}\varPi_0}{\textrm{d}h_0}\boldsymbol{\nabla}_\parallel h_0 +(\textit{Ca}\,\textit{Re})^{-1}\boldsymbol{\nabla}_\parallel\boldsymbol{\nabla}_\parallel^2h_0 +3\,\textit{Re}^{-1}\boldsymbol{\nabla}_\parallel(\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}{\boldsymbol{u}}_0)\nonumber\\ &\quad +\textit{Re}^{-1}\boldsymbol{\nabla}_\parallel^2{\boldsymbol{u}} -\frac{(\textit{Re}\,\textit{Pe})^{-1}\,\textit{Ma}}{h_0}\boldsymbol{\nabla}_\parallel(c_{s})_0 +\frac{\textit{Re}^{-1}}{h_0}{\boldsymbol{V}}\nonumber\\ &\quad +\textit{Ha}^2\,\textit{Re}^{-1}{\boldsymbol{j}}_0\times{\boldsymbol{B}}_0, \end{align}

where we replaced the vector $(c_b)_0B_0[(-\partial _y\phi _0,\partial _x\phi _0)-B_0{\boldsymbol {u}}_0]$ with ${\boldsymbol {j}}_0\times {\boldsymbol {B}}_0$ and introduced an additional flow field

(2.41)\begin{equation} {\boldsymbol{V}}=2(\boldsymbol{\nabla}_\parallel h_0\boldsymbol{\cdot}\boldsymbol{\nabla}_\parallel){\boldsymbol{u}}_0 +\boldsymbol{\nabla}_\parallel h_0\times(\boldsymbol{\nabla}_\parallel{\times}{\boldsymbol{u}}_0) +2\boldsymbol{\nabla}_\parallel h_0(\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}{\boldsymbol{u}}_0)\end{equation}

that can be associated with the so-called extensional Trouton viscosity.

To close the system of leading-order dynamic equations, we derive the equation for the bulk concentration $(c_b)_0$. At the leading order, from (2.29a,b) we see that $(c_b)_0$ is independent of $z$. At the next order, from (2.19) we obtain

(2.42)\begin{align} \partial_t(c_b)_0+u_0\partial_x(c_b)_0+v_0\partial_y(c_b)_0 =\textit{Sc}^{-1}\,\textit{Re}^{-1}(\partial_x^2+\partial_y^2)(c_b)_0 +\textit{Sc}^{-1}\,\textit{Re}^{-1}\partial_z^2(c_b)_2.\end{align}

The boundary condition at $z=h_0$ following from (2.28) reads

(2.43)\begin{equation} \partial_z(c_b)_2=\partial_xh_0\partial_x(c_b)_0 +\partial_yh_0\partial_y(c_b)_0.\end{equation}

For a symmetric mode and according to (2.42), the field $(c_b)_2$ is a quadratic function of $z$: $(c_b)_2=a(x,y,t)z^2+c(x,y,t)$. Applying (2.43) we write

(2.44)\begin{equation} (c_b)_2=\frac{\partial_xh_0\partial_x(c_b)_0 +\partial_yh_0\partial_y(c_b)_0}{2h_0}z^2 +c(x,y,t).\end{equation}

Substituting (2.44) into (2.42) we obtain

(2.45)\begin{align} \partial_t(c_b)_0 +u_0\partial_x(c_b)_0+v_0\partial_y(c_b)_0 &=\textit{Sc}^{-1}\,\textit{Re}^{-1}(\partial_x^2+\partial_y^2)(c_b)_0\nonumber\\ &\quad +\textit{Sc}^{-1}\,\textit{Re}^{-1}\frac{\partial_xh_0\partial_x(c_b)_0 +\partial_yh_0\partial_y(c_b)_0}{h_0}. \end{align}

Multiplying (2.45) by $h_0$ and using the kinematic condition (2.31) we arrive at

(2.46)\begin{equation} \partial_t [h_0(c_b)_0] +\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}[h_0{\boldsymbol{u}}_0(c_b)_0] =\textit{Sc}^{-1}\,\textit{Re}^{-1}\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}[h_0\boldsymbol{\nabla}_\parallel (c_b)_0].\end{equation}

Equation (2.46) is identical to the transport equation for the solute concentration obtained at the leading order of the lubrication approximation after averaging over the film cross-section that was derived in Jensen & Grotberg (1993). It generalizes the leading-order equation for the bulk concentration derived in Chomaz (2001) to the case of large film deformations.

We summarise our results by writing the complete set of dimensional governing equations using physical variables and parameters:

(2.47)\begin{equation} \left.\begin{gathered} \rho(\partial_t{\boldsymbol{u}}+({\boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}_\parallel){\boldsymbol{u}}) =g(h)\boldsymbol{\nabla}_\parallel h +\gamma\boldsymbol{\nabla}_\parallel\boldsymbol{\nabla}_\parallel^2h +\mu\boldsymbol{\nabla}_\parallel^2{\boldsymbol{u}}+3\mu\boldsymbol{\nabla}_\parallel (\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}{\boldsymbol{u}})\\ \quad-\frac{\varGamma_M}{h}\boldsymbol{\nabla}_\parallel c_s+\frac{\mu{\boldsymbol{V}}}{h}+{\boldsymbol{j}}\times{\boldsymbol{B}},\\ {\boldsymbol{V}} =2(\boldsymbol{\nabla}_\parallel h \cdot \boldsymbol{\nabla}_\parallel){\boldsymbol{u}} +\boldsymbol{\nabla}_\parallel h\times (\boldsymbol{\nabla}_\parallel{\times}{\boldsymbol{u}}) +2\boldsymbol{\nabla}_\parallel h(\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}{\boldsymbol{u}}),\\ \boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}(h{\boldsymbol{j}})=0,\\ {\boldsymbol{j}}=Kc_b[{\boldsymbol{u}}\times{\boldsymbol{B}}-\boldsymbol{\nabla}_\parallel\phi],\\ \partial_t h=-\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}(h{\boldsymbol{u}}),\\ \partial_t(h c_b)=-\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}(hc_b{\boldsymbol{u}}) +d_b\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot}(h\boldsymbol{\nabla}_\parallel c_b),\\ \partial_tc_s=-\boldsymbol{\nabla}_\parallel\boldsymbol{\cdot} (c_s{\boldsymbol{u}})+d_s\boldsymbol{\nabla}_\parallel^2c_s. \end{gathered}\right\}\end{equation}

Here we introduced function $g(h)=\textrm {d}\varPi (h)/\textrm {d}h$ and dropped subscript $0$. In the case of soluble surfactants, an additional bulk concentration field must be introduced the dynamics of which is described by the reaction–diffusion equation including the sorption–desorption fluxes (Chomaz 2001). Note that (2.47) are written in a compact vector form, which is invariant with respect to the choice of a coordinate system. This is especially important in applications with non-rectangular geometry as exemplified in the next section.

3. Azimuthal flow in an annular free film between two coaxial cylinders

Electromagnetically driven flows of electrolytes in an annulus bounded by cylindrical vertical electrodes and a solid bottom have been extensively studied experimentally and theoretically (e.g. Pérez-Barrera et al. 2016; Suslov et al. 2017; McCloughan & Suslov 2020). It was found that the steady azimuthal flow may become unstable giving rise to free-surface vortices developing close to the outer cylindrical wall. The steady flow field has a three-dimensional toroidal structure while the deformation of the upper free surface is negligible.

However, in thin liquid layers the film deformation can no longer be neglected as demonstrated in Wu et al. (1995) using a mechanically driven flow in an unsupported soap film spanning the gap between two thin coaxial discs. If the outer disc is fixed and the inner one is rotated, the fluid is set in motion in an azimuthal direction similar to a Couette cell flow. Centrifugal forces push the liquid towards the outer disc making the film thinner near the inner disc. Rather unexpectedly, the flow was found to be laminar and the onset of turbulence was not observed even at the linear rotation speed of up to $3\ \textrm {ms}^{-1}$.

Inspired by these experiments, we consider an electromagnetically driven flow in an unsupported free film between two conducting coaxial cylindrical electrodes with radii $R_1$ and $R_2>R_1$ and placed in a vertical uniform magnetic field ${\boldsymbol {B}}=(0,0,B)$ as schematically shown in figure 2. The potential difference between the inner and outer electrodes is $V$.

Figure 2. The top (a) and side (b) views of the radial cross-section of an annular free film of electrically conducting fluid spanning the gap between two coaxial cylindrical electrodes with radii $R_1$ and $R_2>R_1$. The film is placed in a vertical uniform magnetic field ${\boldsymbol {B}}=(0,0,B)$. Electric current flowing through the film between the two electrodes generates a Lorentz force that drives the flow azimuthally.

In what follows we scale the radial coordinate $r$ with $R_2-R_1$, the film thickness $h$ with its average value $\langle h\rangle$ and choose the flow velocity scale in such a way that $\textit {Ca}\,\textit {Re}=1$ in (2.20a–d), that is, $U=\sqrt {\gamma \langle h\rangle /(\rho (R_2-R_1)^2)}$. With $B$ used as the magnetic field scaling, the Hartmann number becomes $\textit {Ha}^2=B^2(R_2-R_1)^2Kc_{b}^{(0)}/\mu$, where $c_b^{(0)}$ is the average solute concentration in the bulk. We scale the electric potential with voltage $V$ applied between the electrodes and introduce a new dimensionless parameter $W=Kc_{b}^{(0)}BV/(\rho U^2)$ that characterises the strength of the electric component $Kc_{b}^{(0)}BV/(R_2-R_1)$ of the Lorentz force acting on a unit volume of fluid relative to the radial pressure gradient $\rho U^2/(R_2-R_1)$. Parameter $W$ is similar to the Lorentz force parameter $Q=u_{lor}/u_{visc}$ introduced in Piedra et al. (2018), where $u_{lor}=Kc_{b}^{(0)}BV(R_2-R_1)/\mu$ is the characteristic velocity determined from the balance between the Lorentz force and viscous dissipation and $u_{visc}=\mu /(\rho (R_2-R_1))$ is the viscous velocity scale. Thus, in the scaling used here the effective Lorentz force parameter is given by $Q=\textit {Re}\,W=Kc_{b}^{(0)}BV (R_2-R_1)/(\mu U)$. It quantifies the ratio of $u_{lor}$ and the characteristic flow velocity scale $U$. Note that since $\textit {Re}\,\textit {Ca}=1$, the Lorentz force parameter can also be expressed as $Q=W/\textit {Ca}$. Scaling back to the physical variables we obtain

(3.1)\begin{equation} Q=\dfrac{Kc_{b}^{(0)}BV (R_2-R_1)^2}{\mu} \sqrt{\frac{\rho}{\gamma\langle h\rangle}}.\end{equation}

All other dimensionless parameters $\textit {Ma}$, $\textit {Ha}$, $\textit {Ca}$, $\textit {Pe}$ and $\textit {Sc}$ are obtained from (2.20a–d) by setting $L=R_2-R_1$. The dimensionless inner and outer radii are given by $\alpha$ and $1+\alpha$, respectively, where $\alpha =R_1/(R_2-R_1)$. The concentration of a surfactant is scaled using the average value $c_s^{(0)}$. Using the same symbols for non-dimensionless fields, we convert the invariant form of (2.47) to polar coordinates $(r,\theta )$ and obtain

(3.2)\begin{align} &\partial_tu_r +u_r\partial_ru_r+\frac{u_\theta}{r}\partial_\theta u_r-\frac{u_\theta^2}{r}\nonumber\\ &\quad =g(h)\partial_rh+\partial_r\left(\frac{\partial_rh}{r} +\partial_r^2h+\frac{\partial_\theta^2h}{r^2}\right)+\textit{Ca}\left(\frac{\partial_ru_r}{r}+\partial_r^2u_r +\frac{\partial_\theta^2u_r}{r^2}-\frac{u_r}{r^2}-\frac{2\partial_\theta u_\theta}{r^2}\right)\nonumber\\ &\qquad -\textit{Ca}\,\textit{Ha}^2u_r -{\textit{Ca}\,\textit{Q}} \frac{\partial_\theta\phi}{r}+\frac{\textit{Ca}}{h}V_r+3\,\textit{Ca}\,\partial_r\left(\frac{u_r}{r}+\partial_r u_r +\frac{\partial_\theta u_\theta}{r} \right) -\frac{\textit{Ca}\,\textit{Ma}}{\textit{Pe}}\frac{\partial_rc_s}{h}, \end{align}

(3.3)\begin{align} &\partial_tu_\theta + u_r\partial_ru_\theta+\frac{u_\theta}{r}\partial_\theta u_\theta +\frac{u_\theta u_r}{r}\nonumber\\ &\quad =\frac{1}{r}g(h)\partial_\theta h {\,+\,}\frac{1}{r}\partial_\theta\left(\frac{\partial_r h}{r}{\,+\,}\partial_{r}^2h {\,+\,}\frac{\partial_\theta^2h}{r^2}\right) +\textit{Ca}\left(\frac{\partial_ru_\theta}{r}{\,+\,}\partial_{r}^2u_\theta {\,+\,}\frac{\partial_{\theta}^2u_\theta}{r^2}{\,-\,}\frac{u_\theta}{r^2} {\,+\,}\frac{2\partial_\theta u_r}{r^2}\right)\nonumber\\ &\qquad +{\textit{Ca}\,\textit{Q}}\partial_r \phi +\frac{\textit{Ca}}{h}V_\theta-\textit{Ca}\,\textit{Ha}^2u_\theta +\frac{3\,\textit{Ca}}{r}\partial_\theta\left(\frac{u_r}{r}+\partial_r u_r +\frac{\partial_\theta u_\theta}{r} \right) -\frac{\textit{Ca}\,\textit{Ma}}{\textit{Pe}}\frac{\partial_\theta c_s}{hr}, \end{align}

with

(3.4)\begin{align} V_r&=2\left(\partial_rh\partial_ru_r +\frac{1}{r^2}\partial_\theta h\partial_\theta u_r -\frac{1}{r^2}u_\theta\partial_\theta h\right) +\frac{1}{r^2}(\partial_r[ru_\theta] -\partial_\theta u_r)\partial_\theta h\nonumber\\ &\quad +\frac{2}{r}(\partial_r[ru_r]+\partial_\theta u_\theta)\partial_r h, \end{align}

(3.5)\begin{align} V_\theta&=2\left(\partial_rh\partial_ru_\theta +\frac{1}{r^2}\partial_\theta h\partial_\theta u_\theta +\frac{1}{r^2}u_r\partial_\theta h\right) -\frac{1}{r}(\partial_r[ru_\theta]-\partial_\theta u_r)\partial_r h\nonumber\\ &\quad +\frac{2}{r^2}(\partial_r[ru_r] +\partial_\theta u_\theta)\partial_\theta h. \end{align}

The dynamic equations for the salt and surfactant concentrations and the kinematic condition are given by

(3.6)$$\begin{gather} \partial_t[hc_b]+\frac{1}{r}(\partial_r[rhc_bu_r]+\partial_\theta[hc_bu_\theta]) =\frac{\textit{Sc}^{-1}\,\textit{Re}^{-1}}{r^2}[r\partial_r[rh\partial_rc_b]+\partial_\theta[h\partial_\theta c_b]], \end{gather}$$

(3.7)$$\begin{gather}\partial_t c_s+\frac{1}{r}(\partial_r[rc_su_r]+\partial_\theta[c_su_\theta]) =\frac{\textit{Pe}^{-1}}{r^2}[r\partial_r[r\partial_rc_b]+\partial_\theta^2c_s], \end{gather}$$

(3.8)$$\begin{gather}\partial_th+\frac{1}{r}(\partial_r[rhu_r]+\partial_\theta[hu_\theta])=0. \end{gather}$$

The system is completed by the continuity equation for the electric current

(3.9)\begin{equation} \partial_r[c_brh({\textit{Ca}\,\textit{Ha}^2} u_\theta-{\textit{Ca}\,\textit{Q}}\partial_r\phi)] -\partial_\theta\left[\frac{c_bh}{r}({\textit{Ca}\,\textit{Ha}^2} ru_r +{\textit{Ca}\,\textit{Q}}\partial_\theta\phi)\right]=0.\end{equation}

The system of equations (3.3)–(3.9) admits a steady solution that corresponds to the azimuthal flow field $u_r=0$, $u_\theta =f(r)$ induced by axisymmetric electric potential $\phi (r)$ in a film with axisymmetric profile $h(r)$ containing uniformly dissolved salt with constant bulk concentration $c_b=1$ and covered by a uniformly distributed surfactant with a surface concentration $c_s=1$. In what follows we study the properties and linear stability of the base azimuthal flow field, the instability of which determines the onset of the secondary possibly non-axisymmetric finite-amplitude flows.

The functions $f(r)$, $h(r)$ and $\phi (r)$ are found from

(3.10)$$\begin{gather} \left(\dfrac{(rh')'}{r}\right)'+g(h)h'+\dfrac{f^2}{r}=0, \end{gather}$$

(3.11)$$\begin{gather}f''+\dfrac{f'}{r}-\dfrac{f}{r^2}-\textit{Ha}^2\,f+{\textit{Q}}\phi' +\dfrac{h'}{h}\left(\,f'-\dfrac{f}{r}\right)=0, \end{gather}$$

(3.12)$$\begin{gather}(r h({\textit{Q}}\phi'-{\textit{Ha}^2}\,f))'=0, \end{gather}$$

where primes denote the radial derivative ${\textrm {d}}/{\textrm {d}r}$.

Equation (3.12) is integrated once to yield

(3.13)\begin{equation} \phi'={\frac{\textit{Ha}^2}{\textit{Q}}}f-\frac{e}{rh},\end{equation}

where constant $e$ is linked to the potential difference $\phi (1+\alpha )-\phi (\alpha )={1}$ between the electrodes via

(3.14)\begin{equation} {1=\frac{\textit{Ha}^2}{Q}}\int_\alpha^{1+\alpha}f(r)\,\textrm{d}r-e \int_\alpha^{1+\alpha}\frac{\textrm{d}r}{rh}.\end{equation}

The term $e/(rh)$ in (3.13) is related to the radial current density

(3.15)\begin{equation} j_r={\textit{Ca}\,\textit{Ha}^2}f-{\textit{Ca}\,\textit{Q}}\phi'=\frac{{\textit{Ca}\,\textit{Q}}e}{rh}. \end{equation}

The total steady current through the vertical cylindrical section of the film at any radial location $\alpha \leq r\leq 1+\alpha$ is independent of the radius of a cross-section and is given by $4{\rm \pi} rhj_r=4{\rm \pi} \,{\textit {Ca}\,\textit {Q}}e$.

Eliminating $\phi$ from (3.11), we obtain two coupled equations for $f$ and $h$,

(3.16)$$\begin{gather} \left(\dfrac{(rh')'}{r}\right)'+g(h)h'+\dfrac{f^2}{r}=0, \end{gather}$$

(3.17)$$\begin{gather}f''+\dfrac{f'}{r}-\dfrac{f}{r^2}-{\textit{Q}}\dfrac{e}{rh} +\dfrac{h'}{h}\left(\,f'-\dfrac{f}{r}\right)=0. \end{gather}$$

Fluid velocity vanishes at the surface of the electrodes leading to $f(\alpha )=f(1+\alpha )=0$. The boundary condition for the film deformation must be compatible with the long-wave approximation used here, which only takes into account relatively small film slopes $h'\ll 1$. In what follows we assume that $h'(\alpha )=h'(1+\alpha )=0$.

We are looking for a solution of the boundary value problems (3.16) and (3.17) that corresponds to a given average film half-thickness

(3.18)\begin{equation} \frac{2}{1+2\alpha}\int_{\alpha}^{1+\alpha }h(r)r\,\textrm{d}r=1 \end{equation}

and satisfies the additional integral condition (3.14) for any given value of the applied voltage $V$ that only appears in the definition of parameter $\textit {Q}$.

For reference, we derive the approximate analytic solution that corresponds to the flow in a flat undeformed film. By setting $h=1$ and neglecting the centrifugal acceleration $f^2/r$, we find from (3.17) and (3.14) that

(3.19)\begin{equation} f={\alpha e\textit{Q}} \left[C\left(\frac{\alpha}{r}-\frac{r}{\alpha}\right) +\frac{r}{2\alpha}\ln\frac{r}{\alpha}\right]\!,\end{equation}

where

(3.20)\begin{equation} \left.\begin{gathered} C=\dfrac{(1+\alpha)^2\ln{(1+\alpha^{-1})}}{2(1+2\alpha)},\quad e=\dfrac{{1}}{\alpha^2\,\textit{Ha}^2D-\ln(1+\alpha^{-1})},\\ D=C\ln\left(1+\alpha^{-1}\right)-\dfrac{1+2\alpha}{8\alpha^2}. \end{gathered}\right\} \end{equation}

To find non-trivial solutions of the boundary value problem (3.16), (3.17) with the integral condition (3.18), we use a numerical continuation package AUTO (Doedel et al. 1994; Krauskopf et al. 2014). The trivial solution $f=0$ and $h=1$ that exists for $\textit {Q}=0$ is used as a starting point for numerical continuation with $\textit {Q}$ being gradually increased.

In the absence of the disjoining pressure, that is, for $g(h)=0$, the boundary value problem (3.16), (3.17), (3.14), (3.18) has an important scaling property. Namely, it contains three dimensionless parameters, $\textit {Ha}$, $\alpha$ and the Lorentz force parameter $\textit {Q}$, but only $\textit {Q}$ depends explicitly on the dimensional layer thickness $2\langle h\rangle$. This implies that, for any fixed $\textit {Ha}$ and $\alpha$, there exists a universal branch of solutions parameterised by (3.1). A solution that corresponds to an arbitrary value of the average film half-thickness $\langle h\rangle$ and an arbitrary applied voltage $V$ is found on the universal branch for the corresponding value of $\textit {Q}$.

Taking into account the above scaling property we consider a free film with an arbitrary average half-thickness $\langle h\rangle$ spanning the gap between cylindrical electrodes with radii $R_1=1$ cm and $R_2=2$ cm ($\alpha =1$). As an example, we chose fluid properties and a magnetic field strength similar to those used in Pérez-Barrera et al. (2016) and Suslov et al. (2017): $Kc_b^{(0)}=\sigma =5\ (\textrm {Ohm}\ \textrm {m})^{-1}$, $\mu =0.001\ \textrm {kg}\ \textrm {m}\ \textrm {s}^{-1}$, $\rho =1000\ \textrm {kg}\ \textrm {m}^{-3}$, $B=0.05\ \textrm {T}$. Additionally, we use $\gamma =0.03\ \textrm {N}\ \textrm {m}^{-1}$ for the surface tension coefficient. These correspond to $\textit {Ha}^2\approx 1.3\times 10^{-3}$. As the solution measure, we take the maximum flow velocity $f_{max}$ and the minimum film thickness $h_{min}$ attained at the inner cylinder ($r=\alpha$). The numerically obtained maximum velocity $f_{max}$ is shown in figure 3(a) by the solid line while the value found from the flat-film approximation (3.19) is depicted by the dashed line. The minimum film thickness is shown in the log-log scale in figure 3(b) indicating that $h_{min}$ asymptotically approaches zero as a power law function ${\sim }{\textit {Q}}^{-2.4}$. This implies that the solution exists for any fixed value of ${\textit {Q}}$ no matter how large it is. However, the film thickness becomes vanishingly small at the inner electrode indicating that the film is likely to rapture there.

Figure 3. (a) Maximum fluid velocity in a free annular film as a function of the Lorentz force parameter $\textit {Q}$ for $\textit {Ha}^2=1.3\times 10^{-3}$ and $\alpha =1$. The dashed and solid lines correspond to the flat-film approximation (3.19) and the numerical solution, respectively. (b) Minimum film thickness $h_{min}$ at the inner cylinder as a function of the applied voltage. The dashed line depicts the power law function ${\sim }({\textit {Q}})^{-2.4}$. (c) Film thickness $h(r)$ for the values of $\Delta \phi$ at points $1$ and $2$ labelled in panel (a). (d) Velocity $f(r)$ for solutions at points $1$ and $2$ in panel ($a$) (solid lines) and corresponding to the flow in the flat-film approximation (3.19) (dashed lines).

We also emphasise that all results presented in this paper are obtained by neglecting the disjoining pressure. This introduces a natural limitation on their applicability for films that are thinner than approximately 100 nm. For example, if $\langle h\rangle =10\ \mathrm {\mu }\textrm {m}$ as in figures 5 and 6 in § 4, the smallest dimensionless film thickness $h_{min}=10^{-7}\ \textrm {m}/\langle h\rangle$ for which the presented results are expected to remain valid is $h_{min}\approx 10^{-2}$, that is, about 1 % of the average film thickness.

The film profile and the flow velocity at points $1$ and $2$ are shown in figures 3(c) and 3(d), respectively. The dashed line in figure 3(d) corresponds to the approximate solution (3.19).

4. Linear stability of the azimuthal flow

In this section we study the linear stability of the base azimuthal flow $(u_r,u_\theta )=(0,f(r))$ in a free film with the half-thickness $h_0(r)$ in the absence of the disjoining pressure ($\varPi (h)=0$). It is anticipated that the least stable perturbations are azimuthally invariant due to the stabilising effect of the surface tension. Indeed, any perturbation that varies azimuthally must be periodic in $\theta$ and, consequently, be proportional to $\textrm {e}^{\textrm {i} n\theta }$, $n=0,1,2,\ldots\ $. Therefore, the magnitude of the stabilising surface tension terms in (3.3) increases as $n^3$ and is the smallest for $n=0$.

Equations (3.3)–(3.9) are linearised about the base flow by writing

(4.1)\begin{equation} \left.\begin{gathered} u_r={\rm e}^{\lambda t}{\tilde{u}}_r(r),\quad u_\theta=f(r)+{\rm e}^{\lambda t}{\tilde{u}}_\theta(r), \quad h=h_0+{\rm e}^{\lambda t}{\tilde{h}},\\ c_b=1+{\rm e}^{\lambda t}{\tilde{c}}_b,\quad c_s=1+{\rm e}^{\lambda t}{\tilde{c}}_s,\quad \phi'={\dfrac{\textit{Ha}^2}{\textit{Q}}}f-\dfrac{e}{rh_0} +{\rm e}^{\lambda t}{\tilde{\phi}}'(r), \end{gathered}\right\}\end{equation}

where $\lambda$ is the perturbation growth rate, $h_0=h_0(r)$ is the steady film profile and the tilded variables represent small-amplitude perturbations, substituting these in the equations and neglecting the products of perturbations. After dropping the tildes we obtain

(4.2)$$\begin{gather} \lambda u_r =-\frac{2fu_\theta}{r} +\left(\frac{(rh')'}{r}\right)'+4\,\textit{Ca}\left(\frac{(ru_r)'}{r}\right)' -\textit{Ca}\,\textit{Ha}^2u_r\nonumber\\ \quad +\frac{2\,\textit{Ca}\, h_0'}{h_0}\left(\frac{u_r}{r}+2u_r'\right) -\frac{\textit{Ca}\,\textit{Ma}}{\textit{Pe} h_0} c'_s, \end{gather}$$

(4.3)$$\begin{gather} \lambda u_\theta=-u_rf'-\frac{fu_r}{r}+\textit{Ca}\left(\frac{(ru_\theta)'}{r}\right)' -{\textit{Ca}\,\textit{Ha}^2 u_\theta+\textit{Ca}\,\textit{Q}\phi'}\nonumber\\ \quad +\frac{\textit{Ca}\, h_0'}{h_0}\left(u_\theta'-\frac{u_\theta}{r}\right) +\textit{Ca}\left(\frac{h}{h_0}\right)'\left(\,f'-\frac{f}{r}\right)\!, \end{gather}$$

(4.4)$$\begin{gather} \lambda h=-\frac{1}{r}\left(rh_0u_r\right)', \end{gather}$$

(4.5)$$\begin{gather}\lambda c_bh_0+\lambda h=-\frac{1}{r}(rh_0u_r)' +\textit{Sc}^{-1}\,\textit{Re}^{-1}\frac{(rh_0(c_b)')'}{r}, \end{gather}$$

(4.6)$$\begin{gather}\lambda c_s=-\frac{1}{r}\left(ru_r\right)' +\textit{Pe}^{-1}\frac{(r(c_s)')'}{r}, \end{gather}$$

(4.7)$$\begin{gather}0=\left(rh_0\left( {\dfrac{\textit{Ha}^2}{\textit{Q}}} u_\theta-\phi'\right)\right)' +\left(\frac{e\left( h+c_b h_0\right)}{ h_0}\right)'. \end{gather}$$

The flow velocity vanishes at $r=\alpha$ and $r=1+\alpha$ so that $u_r=u_\theta =0$ there. This leads to the automatic conservation of the total volume of the fluid

(4.8)\begin{equation} \int_\alpha^{1+\alpha}2{\rm \pi} hr\,\textrm{d}r=-\frac{1}{\lambda}\int_\alpha^{1+\alpha} \frac{2{\rm \pi}}{r}\left(rh_0u_r\right)'r\,\textrm{d}r=0.\end{equation}

To describe moving contact lines at the surface of the electrodes, we assume that the dynamic contact angle is equal to its static value at all times, that is, we require that $h'(\alpha )=h'(1+\alpha )=h_0'(\alpha )=h_0'(1+\alpha )=0$. The case of the dynamically changing contact angle and non-zero wetting line friction will be considered in future studies. Differentiating (4.4) and applying the conditions and $u_r(\alpha )=u_\theta (\alpha )=u_r(1+\alpha )=u_\theta (1+\alpha )=0$ we obtain two additional boundary conditions for the radial velocity $u_r$,

(4.9)\begin{equation} u_r'(\alpha)+u_r''(\alpha) =\frac{u_r'(1+\alpha)}{1+\alpha}+u_r''(1+\alpha)=0.\end{equation}

Integrating the equation for the perturbation of the electric potential (4.7) once we obtain

(4.10)\begin{equation} {\dfrac{\textit{Ha}^2}{\textit{Q}}}u_\theta-\phi'=\frac{c}{rh_0}-\frac{eh}{rh_0^2} -\frac{ec_b}{rh_0},\end{equation}

where $c$ is some constant. Integrating (4.10) and imposing the condition $\phi (\alpha )=\phi (1+\alpha )=0$ we find that

(4.11)\begin{equation} {\dfrac{\textit{Ha}^2}{\textit{Q}}}\int_\alpha^{1+\alpha}u_\theta\,\textrm{d}r =c\int_\alpha^{1+\alpha}\frac{\textrm{d}r}{rh_0} -e\int_\alpha^{1+\alpha}\frac{h}{rh_0^2}\textrm{d}r -e\int_\alpha^{1+\alpha}\frac{c_b}{rh_0}\textrm{d}r.\end{equation}

Multiplying (4.2) and (4.3) by $\lambda$, using (4.4) and (4.10) to eliminate $h$ and $\phi '$ and, subsequently, differentiating (4.5) and (4.6) with respect to the radius $r$ we arrive at a nonlinear eigenvalue problem,

(4.12)\begin{align} \lambda^2 u_r-\frac{2\lambda fu_\theta}{r} &=-\left(\frac{(r(r^{-1}\left(rh_0u_r\right)')')'}{r}\right)' +4\lambda\,\textit{Ca}\left(\frac{(ru_r)'}{r}\right)' -\lambda \,\textit{Ca}\,\textit{Ha}^2u_r\nonumber\\ &\quad +\frac{2\,\textit{Ca}\,\lambda h_0'}{h_0}\left(\frac{u_r}{r}+2u_r'\right) -\frac{\textit{Ca}\,\textit{Ma}}{\textit{Pe}}\frac{\lambda c_s'}{h_0}, \end{align}

(4.13)\begin{align} \lambda^2 u_\theta+\lambda u_rf' &=-\frac{\lambda fu_r}{r} +\lambda\,\textit{Ca}\left(\frac{(ru_\theta)'}{r}\right)' -{\textit{Ca}\,\textit{Q}}\left(\frac{e (rh_0 u_r)'}{r^2h_0^2} -\frac{\lambda e c_b}{rh_0}+\frac{\lambda c}{rh_0}\right)\nonumber\\ &\quad +\frac{\lambda\,\textit{Ca}\, h_0'}{h_0} \left(u_\theta'-\frac{u_\theta}{r}\right) -\textit{Ca}\left(\frac{(rh_0u_r)'}{rh_0}\right)'\left(\,f'-\frac{f}{r}\right)\!, \end{align}

(4.14)\begin{align} \lambda c_b'&=\textit{Sc}^{-1}\,\textit{Re}^{-1}\left(\frac{(rh_0c_b')'}{rh_0}\right)',\end{align}

(4.15)\begin{align} \lambda c_s' &= \textit{Pe}^{-1}\left(\frac{(rc_s')'}{r}\right)' -\left(\frac{\left(ru_r\right)'}{r}\right)'\end{align}

that must be solved in conjunction with the integral condition (4.11). The set of boundary conditions (4.9) and $u_r(\alpha )=u_\theta (\alpha )=u_r(1+\alpha )=u_\theta (1+\alpha )=0$ must be extended with

(4.16)\begin{equation} c_s'(\alpha)=c_b'(\alpha)=c_s'(1+\alpha)=c_b'(1+\alpha)=0,\end{equation}

which accounts for the chemically passive impenetrable boundaries of the two electrodes. Note that unlike (3.16) and (3.17) the eigenvalue problem (4.15) contains the average film thickness $\langle h\rangle$ as a part of the capillary number $\textit {Ca}$.

4.1. Linear stability of a flat film with no applied voltage

In this section we consider the stability of a flat film in the absence of an electric current. With $h_0=1$, $f=0$ and $e=0$ the eigenvalue problem (4.12)–(4.15) and the integral condition (4.11) reduce to three decoupled eigenvalue problems: one for the azimuthal velocity perturbations $u_\theta$, one for the radial velocity $u_r$ and surfactant $c_s$ perturbations and one for the perturbation of the solute concentration $c_b$:

(4.17)$$\begin{gather} \lambda u_\theta =\textit{Ca}\,\mathcal{L}\{u_\theta\} -\frac{\textit{Ca}\,\textit{Ha}^2}{r\ln\left(1+\alpha^{-1}\right)} \int_\alpha^{1+\alpha}u_\theta\,\textrm{d}r, \end{gather}$$

(4.18)$$\begin{gather}\lambda^2 u_r =- \mathcal{L}\{\mathcal{L}\{u_r\}\}+4\lambda\textit{Ca}\,\mathcal{L}\{u_r\} -\lambda\textit{Ca}\,\textit{Ha}^2u_r-\textit{Ca}\,\textit{Ma}\,\textit{Pe}^{-1}\lambda c_s', \end{gather}$$

(4.19)$$\begin{gather}\lambda c_s'=\textit{Pe}^{-1}\,\mathcal{L}\{c_s'\} -\mathcal{L}\{u_r\}, \end{gather}$$

(4.20)$$\begin{gather}\lambda c_b'=\textit{Sc}^{-1}\,\textit{Re}^{-1}\mathcal{L}\{c_b'\}. \end{gather}$$

Here $\mathcal{L}\{u\}\equiv (r^{-1}(ru)')'$.

The eigenvalue problem (4.17)–(4.20) can be solved analytically in terms of the auxiliary eigenvalue problem for the operator $\mathcal {L}$,

(4.21)\begin{equation} \mathcal{L}\{u\}=-\varLambda u,\end{equation}

which coincides with Bessel's differential equation. The solution of (4.21) that satisfies the Dirichlet boundary conditions $u(\alpha )=u(1+\alpha )=0$ exists only for real positive $\varLambda$ and is given by

(4.22)\begin{equation} u(r)=C_1 {\rm J}_1\left(r\sqrt{\varLambda}\right) +C_2{\rm Y}_1\left(r\sqrt{\varLambda}\right)\!,\end{equation}

where $C_1$ and $C_2$ are arbitrary constants and $\textrm {J}_1$ and $\textrm {Y}_1$ are the Bessel functions of order one of the first and second kind, respectively. Applying the boundary conditions we obtain the solvability condition for constants $C_1$ and $C_2$ that determines the entire spectrum of discrete eigenvalues $\varLambda$,

(4.23)\begin{equation} {\rm J}_1\left(\alpha\sqrt{\varLambda}\right) {\rm Y}_1\left((1+\alpha)\sqrt{\varLambda }\right) -{\rm J}_1\left((1+\alpha)\sqrt{\varLambda}\right) {\rm Y}_1\left(\alpha\sqrt{\varLambda}\right)=0.\end{equation}

It follows from (4.21)–(4.23) that the spectrum of eigenvalues $\lambda _{c_b}$ of the bulk solute concentration perturbations (4.20) is real and negative, i.e.

(4.24)\begin{equation} \lambda_{c_b}=-(\textit{Sc}\,\textit{Re})^{-1}\varLambda,\end{equation}

and the corresponding eigenfunction is given by

(4.25)\begin{equation} c_b'(r)=C\left[ {\rm J}_1\left(r\sqrt{\varLambda}\right) {\rm Y}_1\left(\alpha\sqrt{\varLambda}\right) -{\rm Y}_1\left(r\sqrt{\varLambda}\right) {\rm J}_1\left(\alpha\sqrt{\varLambda}\right)\right]\!,\end{equation}

where $C$ is an arbitrary constant.

The eigenvalue problem (4.18) and (4.19) for $u_r$ and $c_s'$ can be solved in a similar way using the eigenfunctions of the operator $\mathcal {L}$. The solution that satisfies $u_r(\alpha )=u_r(1+\alpha )=0$ and $c_s'(\alpha )=c_s'(1+\alpha )=0$ is given by

(4.26)\begin{equation} \left.\begin{gathered} u_r(r) =C_1\left[ {\rm J}_1\left(r\sqrt{\varLambda}\right) {\rm Y}_1\left(\alpha\sqrt{\varLambda}\right) -{\rm Y}_1\left(r\sqrt{\varLambda}\right) {\rm J}_1\left(\alpha\sqrt{\varLambda}\right)\right]\!,\\ c_s'(r) =C_2u_r, \end{gathered}\right\}\end{equation}

where $C_1$ and $C_2$ are some constants.

Substituting (4.26) into (4.18) and (4.19) we obtain

(4.27)$$\begin{gather} \lambda^2=-\varLambda^2-\textit{Ca}(4\varLambda+\textit{Ha}^2)\lambda-C_2\,\textit{Ca}\,\textit{Ma}\,\textit{Pe}^{-1}\lambda, \end{gather}$$

(4.28)$$\begin{gather}\lambda C_2=\varLambda-\textit{Pe}^{-1}\varLambda C_2, \end{gather}$$

and then eliminating $C_2$ from (4.27) we arrive at a cubic equation for $\lambda$,

(4.29)\begin{equation} (\textit{Pe}\,\lambda+\varLambda)(\lambda^2 +\textit{Ca}(4\varLambda+\textit{Ha}^2)\lambda+\varLambda^2) +b\varLambda\lambda\,\textit{Pe}=0,\end{equation}

where $b=\textit {Ca}\,\textit {Ma}\,\textit {Pe}^{-1}>0$ characterises the strength of the Marangoni flow.

For any admissible value of $\varLambda$ from (4.23), one needs to solve (4.29) to find the eigenvalue $\lambda$. Then the corresponding eigenfunctions (4.26) only contain one arbitrary scaling factor $C_1$ with $C_2=\varLambda /(\lambda +\textit {Pe}^{-1}\varLambda )$. Here we consider two physically distinct situations: the diffusion-dominated regime, when the surface diffusivity is large, i.e. $d_s\to \infty$, and the advection-dominated regime, when $d_s\to 0$. Since the Hartmann number $\textit {Ha}$, the capillary number $\textit {Ca}$ and parameter $b=\textit {Ca}\,\textit {Ma}\,\textit {Pe}^{-1}$ in (4.29) do not depend on $d_s$, the diffusion-dominated regime corresponds to $\textit {Pe}\to 0$ with $\textit {Ha}$, $\textit {Ca}$ and $b$ remaining finite. In this case (4.29) has three distinct solutions:

(4.30)$$\begin{gather} \lambda_{1,2}=-\frac{\textit{Ca}\left(4\varLambda+\textit{Ha}^2\right)+b\,\textit{Pe}}{2} \pm\frac{\varOmega}{2}\left(1+b\,\textit{Pe}\frac{\textit{Ca}(4\varLambda+\textit{Ha}^2)} {2\varOmega^2}\right)+O(\textit{Pe}^2), \end{gather}$$

(4.31)$$\begin{gather}\lambda_3=-\textit{Pe}^{-1}\varLambda+b\,\textit{Pe}+O(\textit{Pe}^2). \end{gather}$$

Here $\varOmega =\sqrt {\textit {Ca}^2(4\varLambda +\textit {Ha}^2)^2-4\varLambda ^2}$.

Note that $\lambda _3$ is real and negative and its magnitude is always much larger than $|\lambda _{1,2}|$. Since $\varLambda$ is real and positive, we conclude that the real parts of $\lambda _{1,2}$ are always negative. Moreover, $\lambda _{1,2}$ become complex if $\textit {Ca}(4\varLambda +\textit {Ha}^2)<2\varLambda$ implying that the radial perturbation mode undergoes the transition from a monotonic to oscillatory decay. In physical variables, the condition for the oscillatory decay of the radial mode is

(4.32)\begin{equation} \sqrt{\rho\gamma\langle h\rangle}> 2\mu+\frac{B^2 (R_2-R_1)^2\sigma}{2\varLambda},\end{equation}

where the electric conductivity is $\sigma =Kc_b^{(0)}$ and $\varLambda$ depends on the ratio of the radii $R_2/R_1$ via parameter $\alpha$. It is instructive to compare condition (4.32) with the linear stability of an unbounded flat free layer in the absence of the magnetic field. Neglecting the disjoining pressure, the growth rate $\omega (k)$ of the least stable mode with the wavenumber $k$ in an unbounded horizontal free film can be obtained from (30) in Erneux & Davis (1993):

(4.33)\begin{equation} \frac{\mu}{\rho}\omega(k)=-2k^2 +k^2\sqrt{4-\frac{\rho\langle h\rangle\gamma}{\mu^2}}. \end{equation}

It follows from (4.33) that the critical thickness $2\langle h\rangle _c$ of the layer above which the relaxation dynamics is oscillatory is given by

(4.34)\begin{equation} 2\langle h\rangle_c=\frac{8\mu^2}{\rho\gamma}.\end{equation}

This coincides with our result (4.32) for $B=0$.

It is seen from (4.30) that in the absence of the Marangoni flow, that is, when $b=0$, the eigenvalue of the radial velocity perturbation with the largest real part is given by

(4.35)\begin{equation} \lambda_1=-\frac{\textit{Ca}\left(4\varLambda+\textit{Ha}^2\right)}{2} +\frac{\varOmega}{2}.\end{equation}

The perturbation of the surfactant is decoupled from that of the radial flow and has a negative real eigenvalue $\lambda _3=-\varLambda \,\textit {Pe}^{-1}$. In this regime, any perturbation of the surfactant distribution relaxes on the time scale $|\lambda _3|^{-1}$, which is much shorter than the characteristic decay time $-{\rm Re} ({\lambda _{1,2}}^{-1})$ of fluid motion. In the presence of the Marangoni flow when $b\ne 0$, the perturbations of the radial velocity and surfactant concentrations are coupled and their dynamics is characterised by the leading eigenvalues $\lambda _{1,2}$. The Marangoni flow leads to a further stabilisation of the leading perturbation mode as follows from (4.30). Indeed, by analysing the real parts of the leading eigenvalues we conclude that

(4.36)\begin{equation} {\rm Re}(\lambda_{1,2})|_{b>0}<{\rm Re}(\lambda_{1,2})|_{b=0}<0 \end{equation}

regardless of the sign of $\varOmega ^2$. As a consequence, the characteristic decay time of the flow perturbation decreases in the presence of the Marangoni effect.

As follows from (4.19), in the advection-dominated regime $\textit {Pe}\to \infty$ the dynamics of the surfactant perturbation is governed by the radial flow $u_r$. Indeed in this limit $\lambda c_s'=-\mathcal{L}\{u_r\}$, which shows that the surfactant plays the role of an active scalar field advected by the flow while its gradient influences the stability of the flow. By letting $\textit {Pe}\to \infty$ in (4.28) and then substituting $C_2=\varLambda /\lambda$ in (4.27) we obtain

(4.37)\begin{equation} \lambda_{{\pm}}\approx\tfrac{1}{2}\left[-\textit{Ca}\left(4\varLambda+\textit{Ha}^2\right) \pm\sqrt{\textit{Ca}^2\left(4\varLambda+\textit{Ha}^2\right)^2 -4\varLambda(\varLambda+b)}\right].\end{equation}

From (4.37) we see that the Marangoni flow has no effect on the stability of the base flow if the expression under the radical is negative. However, if

(4.38)\begin{equation} \textit{Ca}^2\left(4\varLambda+\textit{Ha}^2\right)^2-4\varLambda(\varLambda+b)>0, \end{equation}

the leading eigenvalue $\lambda _+$ becomes real and negative, and the presence of surfactant has a stabilising effect since $|\lambda _+|_{b>0}>|\lambda _+|_{b=0}$. These analytical results extend an earlier study on the linear stability of planar soap films (Miksis & Ida 1998) by including the Lorentz force effects. The observation of the stabilising role of the Marangoni flow in the limit of diffusion-dominated and advection-dominated regimes is in agreement with Miksis & Ida (1998), where it was also found that for long-wavelength perturbations the presence of the Marangoni flow decreases the growth rate of the dominant perturbation mode.

To illustrate the structure of the oscillatory radial mode, we consider the diffusion-dominated regime in a film with the average thickness $2\langle h\rangle =20\ \mathrm {\mu }\textrm {m}$ and take all other parameters as in figure 3. For $\alpha =1$, the leading eigenvalue of the operator $\mathcal {L}$ is $\varLambda \approx 10.218$, which corresponds to the complex leading eigenvalue of the radial mode $\lambda _r\approx -1.179\pm 10.149\textrm {i}$. The corresponding eigenfunction $u_r$ is shown in figure 4(a). Figure 4(b) depicts the instantaneous streamlines of the corresponding flow field in a vertical cross-section of the film $(r,z)$. The streamlines are obtained by recalling that the vertical flow velocity $w$ is given by $w(r,z)=-r^{-1}(ru_r)'z$ so that the kinematic equation (4.4) can be written in the form $\partial _t h =-w(r,1)=- r^{-1}(ru_r)'$. The film interface oscillates about $h_0=1$ with a decreasing amplitude while the fluid flows from the inner to the outer cylinder and back.

Figure 4. (a) Leading eigenfunction $u_r=\textrm {Y}_1(\alpha \sqrt {\varLambda }) \textrm {J}_1(r\sqrt {\varLambda }) -\textrm {J}_1(\alpha \sqrt {\varLambda }) \textrm {Y}_1(r\sqrt {\varLambda })$ of the radial perturbation mode for the same parameters as in figure 3 and $\langle h\rangle =10 \ \mathrm {\mu }\textrm {m}$. (b) Streamlines of the radially perturbed flow field in a vertical cross-section of the film.

Figure 5. (a) Real part of the first three leading eigenvalues as a function of the value of $\textit {Q}$ for the same parameters as in figure 3. The solid (dashed) lines correspond to complex (purely real) eigenvalues, respectively. Labels BP and NS mark the loci of the branching point of the azimuthal velocity mode and the point of neutral stability of the radial velocity mode, respectively; (b) the relative strength of the radial to azimuthal velocity mode $\chi$; (c) the neutrally stable film profile at point NS in panel (a); (d) the azimuthal velocity $f_0$ in a neutrally stable film; the magnitudes of the neutrally stable radial (e) and azimuthal (f) velocity perturbations.

It is instructive to consider the limit of a vanishingly small inner radius, that is, $\alpha \to 0$. Using the asymptotic expressions for the Bessel functions, $\textrm {J}_1(x)\approx x/2$ and $\textrm {Y}_1(x)\approx -2/({\rm \pi} x)$, as $x\to 0$, it can be shown that the leading eigenvalue $\varLambda$ from (4.23) is finite and is given by the first non-zero root of $\textrm {J}_1(\sqrt {\varLambda })=0$, that is, $\varLambda =3.8317^2=14.6819$. For $\langle h\rangle =10\ \mathrm {\mu }\textrm {m}$, this corresponds to a complex eigenvalue of the radial mode $\lambda _r=-1.695\pm {\rm i} 14.584$. The eigenfunction $u_r$ from (4.26) has a removable singularity at $r\to \alpha \to 0$ and its shape is similar to that of $u_r$ shown in figure 4(a). Therefore, in the absence of the applied voltage, the leading radially symmetric oscillation mode in a circular unsupported free film is a damped rocking mode with the shape as in figure 4(b).

The eigenvalue problem (4.17) for the azimuthal velocity perturbation $u_\theta$ can only be found analytically for a weak magnetic field at $\textit {Ha}\to 0$. When $\textit {Ha}=0$, the spectrum of the azimuthal velocity perturbations is real and is given by

(4.39)\begin{equation} \lambda_{u_\theta}=-\varLambda\,\textit{Ca}.\end{equation}

Comparing (4.39) with (4.30) we observe that in the absence of the Marangoni flow ($b=0$) and when $\textit {Ha}=0$, the absolute value of the eigenvalue $|\lambda _{u_\theta }|$ of the monotonically stable azimuthal velocity perturbation is exactly half of the real part of the eigenvalue $\lambda _{u_r}$ of the radial velocity mode.

4.2. Linear stability of a deformed film in the presence of electric current

In this section we study the linear stability of the azimuthal flow in a deformed film in the diffusion-dominated regime, when perturbations of the surfactant and solute fields relax instantaneously. The azimuthal and radial velocity perturbation modes discussed in the previous section become coupled in the presence of an electric current. This implies that, for any infinitesimal value of $\textit {Q}$, the spectrum of the generalized eigenvalue problem (4.15) is discrete and contains the eigenvalues that originate from each of the possible radial and azimuthal velocity modes existing in the absence of current.

To visualise how the stability of the azimuthal flow changes with the applied voltage, we choose $\langle h\rangle =10\ \mathrm {\mu }\textrm {m}$ and keep all other parameters as in figure 3. The numerical continuation method is then employed to track each mode and the corresponding eigenvalue using the value of $\textit {Q}$ as the continuation parameter. To this end, the generalized eigenvalue problem (4.15) is solved simultaneously with (3.16) and (3.17). To quantify the relative coupling strength between the perturbations of the radial and the azimuthal velocity, we introduce the parameter

(4.40)\begin{equation} \chi=\arctan{\left(\frac{\displaystyle\int\nolimits_\alpha^{1+\alpha}|u_r|^2\,\textrm{d}r} {\displaystyle\int\nolimits_\alpha^{1+\alpha}|u_\theta|^2\,\textrm{d}r}\right)}.\end{equation}

Thus, $\chi ={\rm \pi} /2$ corresponds to the pure radial and $\chi =0$ to pure azimuthal modes, respectively.

The real parts of the first three leading eigenvalues labelled by $r_1$, $\theta _1$ and $\theta _2$ are shown in figure 5(a). At $\textit {Q}=0$ the leading mode is the azimuthal velocity mode $\theta _1$ with the real eigenvalue $\lambda _{\theta _1}\approx -0.589$. The second least stable mode $r_1$ corresponds to the radial velocity. It has the complex eigenvalues $\lambda _{r_1}=-1.179\pm 10.149\textrm {i}$. The third mode $\theta _2$ is again the azimuthal velocity mode with the real eigenvalue $\lambda _{\theta _2}\approx -2.298$. As the value of $\textit {Q}$ increases, the two leading azimuthal velocity modes remain monotonically stable until the branching point BP is reached, where the two modes form a complex conjugate pair with a negative real part collide. A further increase of the value of $\textit {Q}$ leads to the destabilisation of the leading radial mode $r_1$, which becomes neutrally stable at the point NS, where $\textrm {Im}\{\lambda _{r_1}\}\not =0$. The corresponding film thickness profile $h_0(r)$ and the base azimuthal flow $f_0(r)$ are shown in figure 5(c,d), respectively.

Oscillatory neutrally stable perturbation is a mixture of radial and azimuthal flows as quantified by $\chi$ in figure 5(b). Since the perturbation fields $u_r$ and $u_\theta$ are both complex, the real physical radial and azimuthal perturbations of the base flow are given by the real and imaginary parts of $|u_r|\exp ({\textrm {i}(\textrm {Im}\{\lambda _{r_1}\}t+\varPsi _r(r)}))$ and $|u_\theta |\exp ({\textrm {i}(\textrm {Im}\{\lambda _{r_1}\}t +\varPsi _\theta (r))})$ with spatially varying phase shifts $\varPsi _r=\arctan (\textrm {Im}\{u_r\}/\textrm {Re}\{u_r\})$ and $\varPsi _\theta =\arctan (\textrm {Im}\{u_\theta \}/ \textrm {Re}\{u_\theta \})$. The spatially varying amplitudes of the neutrally stable radial and azimuthal velocity perturbations $|u_r|$ and $|u_\theta |$ are shown in figure 5(e,f).

To gain deeper understanding of how the stability of the base flow changes with other parameters in figure 6(a), we show the neutral stability curve for $\textit {Ha}^2=1.3\times 10^{-3}$ in the plane $(\textit {Q}_c,\textit {Ca})$, where $\textit {Q}_c$ is the critical value of the Lorentz force parameter above which the base flow is linearly unstable. It is noteworthy that there exists a finite limiting value of $\textit {Q}_c=124$ as $\textit {Ca}\to 0$. Such a limiting behaviour of the neutral stability curves confirms the dynamic nature of the flow instability. Indeed, for the fixed $\langle h\rangle$, viscosity $\mu$ and density $\rho$, the limit of $\textit {Ca}\rightarrow 0$ corresponds to a large surface tension $\gamma \to \infty$. The existence of a finite value of $\textit {Q}_c$ implies that regardless of the strength of stabilising surface tension forces the instability can always be induced if the applied voltage exceeds the critical value $V_c$.

Figure 6. (a) Neutral stability curve in the $(\textit {Q}_c,\textit {Ca})$ plane for $\textit {Ha}_1^2=0.0013$. (b) Neutral stability curve in the $(\textit {Q}_c,\textit {Ha}^2)$ plane for $\textit {Ca}=10^{-5}$. The vertical dashed line corresponds to $\textit {Q}_c=124$.

We set $\textit {Ca}=10^{-5}$ and trace the locus of the neutral stability in the $(\textit {Q}_c,\textit {Ha}^2)$ plane in figure 6(b). The dashed line corresponds to $\textit {Q}_c=124$ and it fits almost perfectly the lower part of the curve (small $\textit {Ha}^2$). This simple relationship between $\textit {Ha}^2$ and $\textit {Q}_c$ represents a universal stability threshold in the limit of small capillary and Hartmann numbers. Reintroducing dimensional variables from (3.1) we obtain the critical value of the applied voltage $V_c$,

(4.41)\begin{equation} V_c=\frac{124\mu}{B\sigma (R_2-R_1)^2} \sqrt{\frac{\gamma\langle h\rangle}{\rho}}.\end{equation}

The asymptotic result (4.41) is valid for the selected radii ratio $R_2/R_1=2$ and $(\textit {Ca},\textit {Ha}^2)\to (0,0)$. At the critical value of $V_c$ the film is strongly deformed and has a shape similar to solution (2) in figure 3(c). The minimum value of the film thickness is attained at the inner cylinder and is approximately 6 % of $\langle h\rangle$.

5. Conclusions

We derived a set of leading-order equations in the lubrication approximation that describe the electromagnetically driven flow of electrolyte solutions and/or non-magnetic liquid metals in a thin horizontal free layer with deformable surfaces placed in a uniform magnetic field normal to the layer. The equations are written in a generic coordinate-invariant form and can be used to study electromagnetically driven flows in an arbitrary geometry dictated by the shape and size of the deployed electrodes. The equations account for the presence of surfactants and chemical species dissolved in the bulk of the fluid. Inspired by recent studies of the electromagnetically driven flows in supported shallow annular layers between two coaxial cylinders (Figueroa et al. 2009; Pérez-Barrera et al. 2016; Suslov et al. 2017; McCloughan & Suslov 2020), we choose a similar geometry and apply the derived model to investigate the flow and its stability in an annular free film spanning the gap between two coaxial cylindrical electrodes.

Similar to mechanically driven flows in soap films (Wu et al. 1995), a steady azimuthal electromagnetically driven flow can only exist in a deformed layer, where the radial component of the gradient of the Laplace pressure balances the centrifugal force. This is in contrast to supported thicker layers, where the free-surface deformation is typically negligible compared with the thickness of the layer while the flow speed does not exceed several centimetres per second. The other important feature distinguishing the flows in free layers and films from those in supported layers is that in the former the Laplace pressure dominates while in the latter the hydrostatic pressure gradient defines the fluid trajectory in the plane of the layer.

If the intermolecular forces are neglected, the azimuthally invariant steady-state flow can be found for an arbitrarily large electric current flowing through the film. The minimal film thickness is achieved at the inner electrode. It decreases as a power law function of the applied voltage remaining non-zero so that the point of a true film rupture is never reached.

We determined that the azimuthal flow in approximately flat free films with a small velocity is linearly unconditionally stable. For relatively weak magnetic fields of the order of $10^{-2}$ T and fluid parameters corresponding to a weak electrolyte solution used in the experiments of Figueroa et al. (2009) and Pérez-Barrera et al. (2016), we found that the azimuthal velocity perturbations decay monotonically while the decay of radial velocity perturbations of the base flow in layers with the average thickness in the micrometre range is oscillatory. However, as the film thickness is decreased below a certain critical value given by condition (4.32) ($\lesssim$100 nm for a film existing between coaxial cylinders with the inner and outer radii of 1 and 2 cm, respectively), the relaxation dynamics is found to be dominated by viscous damping with a monotonic decay of a radial flow and the associated surface deformation. This result contrasts the observations of instabilities in supported thicker annular layers, where the primary flow becomes unstable with respect to three-dimensional perturbations of the velocity without a noticeable variation of the layer depth. The fluctuations of the solute concentration in the bulk has no effect on the growth rate of the leading modes. In the presence of a surfactant, the Marangoni effect leads to further stabilisation of the base flow, which is in agreement with earlier studies of planar soap films in the absence of magnetic fields (Miksis & Ida 1998).

By following the branch of steady-state solutions into the regime of large applied voltage and, consequently, large electric currents, we find that the steady azimuthal flow eventually becomes unstable with respect to a mixture of oscillatory azimuthal and radial velocity perturbations at a certain critical value of the applied voltage, at which the deformation amplitude of the layer is of the order of the average film thickness. This suggests that electromagnetically driven flows in free films may not be ideal candidates for studying two-dimensional turbulence since the primary instability of the base flow sets in only when the film is already strongly deformed. We note that a similar conclusion was made earlier in Rivera & Wu (2000), where it was hypothesised that strong damping caused by the interactions of the flow within a film with a surrounding gas layer that are enhanced by the surface deformation may be the cause for the energy leakage responsible for stronger than expected decays of the velocity correlation function. However, the two-dimensional turbulence is still possible if strongly non-uniform magnetic fields are used. Thus, we anticipate that the gradient of the magnetic field will further destabilise the base flow, lead to the generation of vorticity and, as a result, to a much more irregular flow pattern (Cuevas, Smolentsev & Abdou 2006).

Finally, we briefly mention the action of intermolecular forces characterised by the disjoining pressure. They play a major role in the instability and subsequent stabilisation of free soap films that are thinner than $\sim$100 nm. It is well known (Israelachvili 2011; Overbeek 1960) that long-range van der Waals forces destabilise free layers sandwiched between dielectric media with identical properties. These forces alongside the gravity-induced drainage of the fluid constitute the primary source of film instability. As the film thickness decreases below 10–50 nm, an electric double layer is typically formed consisting of the monolayers of soap ions adsorbed at each interface. Strong electric double-layer forces lead to the repulsion between the film surfaces and the formation of highly stable black soap films with a thickness under 50 nm. Therefore, it is important to study the role of the disjoining pressure on the steady azimuthal flow and its stability in the strong-current regimes when the deformation of the layer is significant. Intermolecular forces, black soap films and film rupture will become the topic of our future investigations.