Article contents
Electric field mediated von Kármán vortices in stratified microflows: transition from linear instabilities to coherent mixing
Published online by Cambridge University Press: 18 February 2019
Abstract
Application of an electric field across the pressure-driven stratified flow of a pair of miscible fluids inside a microchannel manifests interesting electrohydrodynamic (EHD) instabilities. Experiments uncover distinctive instability regimes with an increase in electric field Rayleigh number (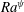 $Ra^{\unicode[STIX]{x1D713}}$) – a linear-onset regime, a time-periodic nonlinear regime analogous to the von Kármán vortex street in the downstream and a regime with coherent flow patterns. The experiments also reveal that such linear and nonlinear instabilities can be stimulated non-invasively in a microchannel to mix or de-mix fluids simply by turning the electric field on or off, indicating the suitability of the process for on-demand micromixing. The characteristics of these instabilities have been theoretically investigated with the help of an Orr–Sommerfeld framework, which discloses the possibility of five distinctive finite-wavenumber modes for the instability. The EHD stresses originating due to the application of electric field stimulate a pair of shorter-wavelength electric field modes beyond a critical value of
$Ra^{\unicode[STIX]{x1D713}}$) – a linear-onset regime, a time-periodic nonlinear regime analogous to the von Kármán vortex street in the downstream and a regime with coherent flow patterns. The experiments also reveal that such linear and nonlinear instabilities can be stimulated non-invasively in a microchannel to mix or de-mix fluids simply by turning the electric field on or off, indicating the suitability of the process for on-demand micromixing. The characteristics of these instabilities have been theoretically investigated with the help of an Orr–Sommerfeld framework, which discloses the possibility of five distinctive finite-wavenumber modes for the instability. The EHD stresses originating due to the application of electric field stimulate a pair of shorter-wavelength electric field modes beyond a critical value of 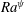 $Ra^{\unicode[STIX]{x1D713}}$. Increase in the levels of charge injection and EHD stresses lower the critical
$Ra^{\unicode[STIX]{x1D713}}$. Increase in the levels of charge injection and EHD stresses lower the critical 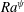 $Ra^{\unicode[STIX]{x1D713}}$ of these modes. The relatively longer-wavelength viscous mode is found to appear when the viscosity stratification between the fluid layers is high. Beyond a threshold Schmidt number (
$Ra^{\unicode[STIX]{x1D713}}$ of these modes. The relatively longer-wavelength viscous mode is found to appear when the viscosity stratification between the fluid layers is high. Beyond a threshold Schmidt number (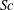 $Sc$), a diffusive mode is also found to appear near the mixed interfacial region. A thinner interface between the fluids at a higher
$Sc$), a diffusive mode is also found to appear near the mixed interfacial region. A thinner interface between the fluids at a higher 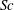 $Sc$ helps this mode to behave as the interfacial mode of immiscible fluids. Contrast of ionic mobility in the fluids leads to the appearance of the K-mode of instability at much shorter wavelengths. The reported phenomena can be of significance in the domains of microscale mixing, pumping, heat exchange, mass transfer and reaction engineering.
$Sc$ helps this mode to behave as the interfacial mode of immiscible fluids. Contrast of ionic mobility in the fluids leads to the appearance of the K-mode of instability at much shorter wavelengths. The reported phenomena can be of significance in the domains of microscale mixing, pumping, heat exchange, mass transfer and reaction engineering.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Dutta et al. supplementary material 1
Experimental video depicting linear regime I of instability developed in a benzenesilicone oil stratified flow through a 420 μm diameter channel, upon application of 0 – 300 V DC voltage through 420 μm diameter copper wire electrodes. The arrow indicates the direction of flow.
Dutta et al. supplementary material 2
Experimental video depicting non-linear regime II of instability developed in a benzene-silicone oil stratified flow through a 420 μm diameter channel, upon application of 300 – 600 V DC voltage through 420 μm diameter copper wire electrodes. The arrow indicates the direction of flow.
Dutta et al. supplementary material 3
Experimental video depicting non-linear regime III of instability developed in a benzene-silicone oil stratified flow through a 420 μm diameter channel, upon application of 600 – 900 V DC voltage through 420 μm diameter copper wire electrodes. The arrow indicates the direction of flow.
Dutta et al. supplementary material 4
Experimental video depicting non-linear chaotic regime IV of instability developed in a benzene-silicone oil stratified flow through a 420 μm diameter channel, upon application of 900 – 1000 V DC voltage through 420 μm diameter copper wire electrodes. The arrow indicates the direction of flow.
Dutta et al. supplementary material 5
Experimental video depicting response of benzene-silicone oil stratified flow through a 420 μm diameter channel, upon application of 0 – 500 V DC voltage through multiple copper wire electrodes of 420 μm diameter. The arrow indicates the direction of flow.
Dutta et al. supplementary material 6
CFD simulation video (corresponding to figure 19) depicting response of benzenesilicone oil stratified flow through a 420 μm diameter channel, upon application of 300 V DC voltage through copper wire electrodes of 420 μm diameter. The arrow indicates the direction of flow.
Dutta et al. supplementary material 7
CFD simulation depicting response of benzene-oleic acid stratified flow through a 420 μm diameter channel, upon application of 300 V DC voltage through copper wire electrodes of 420 μm diameter. The arrow indicates the direction of flow. The parameters used for the simulation are Sc = 500, KL=-4, EL=-0.15, and Re = 0.5.
Dutton et al. supplementary movie 8
CFD simulation depicting response of benzene-silicone oil stratified flow through a 420 μm diameter channel, upon application of 500 V DC voltage through copper wire electrodes of 420 μm diameter. The arrow indicates the direction of flow. The parameters used for the simulation are Sc = 500, KL=-0, EL=-0.15, and Re = 0.5.
- 18
- Cited by


