The elastocapillary Landau–Levich problem

Abstract

We study the classical Landau–Levich dip-coating problem for the case in which the interface possesses both elasticity and surface tension. The aim of the study is to develop a complete asymptotic theory of the elastocapillary Landau–Levich problem in the limit of small flow speeds. As such, the paper also extends our previous study on purely elastic Landau–Levich flow (Dixit & Homsy J. Fluid Mech., vol. 732, 2013, pp. 5–28) to include the effect of surface tension. The elasticity of the interface is described by the Helfrich model and surface tension is modelled in the usual way. We define an elastocapillary number, $\epsilon $, which represents the relative strength of elasticity to surface tension. Based on the size of $\epsilon $, we can define three different regimes of interest. In each of these regimes, we carry out asymptotic expansions in the small capillary (or elasticity) numbers, which represents the balance of viscous forces to surface tension (or elasticity).

In the weak elasticity regime, the film thickness is a small correction to the classical Landau–Levich law and can be written as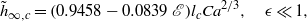

$$\begin{eqnarray*}{\tilde {h} }_{\infty , c} = (0. 9458- 0. 0839~\mathscr{E}){l}_{c} C{a}^{2/ 3} , \quad \epsilon \ll 1,\end{eqnarray*}$$

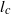where ${l}_{c} $ is the capillary length, 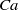$Ca$ is the capillary number and 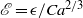$\mathscr{E}= \epsilon / C{a}^{2/ 3} $. In the elastocapillary regime, the film thickness is a function of $\epsilon $ through the power-law relationship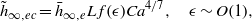

$$\begin{eqnarray*}{\tilde {h} }_{\infty , ec} = {\bar {h} }_{\infty , e} L\hspace{0.167em} f(\epsilon )C{a}^{4/ 7} , \quad \epsilon \sim O(1),\end{eqnarray*}$$

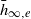where ${\bar {h} }_{\infty , e} $ is a numerical coefficient obtained in our previous study, 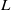$L$ is the elastocapillary length, and 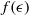$f(\epsilon )$ represents the functional dependence of film thickness on the elastocapillary parameter.