Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T19:28:36.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of three-dimensionality on instability and turbulence in a frontal zone

Published online by Cambridge University Press:  04 November 2015

Eric Arobone  and
Sutanu Sarkar
Eric Arobone
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
Sutanu Sarkar*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

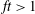Linear stability analysis and direct numerical simulation are used to investigate the evolution of a symmetrically unstable uniform frontal zone. Simulations in a three-dimensional computational domain capable of resolving near-symmetric currents develop strong nonlinearities without the emergence of pure symmetric instability. Linear stability analysis demonstrates that for $ft>1$ ( 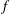$f$ is the Coriolis parameter and $t$ denotes time) the flow generates strongly asymmetric structures which become nearly symmetric when 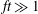$ft\gg 1$. Unlike the currents generated during pure symmetric instability, near-symmetric instability generates currents that do not align with isopycnals. This greatly modifies their energetics and evolution, leading to regions of the flow that are unstable to gravitational instability and energized by the reservoir of available potential energy. A high-resolution simulation demonstrates the flow evolution from near-symmetric currents to secondary shear-convective instabilities and finally, through tertiary instabilities, to fully three-dimensional turbulence. The effect of this sequence of instabilities is quantified through velocity and vorticity statistics as well as budgets for turbulent kinetic and potential energy. It is not until 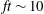$ft\sim 10$ that the energy source for fluctuations is primarily shear, in contrast to the purely symmetric instability which draws its energy exclusively from shear production.

JFM classification

Geophysical and Geological Flows: Ocean processes Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 252 - 273
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

D’Asaro, E., Lee, C., Rainville, L., Harcourt, R. & Thomas, L. 2011 Enhanced turbulence and energy dissipation at ocean fronts. Science 332 (6027), 318–322.CrossRefGoogle ScholarPubMed
Eady, E. T. 1949 Long waves and cyclone waves. Tellus 1, 33–52.Google Scholar
Griffiths, S. D. 2003a The nonlinear evolution of zonally symmetric equatorial inertial instability. J. Fluid Mech. 474, 245–273.Google Scholar
Griffiths, S. D. 2003b Nonlinear vertical scale selection in equatorial inertial instability. J. Atmos. Sci. 60, 977–990.Google Scholar
Hoskins, B. 1974 The role of potential vorticity in symmetric stability and instability. Q. J. R. Meteorol. Soc. 100, 480–482.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jones, S. & Thorpe, A. 1992 The three-dimensional nature of ‘symmetric’ instability. Q. J. R. Meteorol. Soc. 118, 227–258.Google Scholar
Lott, F., Plougonven, R. & Vanneste, J. 2012 Gravity waves generated by sheared three-dimensional potential vorticity anomalies. J. Atmos. Sci. 69, 2134–2151.CrossRefGoogle Scholar
Mamatsashvili, G., Vsarlosov, V., Hagelishvili, G., Hanishvili, R. & Kalashnik, M. 2010 Transient dynamics of nonsymmetric perturbations versus symmetric instability in baroclinic zonal shear flows. J. Atmos. Sci. 97, 2972–2989.Google Scholar
Moffatt, H. K. 1967 The interaction of turbulence with strong wind shear. In Proceedings of the 1965 URSI–IUGG International Colloquium on Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 139–154. Nauka.Google Scholar
Molemaker, M., McWilliams, J. & Capet, X. 2010 Balanced and unbalanced routes to dissipation in an equilibrated Eady flow. J. Fluid Mech. 654, 35–63.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Pieri, A., Godeferd, F., Cambon, C. & Salhi, A. 2013 Non-geostrophic instabilities of an equilibrium baroclinic state. J. Fluid Mech. 734, 535–566.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence, NASA Tech. Rep. 81315.Google Scholar
Salhi, A. & Pieri, A. B. 2014 Wave–vortex mode coupling in neutrally stable baroclinic flows. Phys. Rev. E 90, 1–15.CrossRefGoogle ScholarPubMed
Stone, P. 1966 On non-geostrophic baroclinic stability. J. Atmos. Sci. 23, 390–400.Google Scholar
Stone, P. 1970 On non-geostrophic baroclinic stability: part ii. J. Atmos. Sci. 27, 721–726.2.0.CO;2>CrossRefGoogle Scholar
Taylor, J. & Ferrari, R. 2009 On the equilibrium of a symmetrically unstable front via a secondary shear instability. J. Fluid Mech. 622, 103–113.CrossRefGoogle Scholar
Thomas, L., Taylor, J., Ferrari, R. & Joyce, T. 2013 Symmetric instability in the Gulf Stream. Deep-Sea Res. II 91, 96–110.Google Scholar
Thorpe, A. & Rotunno, R. 1989 Nonlinear aspects of symmetric instability. J. Atmos. Sci. 46, 1285–1299.Google Scholar