Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T01:55:01.346Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of thermophoresis on high-pressure binary-species boundary layers with uniform and non-uniform compositions

Published online by Cambridge University Press:  01 December 2022

Takahiko Toki Open the ORCID record for Takahiko Toki [Opens in a new window]  and
Josette Bellan Open the ORCID record for Josette Bellan [Opens in a new window]
Takahiko Toki
Affiliation:
California Institute of Technology, Pasadena, CA 91125, USA
Josette Bellan*
Affiliation:
California Institute of Technology, Pasadena, CA 91125, USA Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

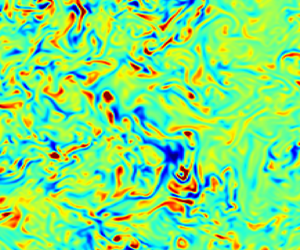
Direct numerical simulations of high-pressure binary-species temporal boundary layers are performed to investigate the flow physics for three situations: (1) uniform and equal composition, (2) uniform but unequal compositions and (3) non-uniform composition. Both colder- and hotter-wall situations compared with the free stream are simulated. The working fluid is a nitrogen/methane mixture. The analysis is performed at a case-specific self-similar state. Even when the initial composition is uniform, the methane mean mass fraction decreases near the colder wall, whereas it increases near the hotter wall and the mass fraction fluctuates in the entire boundary layer. Analysis of the species-mass diffusion balance and flow structures reveal that both mass-fraction variation and fluctuations are induced by the Soret effect. When the initial composition is non-uniform and the wall is colder, the methane mean mass fraction monotonically increases from the wall akin to its initial profile. However, when the wall is hotter the mean mass fraction decreases near the wall in contrast to its initial profile, a fact traced through the species-mass diffusion balance to the Soret effect being large and enriching methane near the wall. In contrast, the direction of the Soret flux is opposite for the colder wall, thus keeping the methane concentration small. Although the initial magnitude of the difference between the wall and free-stream temperature is the same in all cases, the situation is not symmetric between colder- and hotter-wall cases; the flow structure exhibits much smaller scales when the wall is hotter than when the wall is colder.

JFM classification

Boundary Layers: Boundary layer structure Mass Transport: Coupled diffusion and flow Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 952 , 10 December 2022 , A37
Check for updates
Copyright
© California Institute of Technology, 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bae, J.H., Yoo, J.Y. & Choi, H. 2005 Direct numerical simulation of turbulent supercritical flows with heat transfer. Phys. Fluids 17, 105104.CrossRefGoogle Scholar
Bae, J.H., Yoo, J.Y. & McEligot, D.M. 2008 Direct numerical simulation of heated $\mathrm {CO_{2}}$ flows at supercritical pressure in a vertical annulus at $Re=8900$. Phys. Fluids 20, 055108.CrossRefGoogle Scholar
Ben Dakhlia, R., Giovangigli, V. & Rosner, D.E. 2002 Soret effects in laminar counterflow spray diffusion flames. Combust. Theor. Model. 6, 1–17.CrossRefGoogle Scholar
Castiglioni, G. & Bellan, J. 2018 On models for predicting thermodynamic regimes in high-pressure turbulent mixing and combustion of multi-species mixtures. J. Fluid Mech. 843, 536–574.CrossRefGoogle Scholar
Clusius, K. & Dickel, G. 1938 New process for separation of gas mixture and isotopes. Naturewiss 26, 546.CrossRefGoogle Scholar
Duan, L., Beekman, I. & Martín, M.P. 2010 Direct numerical simulation of hypersonic turbulent boundary layers. Part 2. Effect of wall temperature. J. Fluid Mech. 655, 419–445.CrossRefGoogle Scholar
Duan, L., Beekman, I. & Martín, M.P. 2011 Direct numerical simulation of hypersonic turbulent boundary layers. Part 3. Effect of Mach number. J. Fluid Mech. 672, 245–267.CrossRefGoogle Scholar
Duncan, J.B. & Toor, H.L. 1962 An experimental study of three component gas diffusion. AIChE J. 8 (1), 38–41.CrossRefGoogle Scholar
Ern, A. & Giovangigli, V. 1998 Thermal diffusion effects in hydrogen–air and methane–air flames. Combust. Theor. Model. 2, 349–372.CrossRefGoogle Scholar
Faith, L.E., Ackerman, G.H. & Henderson, H.T. 1971 Heat sink capability of jet a fuel: heat transfer and coking studies. S-14115, NASA CR-72951. Shell Development Co.Google Scholar
Gaitonde, D.V. & Visbal, M.R. 1998 High-order schemes for Navier–Stokes equations: algorithm and implementation into FDL3DI. In Air Force Research Lab Wright-Patterson AFB OH Air Vehicles Directorate AFRL-VA-WP-TR-1998-3060.CrossRefGoogle Scholar
Garcia-Ybarra, P.L. & Castillo, J.L. 1997 Mass transfer dominated by thermal diffusion in laminar boundary layers. J. Fluid Mech. 336, 379–409.CrossRefGoogle Scholar
Grcar, J.F., Bell, J. & Day, M. 2009 The Soret effect in naturally propagating, premixed, lean, hydrogen–air flames. Proc. Combust. Inst. 32, 1173–1180.CrossRefGoogle Scholar
Guo, J., Yang, X.I.A. & Ihme, M. 2022 Structure of the thermal boundary layer in turbulent channel flows at transcritical conditions. J. Fluid Mech. 934, A45.CrossRefGoogle Scholar
Harstad, K. & Bellan, J. 2004 a Mixing rules for multicomponent mixture mass diffusion coefficients and thermal diffusion factors. J. Chem. Phys. 120, 5664–5673.CrossRefGoogle ScholarPubMed
Harstad, K. & Bellan, J. 2004 b High-pressure binary mass-diffusion coefficients for combustion applications. Ind. Engng Chem. Res. 43, 645–654.Google Scholar
Harstad, K., Miller, R.S. & Bellan, J. 1997 Efficient high-pressure state equations. AIChE J. 43, 1605–1610.CrossRefGoogle Scholar
Jones, R.C. & Furry, W.H. 1946 The separation of isotopes by thermal diffusion. Rev. Mod. Phys. 18, 151–224.Google Scholar
Kawai, S. 2019 Heated transcritical and unheated non-transcritical turbulent boundary layers at supercritical pressures. J. Fluid Mech. 865, 563–601.CrossRefGoogle Scholar
Kim, K., Hickey, J. & Scalo, C. 2019 Pseudophase change effects in turbulent channel flow under transcritical temperature conditions. J. Fluid Mech. 871, 52–91.Google Scholar
Knapp, H., Döring, R., Oellrich, L., Plöcker, U. & Prausnitz, J.M. 1982 Vapor-Liquid Equilibria for Mixtures of Low Boiling Substances, vol. VI. Dechema.Google Scholar
Kozul, M., Chung, D. & Monty, J.P. 2016 Direct numerical simulation of the incompressible temporally developing turbulent boundary layer. J. Fluid Mech. 796, 437–472.Google Scholar
Lee, J., Jung, S.Y., Sung, H.J. & Zaki, T.A. 2013 Effect of wall heating on turbulent boundary layers with temperature-dependent viscosity. J. Fluid Mech. 726, 196–225.CrossRefGoogle Scholar
Lele, S.K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Liu, V.C. 1959 On the separation of gas mixtures by suction of thermal diffusion boundary layer. Q. J. Mech. Appl. Maths 12, 1–13.Google Scholar
Ma, P.C., Yang, X.I.A. & Ihme, M. 2018 Structure of wall-bounded flows at transcritical conditions. Phys. Rev. Fluids 3, 034609.CrossRefGoogle Scholar
Martín, M.P. 2004 DNS of hypersonic turbulent boundary layers, 34th AIAA Fluid Dynamics Conference and Exhibit. AIAA Paper 2004-2337.CrossRefGoogle Scholar
Masi, E., Bellan, J., Harstad, K.G. & Okong'o, N.A. 2013 Multi-species turbulent mixing under supercritical-pressure conditions: modelling, direct numerical simulation and analysis revealing species spinodal decomposition. J. Fluid Mech. 721, 578–626.CrossRefGoogle Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.CrossRefGoogle Scholar
Muller, S.M. & Scheerer, D. 1991 A method to parallelize tridiagonal solvers. Parallel Comput. 17, 181–188.CrossRefGoogle Scholar
Nagano, Y. & Tagawa, M. 1988 Statistical characteristics of wall turbulence with a passive scalar. J. Fluid Mech. 196, 157–185.CrossRefGoogle Scholar
Nemati, H., Patel, A., Boersma, B.J. & Pecnik, R. 2015 Mean statistics of a heated turbulent pipe flow at supercritical pressure. Intl J. Heat Mass Transfer 83, 741–752.CrossRefGoogle Scholar
Nemati, H., Patel, A., Boersma, B.J. & Pecnik, R. 2016 The effect of thermal boundary conditions on forced convection heat transfer to fluids at supercritical pressure. J. Fluid Mech. 800, 531–556.CrossRefGoogle Scholar
Okong'o, N. & Bellan, J. 2002 Consistent boundary conditions for multicomponent real gas mixtures based on characteristics wave. J. Comput. Phys. 176, 330–344.CrossRefGoogle Scholar
Okong'o, N., Harstad, K. & Bellan, J. 2002 Direct numerical simulation of $\mathrm {O_{2} /H_{2}}$ temporal mixing layers under supercritical conditions. AIAA J. 40, 914–926.CrossRefGoogle Scholar
Park, G.I., Wallace, J.M., Wu, X. & Moin, P. 2012 Boundary layer turbulence in transitional and developed states. Phys. Fluids 24, 035105.CrossRefGoogle Scholar
Patel, A., Boersma, B.J. & Pecnik, R. 2016 The influence of near-wall density and viscosity gradients on turbulence in channel flows. J. Fluid Mech. 809, 793–820.CrossRefGoogle Scholar
Patel, A., Boersma, B.J. & Pecnik, R. 2017 Scalar statistics in variable property turbulent channel flows. Phys. Rev. Fluids 2, 084604.CrossRefGoogle Scholar
Peeters, J.W.R., Pecnik, R., Rohde, M., Hagen, T.H.J.J.V.D. & Boersma, B.J. 2016 Turbulence attenuation in simultaneously heated and cooled annular flows at supercritical pressure. J. Fluid Mech. 799, 505–540.CrossRefGoogle Scholar
Pirozzoli, S. & Bernardini, M. 2011 Turbulence in supersonic boundary layers at moderate Reynolds number. J. Fluid Mech. 688, 120–168.CrossRefGoogle Scholar
Rosner, D.E. & Arias-Zugasti, M. 2007 Soret-modified hydrocarbon mass transport across compressed nonisothermal gases. AIChE J. 53, 1879–1890.CrossRefGoogle Scholar
Saghir, M.Z., Jiang, C.G., Chacha, M., Yan, Y., Khawaja, M. & Pan, S. 2005 Thermodiffusion in porous media. In Transport Phenomena in Porous Media III (eds. D.B. Ingham & I. Pop), Chap. 9, pp. 227–260. Elsevier.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Sciacovelli, L. & Bellan, J. 2019 The influence of the chemical composition representation according to the number of species during mixing in high-pressure turbulent flows. J. Fluid Mech. 863, 293–340.CrossRefGoogle Scholar
Taylor, R. & Krishna, R. 1993 Multicomponent Mass Transfer. John Wiley & Sons.Google Scholar
Toki, T. & Bellan, J. 2021 Investigation of species-mass diffusion in binary-species boundary layers at high pressure using direct numerical simulations. J. Fluid Mech. 928, A18.CrossRefGoogle Scholar
Toki, T., Teramoto, S. & Okamoto, K. 2020 Velocity and temperature profiles in turbulent channel flow at supercritical pressure. J. Propul. Power 36, 3–13.CrossRefGoogle Scholar
Wallace, J.M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.CrossRefGoogle Scholar
Wallace, J.M., Eckelmann, H. & Brodkey, R.S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.CrossRefGoogle Scholar
Wan, T., Zhao, P., Liu, J., Wang, C. & Lei, M. 2020 Mean velocity and temperature scaling for near-wall turbulence with heat transfer at supercritical pressure. Phys. Fluids 32, 055103.Google Scholar
Yang, F., Law, C.K., Sung, C-J. & Zhang, H. 2010 A mechanistic study of Soret diffusion in hydrogen–air flames. Combust. Flame 157, 192–200.CrossRefGoogle Scholar
Zonta, F., Marchioli, C. & Soldati, A. 2012 Modulation of turbulence in forced convection by temperature-dependent viscosity. J. Fluid Mech. 697, 150–174.CrossRefGoogle Scholar