Published online by Cambridge University Press: 28 April 2021
We consider the evolution of the bulk bubble-size distribution  $N(a,t)$ of large bubbles (Weber number
$N(a,t)$ of large bubbles (Weber number  ${\textit {We}}\gg 1$) under free-surface entrainment described generally by an entrainment size distribution
${\textit {We}}\gg 1$) under free-surface entrainment described generally by an entrainment size distribution  $I(a)$ with power-law slope
$I(a)$ with power-law slope  $\gamma$ and large-radius cutoff
$\gamma$ and large-radius cutoff  $a_{max}$. Our main focus is the interaction between turbulence-driven fragmentation and free-surface entrainment, and, for simplicity, we ignore other mechanisms such as degassing, coalescence and dissolution. Of special interest are the equilibrium bulk distribution
$a_{max}$. Our main focus is the interaction between turbulence-driven fragmentation and free-surface entrainment, and, for simplicity, we ignore other mechanisms such as degassing, coalescence and dissolution. Of special interest are the equilibrium bulk distribution  $N_{eq}(a)$, with local power-law slope
$N_{eq}(a)$, with local power-law slope  $\tilde {\beta }_{eq}(a)$, and the time scale
$\tilde {\beta }_{eq}(a)$, and the time scale  $\tau _c$ to reach this equilibrium after initiation of entrainment. For bubble radii
$\tau _c$ to reach this equilibrium after initiation of entrainment. For bubble radii  $a\ll a_{max}$, we find two regimes for the dependence of
$a\ll a_{max}$, we find two regimes for the dependence of  $N_{eq}(a)$ on the entrainment distribution. There is a weak injection regime for
$N_{eq}(a)$ on the entrainment distribution. There is a weak injection regime for  $\gamma \ge -4$, where
$\gamma \ge -4$, where  $\tilde {\beta }_{eq}(a)=-10/3$ independent of the entrainment distribution; and a strong injection regime for
$\tilde {\beta }_{eq}(a)=-10/3$ independent of the entrainment distribution; and a strong injection regime for  $\gamma <-4$, where the power-law slope depends on
$\gamma <-4$, where the power-law slope depends on  $\gamma$ and is given by
$\gamma$ and is given by  $\tilde {\beta }_{eq}(a)=\gamma +2/3$. The weak regime provides a general explanation for the commonly observed
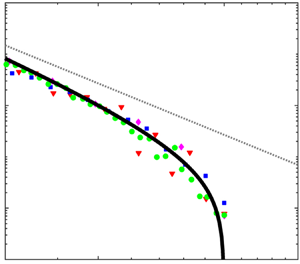
$\tilde {\beta }_{eq}(a)=\gamma +2/3$. The weak regime provides a general explanation for the commonly observed  $-10/3$ power law originally proposed by Garrett et al. (J. Phys. Oceanogr., vol. 30 (9), 2000, pp. 2163–2171), and suggests that different weak entrainment mechanisms can all lead to this result. For
$-10/3$ power law originally proposed by Garrett et al. (J. Phys. Oceanogr., vol. 30 (9), 2000, pp. 2163–2171), and suggests that different weak entrainment mechanisms can all lead to this result. For  $a\sim a_{max}$, we find that
$a\sim a_{max}$, we find that  $N_{eq}(a)$ exhibits a steepening deviation from a power law due to fragmentation and entrainment, similar to what has been observed, but here absent other mechanisms such as degassing. The evolution of
$N_{eq}(a)$ exhibits a steepening deviation from a power law due to fragmentation and entrainment, similar to what has been observed, but here absent other mechanisms such as degassing. The evolution of  $N(a,t)$ to
$N(a,t)$ to  $N_{eq}(a)$ is characterised by the critical time
$N_{eq}(a)$ is characterised by the critical time  $\tau _c \propto C_f \varepsilon ^{-1/3} {a_{max}}^{2/3}$, where
$\tau _c \propto C_f \varepsilon ^{-1/3} {a_{max}}^{2/3}$, where  $\varepsilon$ is the turbulence dissipation rate and
$\varepsilon$ is the turbulence dissipation rate and  $C_f$ is a new constant that quantifies the dependence on the daughter size distribution in a fragmentation event. For typical breaking waves,
$C_f$ is a new constant that quantifies the dependence on the daughter size distribution in a fragmentation event. For typical breaking waves,  $\tau _c$ can be quite small, limiting the time
$\tau _c$ can be quite small, limiting the time  $t\lesssim \tau _c$ when direct measurement of
$t\lesssim \tau _c$ when direct measurement of  $N(a,t)$ might provide information about the underlying entrainment size distribution.
$N(a,t)$ might provide information about the underlying entrainment size distribution.