Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2025-01-06T03:22:24.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of non-periodic portions of interface on Richtmyer–Meshkov instability

Published online by Cambridge University Press:  20 December 2018

Xisheng Luo Open the ORCID record for Xisheng Luo [Opens in a new window] ,
Yu Liang ,
Ting Si Open the ORCID record for Ting Si [Opens in a new window]  and
Zhigang Zhai Open the ORCID record for Zhigang Zhai [Opens in a new window]
Xisheng Luo
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230026, China
Yu Liang
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Ting Si
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Zhigang Zhai*
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The development of a non-periodic 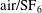$\text{air}\text{/}\text{SF}_{6}$ gaseous interface subjected to a planar shock wave is investigated experimentally and theoretically to evaluate the effects of the non-periodic portions of the interface on the Richtmyer–Meshkov instability. Experimentally, five kinds of discontinuous chevron-shaped interfaces with or without non-periodic portions are created by the extended soap film technique. The post-shock flows and the interface morphologies are captured by schlieren photography combined with a high-speed video camera. A periodic chevron-shaped interface, which is multi-modal (81 % fundamental mode and 19 % high-order modes), is first considered to evaluate the impulsive linear model and several typical nonlinear models. Then, the non-periodic chevron-shaped interfaces are investigated and the results show that the existence of non-periodic portions significantly changes the balanced position of the initial interface, and subsequently disables the nonlinear model which is applicable to the periodic chevron-shaped interface. A modified nonlinear model is proposed to consider the effects of the non-periodic portions. It turns out that the new model can predict the growth of the shocked non-periodic interface well. Finally, a method is established using spectrum analysis on the initial shape of the interface to separate its bubble structure and spike structure such that the new model can apply to any random perturbed interface. These findings can facilitate the understanding of the evolution of non-periodic interfaces which are more common in reality.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 309 - 327
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, U., Hecht, J., Ofer, D. & Shvarts, D. 1995 Power laws and similarity of Rayleigh–Taylor and Richtmyer–Meshkov mixing fronts. Phys. Rev. Lett. 74, 534–537.Google Scholar
Arnett, W. D., Bahcall, J. N., Kirshner, R. P. & Woosley, S. E. 1989 Supernova 1987A. Annu. Rev. Astron. Astrophys. 27, 629–700.Google Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.Google Scholar
Dimonte, G. & Ramaprabhu, P. 2010 Simulations and model of the nonlinear Richtmyer–Meshkov instability. Phys. Fluids 22, 014104.Google Scholar
Ding, J. C., Si, T., Chen, M. J., Zhai, Z. G., Lu, X. Y. & Luo, X. S. 2017 On the interaction of a planar shock with a three-dimensional light gas cylinder. J. Fluid Mech. 828, 289–317.Google Scholar
Hammer, N., Janka, H. & Müller, E. 2010 Three-dimensional simulations of mixing instabilities in Supernova explosions. Astrophys. J. 714, 1371–1385.Google Scholar
Hecht, J., Alon, U. & Shvarts, D. 1994 Potential flow models of Rayleigh–Taylor and Richtmyer–Meshkov bubble fronts. Phys. Fluids 6, 4019–4030.Google Scholar
Holder, D. A., Smith, A. V., Barton, C. J. & Youngs, D. L. 2003 Shock-tube experiments on Richtmyer–Meshkov instability growth using an enlarged double-bump perturbation. Laser Part. Beams 21, 411–418.Google Scholar
Jacobs, J. W. 1992 Shock-induced mixing of a light-gas cylinder. J. Fluid Mech. 234, 629–649.Google Scholar
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17, 034105.Google Scholar
Jourdan, G. & Houas, L. 2005 High-amplitude single-mode perturbation evolution at the Richtmyer–Meshkov instability. Phys. Rev. Lett. 95, 204502.Google Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. J. 122, 1–12.Google Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & Team, N. 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21, 020501.Google Scholar
Luo, X., Dong, P., Si, T. & Zhai, Z. 2016 The Richtmyer–Meshkov instability of a V shaped air/SF6 interface. J. Fluid Mech. 802, 186–202.Google Scholar
Luo, X., Zhai, Z., Si, T. & Yang, J. 2014 Experimental study on the interfacial instability induced by shock waves. Adv. Mech. 44, 201407.Google Scholar
McFarland, J., Greenough, J. & Ranjan, D. 2011 Computational parametric study of a Richtmyer–Meshkov instability for an inclined interface. Phys. Rev. E 84, 026303.Google Scholar
McFarland, J., Reilly, D., Black, W., Greenough, J. & Ranjan, D. 2015 Modal interactions between a large-wavelength inclined interface and small-wavelength multimode perturbations in a Richtmyer–Meshkov instability. Phys. Rev. E 92, 013023.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.Google Scholar
Mikaelian, K. O. 1994 Comment on ‘Quantitative theory of Richtmyer–Meshkov instability’. Phys. Rev. Lett. 73, 3177.Google Scholar
Mikaelian, K. O. 1998 Analytic approach to nonlinear Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Rev. Lett. 80, 508–511.Google Scholar
Mikaelian, K. O. 2003 Explicit expressions for the evolution of single-mode Rayleigh–Taylor and Richtmyer–Meshkov instabilities at arbitrary Atwood numbers. Phys. Rev. E 67, 026319.Google Scholar
Mikaelian, K. O. 2005 Richtmyer–Meshkov instability of arbitrary shapes. Phys. Fluids 17, 034101.Google Scholar
Mikaelian, K. O. 2008 Limitations and failures of the Layzer model for hydrodynamic instabilities. Phys. Rev. E 78, 015303.Google Scholar
Mohaghar, M., Carter, J., Musci, B., Reilly, D., McFarland, J. & Ranjan, D. 2017 Evaluation of turbulent mixing transition in a shock-driven variable-density flow. J. Fluid Mech. 831, 779–825.Google Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock–bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.Google Scholar
Sadot, O., Erez, L., Alon, U., Oron, D., Levin, L. A., Erez, G., Ben-Dor, G. & Shvarts, D. 1998 Study of nonlinear evolution of single-mode and two-bubble interaction under Richtmyer–Meshkov instability. Phys. Rev. Lett. 80, 1654–1657.Google Scholar
Shimoda, J., Inoue, T., Ohira, Y., Yamazaki, R., Bamba, A. & Vink, J. 2015 On cosmic-ray production efficiency at supernova remnant shocks propagating into realistic diffuse interstellar medium. Astrophys. J. 803, 98–103.Google Scholar
Vandenboomgaerde, M., Rouzier, P., Souffland, D., Biamino, L., Jourdan, G., Houas, L. & Mariani, C. 2018 Nonlinear growth of the converging Richtmyer–Meshkov instability in a conventional shock tube. Phys. Rev. Fluids 3, 014001.Google Scholar
Vandenboomgaerde, M., Souffland, D., Mariani, C., Biamino, L., Jourdan, G. & Houas, L. 2014 An experimental and numerical investigation of the dependency on the initial conditions of the Richtmyer–Meshkov instability. Phys. Fluids 26, 024109.Google Scholar
Velikovich, A., Herrmann, M. & Abarzhi, S. 2014 Perturbation theory and numerical modelling of weakly and moderately nonlinear dynamics of the incompressible Richtmyer–Meshkov instability. J. Fluid Mech. 751, 432–479.Google Scholar
Wang, M., Si, T. & Luo, X. 2013 Generation of polygonal gas interfaces by soap film for Richtmyer–Meshkov instability study. Exp. Fluids 54, 1427–1435.Google Scholar
Yang, J., Kubota, T. & Zukoski, E. E. 1994 A model for characterization of a vortex pair formed by shock passage over a light-gas inhomogeneity. J. Fluid Mech. 258, 217–244.Google Scholar
Yang, Q., Chang, J. & Bao, W. 2015 Richtmyer–Meshkov instability induced mixing enhancement in the scramjet combustor with a central strut. Adv. Mech. Engng 6, 1–7.Google Scholar
Zabusky, N. J. 1999 Vortex paradigm for accelerated inhomogeneous flows: visiometrics for the Rayleigh–Taylor and Richtmyer–Meshkov environments. Annu. Rev. Fluid Mech. 31, 495–536.Google Scholar
Zhai, Z., Dong, P., Si, T. & Luo, X. 2016 The Richtmyer–Meshkov instability of a V shaped air/helium interface subjected to a weak shock. Phys. Fluids 28, 082104.Google Scholar
Zhai, Z., Zou, L., Wu, Q. & Luo, X. 2018 Review of experimental Richtmyer–Meshkov instability in shock tube: from simple to complex. Proc. Inst. Mech. Engng Part C 232, 2830–2849.Google Scholar
Zhang, Q. & Guo, W. 2016 Universality of finger growth in two-dimensional Rayleigh–Taylor and Richtmyer–Meshkov instabilities with all density ratios. J. Fluid Mech. 786, 47–61.Google Scholar
Zhang, Q. & Sohn, S. I. 1996 An analytical nonlinear theory of Richtmyer–Meshkov instability. Phys. Lett. A 212, 149–155.Google Scholar