Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T06:37:45.377Z Has data issue: false hasContentIssue false
  • English
  • Français

The effects of forced small-wavelength, finite-bandwidth initial perturbations and miscibility on the turbulent Rayleigh–Taylor instability

Published online by Cambridge University Press:  07 December 2015

M. S. Roberts  and
J. W. Jacobs
M. S. Roberts*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
J. W. Jacobs
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

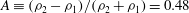Rayleigh–Taylor instability experiments are performed using both immiscible and miscible incompressible liquid combinations having a relatively large Atwood number of $A\equiv ({\it\rho}_{2}-{\it\rho}_{1})/({\it\rho}_{2}+{\it\rho}_{1})=0.48$. The liquid-filled tank is attached to a test sled that is accelerated downwards along a vertical rail system using a system of weights and pulleys producing approximately 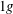$1g$ net acceleration. The tank is backlit and images are digitally recorded using a high-speed video camera. The experiments are either initiated with forced initial perturbations or are left unforced. The forced experiments have an initial perturbation imposed by vertically oscillating the liquid-filled tank to produce Faraday waves at the interface. The unforced experiments rely on random interfacial fluctuations, resulting from background noise, to seed the instability. The main focus of this study is to determine the effects of forced initial perturbations and the effects of miscibility on the growth parameter, ${\it\alpha}$. Measurements of the mixing-layer width, 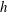$h$, are acquired, from which ${\it\alpha}$ is determined. It is found that initial perturbations of the form used in this study do not affect measured ${\it\alpha}$ values. However, miscibility is observed to strongly affect ${\it\alpha}$, resulting in a factor of two reduction in its value, a finding not previously observed in past experiments. In addition, all measured ${\it\alpha}$ values are found to be smaller than those obtained in previous experimental studies.

JFM classification

Convection: Buoyancy-driven instability Instability: Nonlinear instability Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 787 , 25 January 2016 , pp. 50 - 83
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anuchina, N. N., Kucherenko, Yu. A., Neuvazhaev, V. E., Ogibina, V. N., Shibarshov, L. I. & Yakovlev, V. G. 1978 Turbulent mixing at an accelerating interface between liquids of different density. Fluid Dyn. 13 (6), 916–920.Google Scholar
Bellman, R. & Pennington, R. H. 1954 Effects of surface tension and viscosity on Taylor instability. Q. Appl. Maths 12 (2), 151–162.CrossRefGoogle Scholar
Betti, R., Goncharov, V. N., McCrory, R. L. & Verdon, C. P. 1998 Growth rates of the ablative Rayleigh–Taylor instability in inertial confinement fusion. Phys. Plasmas 5 (5), 1446–1454.Google Scholar
Cabot, W. H. & Cook, A. W. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type-Ia supernovae. Nat. Phys. 2 (8), 562–568.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Clark, D. S., Haan, S. W., Cook, A. W., Edwards, M. J., Hammel, B. A., Koning, J. M. & Marinak, M. M. 2011 Short-wavelength and three-dimensional instability evolution in National Ignition Facility ignition capsule designs. Phys. Plasmas 18 (8), 082701.CrossRefGoogle Scholar
Cohen, I. M. & Kundu, P. K. 2004 Fluid Mechanics, 3rd edn. Elsevier.Google Scholar
Cole, R. L. & Tankin, R. S. 1973 Experimental study of Taylor instability. Phys. Fluids 16 (11), 1810–1815.CrossRefGoogle Scholar
Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–362.Google Scholar
Dalziel, S. B. 1993 Rayleigh–Taylor instability – experiments with image-analysis. Dyn. Atmos. Oceans 20 (1–2), 127–153.Google Scholar
Dalziel, S. B., Linden, P. F. & Youngs, D. L. 1999 Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.CrossRefGoogle Scholar
Dimonte, G. 2004 Dependence of turbulent Rayleigh–Taylor instability on initial perturbations. Phys. Rev. E 69 (5, Part 2), 056305.CrossRefGoogle ScholarPubMed
Dimonte, G., Morrison, J. J., Hulsey, S. D., Nelson, D., Weaver, S., Susoeff, A. R., Hawke, R. S., Schneider, M. B., Batteaux, J., Lee, D. & Ticehurst, J. 1996 A linear electric motor to study turbulent hydrodynamics. Rev. Sci. Instrum. 67 (1), 302–306.CrossRefGoogle Scholar
Dimonte, G., Ramaprabhu, P. & Andrews, M. J. 2007 Rayleigh–Taylor instability with complex acceleration history. Phys. Rev. E 76 (4, Part 2), 046313.CrossRefGoogle ScholarPubMed
Dimonte, G. & Schneider, M. 1996 Turbulent Rayleigh–Taylor instability experiments with variable acceleration. Phys. Rev. E 54 (4), 3740–3743.CrossRefGoogle ScholarPubMed
Dimonte, G. & Schneider, M. 2000 Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids 12 (2), 304–321.Google Scholar
Dimonte, G., Youngs, D. L., Dimits, A., Weber, S., Marinak, M., Wunsch, S., Garasi, C., Robinson, A., Andrews, M. J., Ramaprabhu, P. et al. 2004 A comparative study of the turbulent Rayleigh–Taylor instability using high-resolution three-dimensional numerical simulations: the Alpha-Group collaboration. Phys. Fluids 16 (5), 1668–1693.CrossRefGoogle Scholar
Duff, R., Harlow, F. & Hirt, C. 1962 Effects of diffusion on interface instability between gases. Phys. Fluids 5 (4), 417–425.Google Scholar
Emmons, H. W., Chang, C. T. & Watson, B. C. 1960 Taylor instability of finite surface waves. J. Fluid Mech. 7 (2), 177–193.Google Scholar
Fermi, E. & Neumann, J. V.1955 Taylor instability of incompressible liquids. United States Atomic Energy Commission: Unclassified, AECU-2979.Google Scholar
Ghasemizad, A., Zarringhalam, H. & Gholamzadeh, L. 2009 The investigation of Rayleigh–Taylor instability growth rate in inertial confinement fusion. J. Plasma Fusion Res. 8, 1234–1238.Google Scholar
Goncharov, V. N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88 (13), 134502.Google Scholar
Herrmann, M. C., Tabak, M. & Lindl, J. D. 2001 Ignition scaling laws and their application to capsule design. Phys. Plasmas 8 (5), 2296–2304.CrossRefGoogle Scholar
Jacobs, J. W. & Catton, I. 1988a Three-dimensional Rayleigh–Taylor instability. Part 1. Weakly nonlinear theory. J. Fluid Mech. 187, 329–352.Google Scholar
Jacobs, J. W. & Catton, I. 1988b Three-dimensional Rayleigh–Taylor instability. Part 2. Experiment. J. Fluid Mech. 187, 353–371.CrossRefGoogle Scholar
Jacobs, J. W. & Dalziel, S. B. 2005 Rayleigh–Taylor instability in complex stratifications. J. Fluid Mech. 542, 251–279.CrossRefGoogle Scholar
Kucherenko, Y. A., Pylaev, A. P., Balabin, S. I., Murzakov, V. D., Ardashova, R. I., Popov, V. N., Savel’ev, V. E., Komarov, O. R., Kozelkov, O. E., Tyaktev, A. A. et al. 1997a Experimental investigation into the behavior of inertial motion for different Atwood numbers. In Proceedings of the Sixth International Workshop on The Physics of Compressible Turbulent Mixing, pp. 282–288.Google Scholar
Kucherenko, Y. A., Pylaev, A. P., Murzakov, V. D., Belomestnih, A. V., Popov, V. N. & Tyaktev, A. A. 2001 Experimental study into Rayleigh–Taylor turbulent mixing zone heterogenous structure. In Proceedings of the Eighth International Workshop on The Physics of Compressible Turbulent Mixing, RFNC-VNIITF.Google Scholar
Kucherenko, Y. A., Pylaev, A. P., Murzakov, V. D., Popov, V. N., Komarov, O. R., Savelev, V. E., Cherret, R. & Haas, J. F. 1997b Experimental study into the asymptotic stage of the separation of the turbulized mixtures in gravitationally stable mode. Laser Part. Beams 15 (1), 17–23; Zababakhin’s Scientific Talks, Snezhinsk, Russia, 16–20 September 1995.CrossRefGoogle Scholar
Kucherenko, Y. A., Shibarshov, L. I., Chitaikin, V. I., Balabin, S. I. & Pylaev, A. P. 1991 Experimental study of the gravitational turbulent mixing self-similar mode. In Proceedings of the 3rd International Workshop on the Physics of Compressible Turbulent Mixing, pp. 427–454.Google Scholar
Lawrie, A. G. W. & Dalziel, S. B. 2011 Turbulent diffusion in tall tubes. I. Models for Rayleigh–Taylor instability. Phys. Fluids 23 (8), 085109.CrossRefGoogle Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. J. 122 (1), 1–12.Google Scholar
Lewis, D. J. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. 2. Proc. R. Soc. Lond. A 202 (1068), 81–96.Google Scholar
Linden, P. F. & Redondo, J. M. 1991 Molecular mixing in the Rayleigh–Taylor instability. Part I: Global mixing. Phys. Fluids A 3 (5), 1269–1277.Google Scholar
Mueschke, N. J., Schilling, O., Youngs, D. L. & Andrews, M. J. 2009 Measurements of molecular mixing in a high-Schmidt-number Rayleigh–Taylor mixing layer. J. Fluid Mech. 632, 17–48.Google Scholar
Neuvazhaev, V. E. & Yakovlev, V. G. 1976a Numerical gas-dynamical calculation of turbulent mixing of the interface. J. Comput. Math. Phys. USSR 16 (2), 154–165.Google Scholar
Neuvazhaev, V. E. & Yakovlev, V. G. 1976b Theory of turbulent mixing at the interface of fluids in a gravity field. J. Appl. Mech. Tech. Phys. 17 (4), 513–519.CrossRefGoogle Scholar
Olson, D. H. & Jacobs, J. W. 2009 Experimental study of Rayleigh–Taylor instability with a complex initial perturbation. Phys. Fluids 21 (3), 034103.CrossRefGoogle Scholar
Oron, D., Arazi, L., Kartoon, D., Rikanati, A., Alon, U. & Shvarts, D. 2001 Dimensionality dependence of the Rayleigh–Taylor and Richtmyer–Meshkov instability late-time scaling laws. Phys. Plasmas 8 (6), 2883–2889.Google Scholar
Parsons, P. W. & Estrada, F. J. 1942 Changes in volume on mixing solutions. Ind. Engng Chem. 34, 949–952.Google Scholar
Poling, B. 2001 The Properties of Gases and Liquids. McGraw-Hill.Google Scholar
Ramaprabhu, P. & Andrews, M. J. 2003 Simultaneous measurements of velocity and density in buoyancy-driven mixing. Exp. Fluids 34 (1), 98–106.CrossRefGoogle Scholar
Ramaprabhu, P. & Andrews, M. J. 2004 Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.CrossRefGoogle Scholar
Ramaprabhu, P., Dimonte, G. & Andrews, M. J. 2005 A numerical study of the influence of initial perturbations on the turbulent Rayleigh–Taylor instability. J. Fluid Mech. 536, 285–319.CrossRefGoogle Scholar
Ratafia, M. 1973 Experimental investigation of Rayleigh–Taylor instability. Phys. Fluids 16 (8), 1207–1210.Google Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. In Scientific Papers, vol. 2, pp. 200–207. Cambridge University Press.Google Scholar
Read, K. I. 1984 Experimental investigation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12 (1–3), 45–58.Google Scholar
Ristorcelli, J. R. & Clark, T. T. 2004 Rayleigh–Taylor turbulence: self-similar analysis and direct numerical simulations. J. Fluid Mech. 507, 213–253.CrossRefGoogle Scholar
Roberts, M. S.2012 Experiments and simulations on the incompressible, Rayleigh–Taylor instability with small wavelength initial perturbations. PhD thesis, The University of Arizona.Google Scholar
Schneider, M. B., Dimonte, G. & Remington, B. 1998 Large and small scale structure in Rayleigh–Taylor mixing. Phys. Rev. Lett. 80 (16), 3507–3510.Google Scholar
Settles, G. S. 1999 Schlieren and shadowgraph imaging in the great outdoors. In Proceedings of PSFVIP-2, PF302.Google Scholar
Sharp, D. H. 1984 An overview of Rayleigh–Taylor instability. Physica D 12 (1–3), 3–18.Google Scholar
Snider, D. M. & Andrews, M. J. 1994 Rayleigh–Taylor and shear-driven mixing with an unstable thermal stratification. Phys. Fluids 6 (10), 3324–3334.CrossRefGoogle Scholar
Tanaka, Y., Yamamoto, T., Satomi, Y., Kubota, H. & Makita, T. 1977 Specific volume and viscosity of ethanol–water mixtures under high pressure. Rev. Phys. Chem. Japan 47, 12–24.Google Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Waddell, J. T.1999 Experimental study of the Rayleigh–Taylor instability of miscible liquids. Master’s thesis, University of Arizona.Google Scholar
Waddell, J. T., Niederhaus, C. E. & Jacobs, J. W. 2001 Experimental study of the Rayleigh–Taylor instability: low Atwood number liquid system with single-mode initial perturbations. Phys. Fluids 13 (5), 1263–1273.Google Scholar
Wilkinson, J. P. & Jacobs, J. W. 2007 Experimental study of the single-mode three-dimensional Rayleigh–Taylor instability. Phys. Fluids 19 (12), 124102.Google Scholar
Youngs, D. 1984 Numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 32–44.CrossRefGoogle Scholar
Youngs, D. L. 1989 Modeling turbulent mixing by Rayleigh–Taylor instability. Physica D 37 (1–3), 270–287.Google Scholar
Youngs, D. L. 1991 Three-dimensional numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Phys. Fluids A 3 (5, Part 2), 1312–1320; International Symposium on Fluid Mechanics of Stirring and Mixing, University of California–San Diego, La Jolla, CA, 20–24 August 1990.Google Scholar
Youngs, D. L. 1994 Numerical-simulation of mixing by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Laser Part. Beams 12 (4), 725–750.Google Scholar
Youngs, D. L. & Read, K. I.1983, Experimental investigation of turbulent mixing by Rayleigh–Taylor instability. Atomic Weapons Research Establishment Report (O11/83).Google Scholar