Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ni, Rui
Voth, Greg A.
and
Ouellette, Nicholas T.
2014.
Extracting turbulent spectral transfer from under-resolved velocity fields.
Physics of Fluids,
Vol. 26,
Issue. 10,
Saint-Michel, B
Dubrulle, B
Marié, L
Ravelet, F
and
Daviaud, F
2014.
Influence of Reynolds number and forcing type in a turbulent von Kármán flow.
New Journal of Physics,
Vol. 16,
Issue. 6,
p.
063037.
Parsa, Shima
and
Voth, Greg A.
2014.
Inertial Range Scaling in Rotations of Long Rods in Turbulence.
Physical Review Letters,
Vol. 112,
Issue. 2,
Lucas, Sabrina
Moulin, Frédéric
and
Guizien, Katell
2016.
Oscillating grid mesocosm for studying oxygen dynamics under controlled unsteady turbulence.
Limnology and Oceanography: Methods,
Vol. 14,
Issue. 1,
p.
1.
Bos, Wouter J.T.
and
Rubinstein, Robert
2017.
Mixing in modulated turbulence. Analytical results.
Computers & Fluids,
Vol. 151,
Issue. ,
p.
102.
Carter, Douglas W.
and
Coletti, Filippo
2017.
Scale-to-scale anisotropy in homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 827,
Issue. ,
p.
250.
Ezeta, Rodrigo
Huisman, Sander G.
Sun, Chao
and
Lohse, Detlef
2018.
Turbulence strength in ultimate Taylor–Couette turbulence.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
397.
Carter, Douglas W.
and
Coletti, Filippo
2018.
Small-scale structure and energy transfer in homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 854,
Issue. ,
p.
505.
Verschoof, Ruben A.
te Nijenhuis, Arne K.
Huisman, Sander G.
Sun, Chao
and
Lohse, Detlef
2018.
Periodically driven Taylor–Couette turbulence.
Journal of Fluid Mechanics,
Vol. 846,
Issue. ,
p.
834.
Gauding, M.
Bode, M.
Denker, D.
Brahami, Y.
Danaila, L.
and
Varea, E.
2021.
On the combined effect of internal and external intermittency in turbulent non-premixed jet flames.
Proceedings of the Combustion Institute,
Vol. 38,
Issue. 2,
p.
2767.
Lalescu, Cristian C.
and
Wilczek, Michael
2021.
Transitions of turbulent superstructures in generalized Kolmogorov flow.
Physical Review Research,
Vol. 3,
Issue. 2,
Zhou, Ye
2021.
Turbulence theories and statistical closure approaches.
Physics Reports,
Vol. 935,
Issue. ,
p.
1.
Gauding, M.
Bode, M.
Brahami, Y.
Varea, É.
and
Danaila, L.
2021.
Self-similarity of turbulent jet flows with internal and external intermittency.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Baj, P.
Alves Portela, F.
and
Carter, D.W.
2022.
On the simultaneous cascades of energy, helicity, and enstrophy in incompressible homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 952,
Issue. ,
Vela-Martín, Alberto
2022.
The energy cascade as the origin of intense events in small-scale turbulence.
Journal of Fluid Mechanics,
Vol. 937,
Issue. ,
Lawson, John M.
and
Ganapathisubramani, Bharathram
2022.
Unsteady forcing of turbulence by a randomly actuated impeller array.
Experiments in Fluids,
Vol. 63,
Issue. 1,
Fuchs, André
Kharche, Swapnil
Patil, Aakash
Friedrich, Jan
Wächter, Matthias
and
Peinke, Joachim
2022.
An open source package to perform basic and advanced statistical analysis of turbulence data and other complex systems.
Physics of Fluids,
Vol. 34,
Issue. 10,
Berning, Hanna
and
Rösgen, Thomas
2023.
Suppression of large-scale azimuthal modulations in a von Kármán flow using random forcing.
Physics of Fluids,
Vol. 35,
Issue. 7,
Antonov, Nikolay V.
Hnatič, Michal
Honkonen, Juha
Kakin, Polina I.
Lučivjanský, Tomáš
and
Mižišin, Lukáš
2025.
Renormalized field theory for non-equilibrium systems.
La Rivista del Nuovo Cimento,
Bentkamp, Lukas
and
Wilczek, Michael
2025.
Temporal large-scale intermittency and its impact on the statistics of turbulence.
Journal of Fluid Mechanics,
Vol. 1004,
Issue. ,
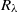 ${R}_{\lambda } $ up to 262, in which temporal variations in the large-scale energy input can be introduced by modulating the oscillating grid frequency. We find that the Kolmogorov constant for second-order longitudinal structure functions depends on the magnitude of the fluctuations in the large-scale energy input. We can quantitatively predict the measured change with a model based on Kolmogorov’s refined similarity theory. The effects of fluctuations of the energy input can also be observed using structure functions conditioned on the instantaneous large-scale velocity. A linear parametrization using the curvature of the conditional structure functions provides a fairly good match with the measured changes in the Kolmogorov constant. Conditional structure functions are found to provide a more sensitive measure of the presence of fluctuations in the large-scale energy input than inertial range scaling coefficients.
${R}_{\lambda } $ up to 262, in which temporal variations in the large-scale energy input can be introduced by modulating the oscillating grid frequency. We find that the Kolmogorov constant for second-order longitudinal structure functions depends on the magnitude of the fluctuations in the large-scale energy input. We can quantitatively predict the measured change with a model based on Kolmogorov’s refined similarity theory. The effects of fluctuations of the energy input can also be observed using structure functions conditioned on the instantaneous large-scale velocity. A linear parametrization using the curvature of the conditional structure functions provides a fairly good match with the measured changes in the Kolmogorov constant. Conditional structure functions are found to provide a more sensitive measure of the presence of fluctuations in the large-scale energy input than inertial range scaling coefficients.

