Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T02:25:33.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective slip boundary conditions for arbitrary one-dimensional surfaces

Published online by Cambridge University Press:  07 June 2012

Evgeny S. Asmolov  and
Olga I. Vinogradova
Evgeny S. Asmolov*
Affiliation:
A. N. Frumkin Institute of Physical Chemistry and Electrochemistry, Russian Academy of Sciences, 31 Leninsky Prospect, 119991 Moscow, Russia Central Aero-Hydrodynamic Institute, 140180 Zhukovsky, Moscow region, Russia Institute of Mechanics, M. V. Lomonosov Moscow State University, 119991 Moscow, Russia
Olga I. Vinogradova
Affiliation:
A. N. Frumkin Institute of Physical Chemistry and Electrochemistry, Russian Academy of Sciences, 31 Leninsky Prospect, 119991 Moscow, Russia Department of Physics, M. V. Lomonosov Moscow State University, 119991 Moscow, Russia DWI, RWTH Aachen, Forckenbeckstr. 50, 52056 Aachen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

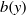In many applications it is advantageous to construct effective slip boundary conditions, which could fully characterize flow over patterned surfaces. Here we focus on laminar shear flows over smooth anisotropic surfaces with arbitrary scalar slip , varying in only one direction. We derive general expressions for eigenvalues of the effective slip-length tensor, and show that the transverse component is equal to half of the longitudinal one, with a two times larger local slip, . A remarkable corollary of this relation is that the flow along any direction of the one-dimensional surface can be easily determined, once the longitudinal component of the effective slip tensor is found from the known spatially non-uniform scalar slip.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Micro-/Nano-fluid dynamics: Microfluidics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 108 - 117
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Asmolov, E. S. 2008 Shear-induced self-diffusion in a wall-bounded dilute suspension. Phys. Rev. E 77, 66312.CrossRefGoogle Scholar
2. Asmolov, E. S., Belyaev, A. V. & Vinogradova, O. I. 2011 Drag force on a sphere moving towards an anisotropic super-hydrophobic plane. Phys. Rev. E 84, 026330.CrossRefGoogle Scholar
3. Bahga, S. S., Vinogradova, O. I. & Bazant, M. Z. 2010 Anisotropic electro-osmotic flow over super-hydrophobic surfaces. J. Fluid Mech. 644, 245–255.CrossRefGoogle Scholar
4. Bazant, M. Z. & Vinogradova, O. I. 2008 Tensorial hydrodynamic slip. J. Fluid Mech. 613, 125–134.CrossRefGoogle Scholar
5. Belyaev, A. V. & Vinogradova, O. I. 2010a Effective slip in pressure-driven flow past super-hydrophobic stripes. J. Fluid Mech. 652, 489–499.CrossRefGoogle Scholar
6. Belyaev, A. V. & Vinogradova, O. I. 2010b Hydrodynamic interaction with super-hydrophobic surfaces. Soft Matt. 6, 4563–4570.CrossRefGoogle Scholar
7. Belyaev, A. V. & Vinogradova, O. I. 2011 Electro-osmosis on anisotropic super-hydrophobic surfaces. Phys. Rev. Lett. 107, 098301.CrossRefGoogle Scholar
8. Cottin-Bizonne, C., Barentin, C. & Bocquet, L. 2012 Scaling laws for slippage on superhydrophobic fractal surfaces. Phys. Fluids 24, 012001.CrossRefGoogle Scholar
9. Cottin-Bizonne, C., Barentin, C., Charlaix, E., Bocquet, L. & Barrat, J. L. 2004 Dynamics of simple liquids at heterogeneous surfaces: molecular-dynamics simulations and hydrodynamic description. Eur. Phys. J. E 15, 427–438.CrossRefGoogle ScholarPubMed
10. Davis, A. M. J. & Lauga, E. 2010 Hydrodynamic friction of fakir-like superhydrophobic surfaces. J. Fluid Mech. 661, 402–411.CrossRefGoogle Scholar
11. Feuillebois, F., Bazant, M. Z. & Vinogradova, O. I. 2009 Effective slip over superhydrophobic surfaces in thin channels. Phys. Rev. Lett. 102, 026001.CrossRefGoogle ScholarPubMed
12. Kamrin, K., Bazant, M. Z. & Stone, H. A. 2010 Effective slip boundary conditions for arbitrary periodic surfaces: the surface mobility tensor. J. Fluid Mech. 658, 409–437.CrossRefGoogle Scholar
13. Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.CrossRefGoogle Scholar
14. Ng, C. O., Chu, H. C. W. & Wang, C. Y. 2010 On the effects of liquid–gas interfacial shear on slip flow through a parallel-plate channel with superhydrophobic grooved walls. Phys. Fluids 22, 102002.CrossRefGoogle Scholar
15. Ng, C. O. & Wang, C. Y. 2009 Stokes shear flow over a grating: implications for superhydrophobic slip. Phys. Fluids 21, 013602.CrossRefGoogle Scholar
16. Ng, C. O. & Wang, C. Y. 2011 Oscillatory flow through a channel with stick-slip walls: complex Navier’s slip length. Trans. ASME: J. Fluids Engng 133, 014502.Google Scholar
17. Philip, J. R. 1972 Flows satisfying mixed no-slip and no-shear conditions. Z. Angew. Math. Phys. 23, 353–372.CrossRefGoogle Scholar
18. Priezjev, N. V. 2011 Molecular diffusion and slip boundary conditions at smooth surfaces with periodic and random nanoscale textures. J. Chem. Phys. 135, 204704.CrossRefGoogle ScholarPubMed
19. Priezjev, N. V., Darhuber, A. A. & Troian, S. M. 2005 Slip behavior in liquid films on surfaces of patterned wettability. Phys. Rev. E 71, 041608.CrossRefGoogle ScholarPubMed
20. Sbragaglia, M. & Prosperetti, A. 2007 A note on the effective slip properties for microchannel flows with ultrahydrophobic surfaces. Phys. Fluids 19, 043603.CrossRefGoogle Scholar
21. Schmieschek, S., Belyaev, A. V., Harting, J. & Vinogradova, O. I. 2012 Tensorial slip of super-hydrophobic channels. Phys. Rev. E 85, 016324.CrossRefGoogle Scholar
22. Stone, H. A., Stroock, A. D. & Ajdari, A. 2004 Engineering flows in small devices. Annu. Rev. Fluid Mech. 36, 381–411.CrossRefGoogle Scholar
23. Teo, C. & Khoo, B. 2009 Analysis of Stokes flow in microchannels with superhydrophobic surfaces containing a periodic array of micro-grooves. Microfluid Nanofluid 7, 353.CrossRefGoogle Scholar
24. Vinogradova, O. I. & Belyaev, A. V. 2011 Wetting, roughness and flow boundary conditions. J. Phys.: Condens. Matt. 23, 184104.Google ScholarPubMed