Article contents
Effect of wall suction on rotating disk absolute instability
Published online by Cambridge University Press: 24 February 2016
Abstract
This research investigates the effect of uniform suction on the absolute instability of Type I cross-flow modes in the boundary layer on a rotating disk. Specifically, it is designed to investigate whether wall suction would transform the absolute instability into a global mode, as first postulated in the numerical simulations of Davies & Carpenter (J. Fluid Mech., vol. 486, 2003, pp. 287–329). The disk is designed so that with a suction parameter of 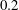 $0.2$, the radial location of the absolute instability critical Reynolds number,
$0.2$, the radial location of the absolute instability critical Reynolds number, 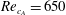 $Re_{c_{A}}=650$, occurs on the disk. Wall suction is applied from
$Re_{c_{A}}=650$, occurs on the disk. Wall suction is applied from 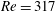 $Re=317$ to 696.5. The design for wall suction follows that of Gregory & Walker (J. Fluid Mech., 1960, pp. 225–234) where an array of holes through the disk communicate between the measurement side of the disk and the underside of the disk which is inside of an enclosure that is maintained at a slight vacuum. The enclosure pressure is adjustable so that a range of suction or blowing parameters can be investigated. The holes in the measurement surface are covered by a compressed wire porous mesh to aid in uniformizing the suction on the measurement surface of the disk. The mesh is covered by a thin porous high-density polyethylene sheet featuring a
$Re=317$ to 696.5. The design for wall suction follows that of Gregory & Walker (J. Fluid Mech., 1960, pp. 225–234) where an array of holes through the disk communicate between the measurement side of the disk and the underside of the disk which is inside of an enclosure that is maintained at a slight vacuum. The enclosure pressure is adjustable so that a range of suction or blowing parameters can be investigated. The holes in the measurement surface are covered by a compressed wire porous mesh to aid in uniformizing the suction on the measurement surface of the disk. The mesh is covered by a thin porous high-density polyethylene sheet featuring a 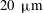 $20~{\rm\mu}\text{m}$ pore size which provides a smooth finely porous surface. A companion numerical simulation is performed to investigate the effect that the size and vacuum pressure of the underside enclosure have on the uniformity of the measurement surface suction. Temporal disturbances are introduced using the method of Othman & Corke (J. Fluid Mech., 2006, pp. 63–94). The results document the evolution of disturbance wavepackets in space and time. These show a temporal growth of the wavepackets as the location of the absolute instability is approached which is in strong contrast to the temporal evolution without suction observed by Othman and Corke. The results appear to support the effect of wall suction on the absolute instability postulated by Thomas (PhD thesis, 2007, Cardiff University, UK) and Thomas & Davies (J. Fluid Mech., vol. 663, 2010, pp. 401–433).
$20~{\rm\mu}\text{m}$ pore size which provides a smooth finely porous surface. A companion numerical simulation is performed to investigate the effect that the size and vacuum pressure of the underside enclosure have on the uniformity of the measurement surface suction. Temporal disturbances are introduced using the method of Othman & Corke (J. Fluid Mech., 2006, pp. 63–94). The results document the evolution of disturbance wavepackets in space and time. These show a temporal growth of the wavepackets as the location of the absolute instability is approached which is in strong contrast to the temporal evolution without suction observed by Othman and Corke. The results appear to support the effect of wall suction on the absolute instability postulated by Thomas (PhD thesis, 2007, Cardiff University, UK) and Thomas & Davies (J. Fluid Mech., vol. 663, 2010, pp. 401–433).
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 2
- Cited by



