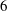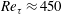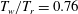1 Introduction
An understanding of the physics of pressure fluctuations induced by high-speed turbulent boundary layers is important to the structural design of hypersonic vehicles and to the testing and evaluation of hypersonic vehicles in noisy hypersonic facilities. The fluctuating surface pressure on vehicle surfaces is responsible for vibrational load and may lead to damaging effects such as flutter. The free-stream pressure fluctuations radiated from the turbulent boundary layer on the nozzle wall of conventional hypersonic wind tunnels give rise to tunnel noise that has first-order impact on laminar–turbulent transition in the tunnel. Given that the surface temperatures of hypersonic flight vehicles are typically significantly lower than the adiabatic wall temperature and that practical hypersonic facilities for testing and evaluating hypersonic vehicles are designed to have a non-adiabatic turbulent boundary layer on the nozzle wall, it is of practical importance to investigate wall-temperature effects on hypersonic turbulent boundary layers and their induced pressure fluctuations.
To date, there is limited literature on the effects of wall cooling on high-speed turbulent boundary layers. Most of the available measurements are restricted to basic turbulence quantities, such as the skin friction and Stanton number, and the mean and root mean square (r.m.s.) fluctuations of velocity and temperature (Fernholz & Finley Reference Fernholz and Finley1980; Smits & Dussauge Reference Smits and Dussauge2006). Existing numerical studies are largely focused on the effect of wall cooling on the distribution and scaling of velocity fluctuations and the relationships between temperature and velocity fields at a Mach number of 5 or less (Maeder Reference Maeder2000; Duan, Beekman & Martín Reference Duan, Beekman and Martín2010; Shahab et al.
Reference Shahab, Lehnasch, GatskiEmail and Comte2011; Chu, Zhang & Lu Reference Chu, Zhang and Lu2013; Zhang et al.
Reference Zhang, Bi, Hussain and She2014; Hadjadj et al.
Reference Hadjadj, Ben-Nasr, Shadloo and Chaudhuri2015; Shadloo, Hadjadj & Hussain Reference Shadloo, Hadjadj and Hussain2015; Trettel & Larsson Reference Trettel and Larsson2016). For example, Duan et al. (Reference Duan, Beekman and Martín2010) performed direct numerical simulations (DNS) of turbulent boundary layers at Mach 5 over a broad range of wall-to-recovery temperature ratios (
![]() $T_{w}/T_{r}=0.18$
–1.0) and focused on assessing the validity of Morkonvin’s hypothesis in the high-Mach-number cold-wall regime. Zhang et al. (Reference Zhang, Bi, Hussain and She2014) studied the coupling between the thermal and velocity fields of compressible wall-bounded turbulent flows and introduced a generalized Reynolds analogy that explicitly accounts for finite wall heat flux for cold-wall boundary layers. Hadjadj et al. (Reference Hadjadj, Ben-Nasr, Shadloo and Chaudhuri2015) and Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015) conducted detailed analyses of the effect of wall temperature on the statistical behaviour of turbulent boundary layers at Mach 2. Bowersox (Reference Bowersox2009) and Poggie (Reference Poggie2015) studied the modelling of turbulent energy flux in adiabatic and cold-wall turbulent boundary layers. Trettel & Larsson (Reference Trettel and Larsson2016) introduced a new mean-velocity scaling for compressible wall turbulence with heat transfer; this new scaling achieved excellent collapse of the mean-velocity profile at different Reynolds numbers, Mach numbers and rates of wall heat transfer.
$T_{w}/T_{r}=0.18$
–1.0) and focused on assessing the validity of Morkonvin’s hypothesis in the high-Mach-number cold-wall regime. Zhang et al. (Reference Zhang, Bi, Hussain and She2014) studied the coupling between the thermal and velocity fields of compressible wall-bounded turbulent flows and introduced a generalized Reynolds analogy that explicitly accounts for finite wall heat flux for cold-wall boundary layers. Hadjadj et al. (Reference Hadjadj, Ben-Nasr, Shadloo and Chaudhuri2015) and Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015) conducted detailed analyses of the effect of wall temperature on the statistical behaviour of turbulent boundary layers at Mach 2. Bowersox (Reference Bowersox2009) and Poggie (Reference Poggie2015) studied the modelling of turbulent energy flux in adiabatic and cold-wall turbulent boundary layers. Trettel & Larsson (Reference Trettel and Larsson2016) introduced a new mean-velocity scaling for compressible wall turbulence with heat transfer; this new scaling achieved excellent collapse of the mean-velocity profile at different Reynolds numbers, Mach numbers and rates of wall heat transfer.
As far as the boundary-layer-induced pressure fluctuations are concerned, the body of available data is even more scarce. Experimental measurements consist largely of those at the wall using surface-mounted pressure transducers (Kistler & Chen Reference Kistler and Chen1963; Fernholz et al. Reference Fernholz, Dussauge, Finlay, Smits and Reshotko1989; Beresh et al. Reference Beresh, Henfling, Spillers and Pruett2011). Previous DNS studies of pressure fluctuations induced by high-speed turbulent boundary layers have focused on boundary layers with adiabatic or nearly adiabatic walls (Bernardini & Pirozzoli Reference Bernardini and Pirozzoli2011; Di Marco et al. Reference Di Marco, Camussi, Bernardini and Pirozzoli2013; Duan, Choudhari & Wu Reference Duan, Choudhari and Wu2014; Duan, Choudhari & Zhang Reference Duan, Choudhari and Zhang2016). To the best of the knowledge of the authors, no existing studies have been conducted in the high-Mach-number cold-wall regime that provide the off-wall fluctuating pressure field including the free-stream acoustic pressure fluctuations. As a result, a comprehensive understanding of the free-stream disturbance field and its dependence on boundary-layer parameters (e.g. free-stream Mach number, wall temperature and Reynolds number) is still lacking.
The objective of the current paper is to investigate the dependence of boundary-layer-induced pressure fluctuations on wall temperature for hypersonic Mach numbers. In a previous paper by the present authors (Duan et al.
Reference Duan, Choudhari and Zhang2016), the successful application of DNS in capturing the global fluctuating pressure field has been demonstrated for a spatially developing flat-plate nominally Mach 6 turbulent boundary layer with a wall-to-recovery temperature ratio of
![]() $T_{w}/T_{r}=0.76$
. A new DNS dataset at Mach 6 with a different wall temperature (
$T_{w}/T_{r}=0.76$
. A new DNS dataset at Mach 6 with a different wall temperature (
![]() $T_{w}/T_{r}=0.25$
) from the previous Mach 6 data (Duan et al.
Reference Duan, Choudhari and Zhang2016) is introduced for the study of wall-temperature effects. The effect of wall temperature on single- and multi-point statistics of the computed pressure fluctuations at multiple wall-normal locations (including the inner layer, the log layer, the outer layer and the free stream) is reported, including the intensity, frequency spectra, space–time correlations and propagation velocities.
$T_{w}/T_{r}=0.25$
) from the previous Mach 6 data (Duan et al.
Reference Duan, Choudhari and Zhang2016) is introduced for the study of wall-temperature effects. The effect of wall temperature on single- and multi-point statistics of the computed pressure fluctuations at multiple wall-normal locations (including the inner layer, the log layer, the outer layer and the free stream) is reported, including the intensity, frequency spectra, space–time correlations and propagation velocities.
The remainder of this paper is structured as follows. The flow conditions selected for numerical simulation and the numerical method used are outlined in § 2. Section 4 is focused on an analysis of statistical and structural features of pressure fluctuations at multiple wall-normal locations, highlighting their dependence on the wall temperature. The various statistics examined include pressure-fluctuation intensities, power spectral densities, two-point pressure correlations, propagation speeds and acoustic sources. Conclusions from the study are presented in § 5.
Table 1. Free-stream conditions for Mach 6 DNS of turbulent boundary layers. The working fluid is assumed to be a perfect gas.
2 Simulation details
Direct numerical simulations are performed for zero-pressure-gradient cold-wall turbulent boundary layers with a free-stream Mach number of 5.86. Two DNS cases (M6Tw025 and M6Tw076) with the same free-stream conditions but different wall temperatures are examined, with the M6Tw076 case corresponding to the previous simulation by Duan et al. (Reference Duan, Choudhari and Zhang2016). Table 1 outlines the free-stream conditions for the simulations, including the free-stream velocity
![]() $U_{\infty }$
, density
$U_{\infty }$
, density
![]() $\unicode[STIX]{x1D70C}_{\infty }$
and temperature
$\unicode[STIX]{x1D70C}_{\infty }$
and temperature
![]() $T_{\infty }$
. The free-stream conditions are representative of those at the nozzle exit of the Purdue Mach 6 Quiet Tunnel (BAM6QT) under noisy operation (Schneider Reference Schneider2001; Steen Reference Steen2010). Table 2 lists the values of the mean boundary-layer parameters at the selected downstream location (
$T_{\infty }$
. The free-stream conditions are representative of those at the nozzle exit of the Purdue Mach 6 Quiet Tunnel (BAM6QT) under noisy operation (Schneider Reference Schneider2001; Steen Reference Steen2010). Table 2 lists the values of the mean boundary-layer parameters at the selected downstream location (
![]() $x_{a}$
) for statistical analysis, including the momentum thickness
$x_{a}$
) for statistical analysis, including the momentum thickness
![]() $\unicode[STIX]{x1D703}$
, shape factor
$\unicode[STIX]{x1D703}$
, shape factor
![]() $H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}$
(where
$H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}$
(where
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
denotes the local displacement thickness), boundary-layer thickness
$\unicode[STIX]{x1D6FF}^{\ast }$
denotes the local displacement thickness), boundary-layer thickness
![]() $\unicode[STIX]{x1D6FF}$
, friction velocity
$\unicode[STIX]{x1D6FF}$
, friction velocity
![]() $u_{\unicode[STIX]{x1D70F}}=\sqrt{\unicode[STIX]{x1D70F}_{w}/\bar{\unicode[STIX]{x1D70C}}_{w}}$
, viscous length
$u_{\unicode[STIX]{x1D70F}}=\sqrt{\unicode[STIX]{x1D70F}_{w}/\bar{\unicode[STIX]{x1D70C}}_{w}}$
, viscous length
![]() $z_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}_{w}/\unicode[STIX]{x1D70C}_{w}u_{\unicode[STIX]{x1D70F}}$
and different definitions of the Reynolds number, namely
$z_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D707}_{w}/\unicode[STIX]{x1D70C}_{w}u_{\unicode[STIX]{x1D70F}}$
and different definitions of the Reynolds number, namely
![]() $Re_{\unicode[STIX]{x1D703}}\equiv \unicode[STIX]{x1D70C}_{\infty }U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D707}_{\infty }$
,
$Re_{\unicode[STIX]{x1D703}}\equiv \unicode[STIX]{x1D70C}_{\infty }U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D707}_{\infty }$
,
![]() $Re_{\unicode[STIX]{x1D70F}}\equiv \unicode[STIX]{x1D70C}_{w}u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D707}_{w}$
and
$Re_{\unicode[STIX]{x1D70F}}\equiv \unicode[STIX]{x1D70C}_{w}u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D707}_{w}$
and
![]() $Re_{\unicode[STIX]{x1D6FF}2}\equiv \unicode[STIX]{x1D70C}_{\infty }U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D707}_{w}$
. Throughout this paper, the subscripts
$Re_{\unicode[STIX]{x1D6FF}2}\equiv \unicode[STIX]{x1D70C}_{\infty }U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D707}_{w}$
. Throughout this paper, the subscripts
![]() $\infty$
and
$\infty$
and
![]() $w$
will be used to denote quantities in the free stream and at the wall respectively. The viscosity
$w$
will be used to denote quantities in the free stream and at the wall respectively. The viscosity
![]() $\unicode[STIX]{x1D707}$
is calculated using Sutherland’s law,
$\unicode[STIX]{x1D707}$
is calculated using Sutherland’s law,
![]() $\unicode[STIX]{x1D707}=C_{1}T^{3/2}/(T+C_{2})$
, with constants
$\unicode[STIX]{x1D707}=C_{1}T^{3/2}/(T+C_{2})$
, with constants
![]() $C_{1}=1.458\times 10^{-6}$
and
$C_{1}=1.458\times 10^{-6}$
and
![]() $C_{2}=110.4$
. The wall temperature
$C_{2}=110.4$
. The wall temperature
![]() $T_{w}$
for the case M6Tw076 is similar to that at the nozzle wall of BAM6QT, corresponding to a wall-temperature ratio of
$T_{w}$
for the case M6Tw076 is similar to that at the nozzle wall of BAM6QT, corresponding to a wall-temperature ratio of
![]() $T_{w}/T_{r}\approx 0.76$
, with the recovery temperature estimated as
$T_{w}/T_{r}\approx 0.76$
, with the recovery temperature estimated as
![]() $T_{r}=T_{\infty }(1+r(\unicode[STIX]{x1D6FE}-1)M_{\infty }^{2}/2)$
based on a recovery factor of
$T_{r}=T_{\infty }(1+r(\unicode[STIX]{x1D6FE}-1)M_{\infty }^{2}/2)$
based on a recovery factor of
![]() $r=0.89$
. Case M6Tw025 has the same free-stream conditions and Reynolds number,
$r=0.89$
. Case M6Tw025 has the same free-stream conditions and Reynolds number,
![]() $Re_{\unicode[STIX]{x1D70F}}$
, as case M6Tw076 but a lower wall temperature (
$Re_{\unicode[STIX]{x1D70F}}$
, as case M6Tw076 but a lower wall temperature (
![]() $T_{w}/T_{r}\approx 0.25$
) which is more likely to be encountered in high-altitude flight. Thus, by comparing the results of cases M6Tw025 and M6Tw076, the effect of wall cooling on the pressure fluctuations can be investigated at a fixed Reynolds number
$T_{w}/T_{r}\approx 0.25$
) which is more likely to be encountered in high-altitude flight. Thus, by comparing the results of cases M6Tw025 and M6Tw076, the effect of wall cooling on the pressure fluctuations can be investigated at a fixed Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}$
.
$Re_{\unicode[STIX]{x1D70F}}$
.
Wall cooling causes a change in both the boundary-layer thickness and the fluid properties across the boundary layer. Experiments and numerical data suggest that a single Reynolds number is not sufficient to characterize the flow (Smits Reference Smits1991; Lele Reference Lele1994). However, what definition of the Reynolds number is ‘correct’ for assessing the effects of wall cooling is still an open question, and the choice of that definition mainly depends on researcher preference and the research objective (Shadloo et al.
Reference Shadloo, Hadjadj and Hussain2015). For instance, out of the few existing DNS studies on the effect of wall temperature, Maeder (Reference Maeder2000), Lagha et al. (Reference Lagha, Kim, Eldredge and Zhong2011) and Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015) have chosen to match
![]() $Re_{\unicode[STIX]{x1D70F}}$
for reporting their data; Duan et al. (Reference Duan, Beekman and Martín2010) and Chu et al. (Reference Chu, Zhang and Lu2013) have chosen to match
$Re_{\unicode[STIX]{x1D70F}}$
for reporting their data; Duan et al. (Reference Duan, Beekman and Martín2010) and Chu et al. (Reference Chu, Zhang and Lu2013) have chosen to match
![]() $Re_{\unicode[STIX]{x1D6FF}2}$
; Shahab et al. (Reference Shahab, Lehnasch, GatskiEmail and Comte2011) have chosen to match
$Re_{\unicode[STIX]{x1D6FF}2}$
; Shahab et al. (Reference Shahab, Lehnasch, GatskiEmail and Comte2011) have chosen to match
![]() $Re_{\unicode[STIX]{x1D703}}$
. In addition, Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015) compared the effects of choosing different definitions of the Reynolds number (
$Re_{\unicode[STIX]{x1D703}}$
. In addition, Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015) compared the effects of choosing different definitions of the Reynolds number (
![]() $Re_{\unicode[STIX]{x1D70F}}$
,
$Re_{\unicode[STIX]{x1D70F}}$
,
![]() $Re_{\unicode[STIX]{x1D6FF}2}$
,
$Re_{\unicode[STIX]{x1D6FF}2}$
,
![]() $Re_{\unicode[STIX]{x1D703}}$
) on the turbulence statistics and showed that
$Re_{\unicode[STIX]{x1D703}}$
) on the turbulence statistics and showed that
![]() $Re_{\unicode[STIX]{x1D70F}}$
performs best in collapsing the first- and second-order statistical moments for boundary layers with different wall heat transfer values. In the current study, we have chosen to match
$Re_{\unicode[STIX]{x1D70F}}$
performs best in collapsing the first- and second-order statistical moments for boundary layers with different wall heat transfer values. In the current study, we have chosen to match
![]() $Re_{\unicode[STIX]{x1D70F}}$
based partially on the findings of Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015). This selection of the Reynolds number is also due to our decisions with regard to grid resolutions and the limited extent of the computational domain.
$Re_{\unicode[STIX]{x1D70F}}$
based partially on the findings of Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015). This selection of the Reynolds number is also due to our decisions with regard to grid resolutions and the limited extent of the computational domain.
Table 2. Boundary-layer properties at the station (
![]() $x_{a}$
) selected for the analysis of the pressure field (
$x_{a}$
) selected for the analysis of the pressure field (
![]() $x_{a}=88.6\unicode[STIX]{x1D6FF}_{i}$
for case M6Tw025 and
$x_{a}=88.6\unicode[STIX]{x1D6FF}_{i}$
for case M6Tw025 and
![]() $x_{a}=54.1\unicode[STIX]{x1D6FF}_{i}$
for case M6Tw076, with
$x_{a}=54.1\unicode[STIX]{x1D6FF}_{i}$
for case M6Tw076, with
![]() $\unicode[STIX]{x1D6FF}_{i}$
being the boundary-layer thickness at the domain inlet).
$\unicode[STIX]{x1D6FF}_{i}$
being the boundary-layer thickness at the domain inlet).
The details of the DNS methodology, including numerical methods and initial and boundary conditions, have been documented in our previous papers (Duan et al. Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016). The DNS methodology has been extensively validated against experiments and existing numerical simulations for capturing boundary-layer-induced pressure fluctuations at supersonic/hypersonic speeds (Duan et al. Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016). In particular, the computational predictions for the mean-velocity profiles and surface pressure spectrum are in good agreement with experimental measurements for case M6Tw076 (Duan et al. Reference Duan, Choudhari and Zhang2016).
Figure 1 shows the computational set-up for case M6Tw025, which parallels that of case M6Tw076 documented in Duan et al. (Reference Duan, Choudhari and Zhang2016). The computational domain size and grid resolution are determined based on the lessons learnt from Duan et al. (Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016), as summarized in table 3. The streamwise length
![]() $L_{x}$
is adjusted to ensure that the turbulence fluctuations are uncorrelated and minimal spurious correlation can be introduced due to the inflow turbulence generation. The streamwise domain size is also large enough so that the free-stream acoustic field has gone through the transient adjustment due to recycled inflow and has re-established equilibrium at the downstream location selected for statistical analysis (
$L_{x}$
is adjusted to ensure that the turbulence fluctuations are uncorrelated and minimal spurious correlation can be introduced due to the inflow turbulence generation. The streamwise domain size is also large enough so that the free-stream acoustic field has gone through the transient adjustment due to recycled inflow and has re-established equilibrium at the downstream location selected for statistical analysis (
![]() $x_{a}=88.6\unicode[STIX]{x1D6FF}_{i}$
). It can be shown that the pressure fluctuations both at the wall and in the free stream for case M6Tw025 have become homogeneous in the streamwise direction after
$x_{a}=88.6\unicode[STIX]{x1D6FF}_{i}$
). It can be shown that the pressure fluctuations both at the wall and in the free stream for case M6Tw025 have become homogeneous in the streamwise direction after
![]() $x/\unicode[STIX]{x1D6FF}_{i}\approx 60$
. Uniform grid spacings are used in the streamwise and spanwise directions. The grids in the wall-normal direction are clustered in the boundary layer with
$x/\unicode[STIX]{x1D6FF}_{i}\approx 60$
. Uniform grid spacings are used in the streamwise and spanwise directions. The grids in the wall-normal direction are clustered in the boundary layer with
![]() $\unicode[STIX]{x0394}z^{+}=0.46$
at the wall, and are kept uniform with
$\unicode[STIX]{x0394}z^{+}=0.46$
at the wall, and are kept uniform with
![]() $\unicode[STIX]{x0394}z^{+}\approx 5$
in the free stream until up to approximately
$\unicode[STIX]{x0394}z^{+}\approx 5$
in the free stream until up to approximately
![]() $8\unicode[STIX]{x1D6FF}_{i}$
or
$8\unicode[STIX]{x1D6FF}_{i}$
or
![]() $3.3\unicode[STIX]{x1D6FF}$
, where
$3.3\unicode[STIX]{x1D6FF}$
, where
![]() $\unicode[STIX]{x1D6FF}_{i}$
and
$\unicode[STIX]{x1D6FF}_{i}$
and
![]() $\unicode[STIX]{x1D6FF}$
represent the mean boundary-layer thickness based on
$\unicode[STIX]{x1D6FF}$
represent the mean boundary-layer thickness based on
![]() $\overline{u}/U_{\infty }=0.99$
at the inflow boundary and at the selected downstream location
$\overline{u}/U_{\infty }=0.99$
at the inflow boundary and at the selected downstream location
![]() $x_{a}$
respectively. For the selected grid resolution, the wavelength of the highest-frequency spectral components of free-stream pressure fluctuations (corresponding to
$x_{a}$
respectively. For the selected grid resolution, the wavelength of the highest-frequency spectral components of free-stream pressure fluctuations (corresponding to
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }\approx 15$
, as shown in § 4.2) is discretized with at least nine points in the streamwise direction and 12 points in the wall-normal direction.
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }\approx 15$
, as shown in § 4.2) is discretized with at least nine points in the streamwise direction and 12 points in the wall-normal direction.

Figure 1. Computational domain and simulation set-up for the DNS case M6Tw025. The reference length
![]() $\unicode[STIX]{x1D6FF}_{i}$
is the thickness of the boundary layer (based on
$\unicode[STIX]{x1D6FF}_{i}$
is the thickness of the boundary layer (based on
![]() $99\,\%$
of the free-stream velocity) at the inlet plane. An instantaneous flow is shown in the domain, visualized by the isosurface of the magnitude of the density gradient,
$99\,\%$
of the free-stream velocity) at the inlet plane. An instantaneous flow is shown in the domain, visualized by the isosurface of the magnitude of the density gradient,
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\unicode[STIX]{x1D6FF}_{i}/\unicode[STIX]{x1D70C}_{\infty }=0.98$
, coloured by the streamwise velocity component (with levels from 0 to
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\unicode[STIX]{x1D6FF}_{i}/\unicode[STIX]{x1D70C}_{\infty }=0.98$
, coloured by the streamwise velocity component (with levels from 0 to
![]() $U_{\infty }$
, blue to red). Here,
$U_{\infty }$
, blue to red). Here,
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
are the streamwise, spanwise and wall-normal coordinates respectively.
$z$
are the streamwise, spanwise and wall-normal coordinates respectively.
Table 3. Grid resolution and domain size for case M6Tw025. Here,
![]() $L_{x}$
,
$L_{x}$
,
![]() $L_{y}$
and
$L_{y}$
and
![]() $L_{z}$
represent the domain size in the streamwise, spanwise and wall-normal directions respectively. The viscous length scale
$L_{z}$
represent the domain size in the streamwise, spanwise and wall-normal directions respectively. The viscous length scale
![]() $z_{\unicode[STIX]{x1D70F}}=8.0~\unicode[STIX]{x03BC}$
m corresponds to
$z_{\unicode[STIX]{x1D70F}}=8.0~\unicode[STIX]{x03BC}$
m corresponds to
![]() $x_{a}/\unicode[STIX]{x1D6FF}_{i}=88.6$
. The terms
$x_{a}/\unicode[STIX]{x1D6FF}_{i}=88.6$
. The terms
![]() $\unicode[STIX]{x0394}z_{min}^{+}$
and
$\unicode[STIX]{x0394}z_{min}^{+}$
and
![]() $\unicode[STIX]{x0394}z_{max}^{+}$
are the minimum and maximum wall-normal grid spacings for
$\unicode[STIX]{x0394}z_{max}^{+}$
are the minimum and maximum wall-normal grid spacings for
![]() $0\leqslant z/\unicode[STIX]{x1D6FF}_{i}\leqslant 8$
;
$0\leqslant z/\unicode[STIX]{x1D6FF}_{i}\leqslant 8$
;
![]() $\unicode[STIX]{x1D6FF}_{i}=1.33$
mm.
$\unicode[STIX]{x1D6FF}_{i}=1.33$
mm.
In the following sections, averages are first calculated over a streamwise window (
![]() $[x_{a}-0.5\unicode[STIX]{x1D6FF}_{i},x_{a}+0.5\unicode[STIX]{x1D6FF}_{i}]$
, with
$[x_{a}-0.5\unicode[STIX]{x1D6FF}_{i},x_{a}+0.5\unicode[STIX]{x1D6FF}_{i}]$
, with
![]() $x_{a}=88.6\unicode[STIX]{x1D6FF}_{i}$
, for case M6Tw025 and
$x_{a}=88.6\unicode[STIX]{x1D6FF}_{i}$
, for case M6Tw025 and
![]() $[x_{a}-0.9\unicode[STIX]{x1D6FF}_{i},x_{a}+0.9\unicode[STIX]{x1D6FF}_{i}]$
, with
$[x_{a}-0.9\unicode[STIX]{x1D6FF}_{i},x_{a}+0.9\unicode[STIX]{x1D6FF}_{i}]$
, with
![]() $x_{a}=54.1\unicode[STIX]{x1D6FF}_{i}$
, for case M6Tw076) and the spanwise direction for each instantaneous flow field; then, an ensemble average over
$x_{a}=54.1\unicode[STIX]{x1D6FF}_{i}$
, for case M6Tw076) and the spanwise direction for each instantaneous flow field; then, an ensemble average over
![]() $312$
flow-field snapshots (corresponding to
$312$
flow-field snapshots (corresponding to
![]() $\unicode[STIX]{x1D6FF}_{i}/U_{\infty }\approx 1016$
or
$\unicode[STIX]{x1D6FF}_{i}/U_{\infty }\approx 1016$
or
![]() $\unicode[STIX]{x1D6FF}/u_{\unicode[STIX]{x1D70F}}\approx 14.6$
) and over
$\unicode[STIX]{x1D6FF}/u_{\unicode[STIX]{x1D70F}}\approx 14.6$
) and over
![]() $153$
flow-field snapshots (corresponding to
$153$
flow-field snapshots (corresponding to
![]() $\unicode[STIX]{x1D6FF}_{i}/U_{\infty }\approx 240$
or
$\unicode[STIX]{x1D6FF}_{i}/U_{\infty }\approx 240$
or
![]() $\unicode[STIX]{x1D6FF}/u_{\unicode[STIX]{x1D70F}}\approx 7.2$
) is calculated for cases M6Tw025 and M6Tw076 respectively. A smaller number of flow-field snapshots was sufficient for case M6Tw076 because of the larger spanwise domain size (
$\unicode[STIX]{x1D6FF}/u_{\unicode[STIX]{x1D70F}}\approx 7.2$
) is calculated for cases M6Tw025 and M6Tw076 respectively. A smaller number of flow-field snapshots was sufficient for case M6Tw076 because of the larger spanwise domain size (
![]() $L_{y}/\unicode[STIX]{x1D6FF}_{i}=15.7$
) for this case compared with that for case M6Tw025 (
$L_{y}/\unicode[STIX]{x1D6FF}_{i}=15.7$
) for this case compared with that for case M6Tw025 (
![]() $L_{y}/\unicode[STIX]{x1D6FF}_{i}=8.8$
). The effect of spanwise domain size on flow statistics is monitored by comparing case M6Tw076 with an auxiliary simulation of the same grid resolution but with a narrower span of
$L_{y}/\unicode[STIX]{x1D6FF}_{i}=8.8$
). The effect of spanwise domain size on flow statistics is monitored by comparing case M6Tw076 with an auxiliary simulation of the same grid resolution but with a narrower span of
![]() $L_{y}/\unicode[STIX]{x1D6FF}_{i}=6.26$
, and negligible difference is observed in the flow statistics of interest. The outflow boundary condition has no influence on boundary-layer profiles within the selected streamwise window over which averages are calculated. Statistical convergence for both cases is verified by calculating averages over varying streamwise window sizes or over a different number of snapshots and by making sure that the differences in flow statistics are negligible (
$L_{y}/\unicode[STIX]{x1D6FF}_{i}=6.26$
, and negligible difference is observed in the flow statistics of interest. The outflow boundary condition has no influence on boundary-layer profiles within the selected streamwise window over which averages are calculated. Statistical convergence for both cases is verified by calculating averages over varying streamwise window sizes or over a different number of snapshots and by making sure that the differences in flow statistics are negligible (
![]() ${<}1\,\%$
) among the different data-averaging techniques. Data for free-stream acoustic radiation were not sampled at the same value of
${<}1\,\%$
) among the different data-averaging techniques. Data for free-stream acoustic radiation were not sampled at the same value of
![]() $z/\unicode[STIX]{x1D6FF}$
for the two cases. Therefore, comparison of statistical and spectral characteristics will be made between predictions at
$z/\unicode[STIX]{x1D6FF}$
for the two cases. Therefore, comparison of statistical and spectral characteristics will be made between predictions at
![]() $z/\unicode[STIX]{x1D6FF}=2.36$
(i.e.
$z/\unicode[STIX]{x1D6FF}=2.36$
(i.e.
![]() $z_{\infty }=2.36\unicode[STIX]{x1D6FF}$
) for case M6Tw025 and
$z_{\infty }=2.36\unicode[STIX]{x1D6FF}$
) for case M6Tw025 and
![]() $z/\unicode[STIX]{x1D6FF}=2.63$
(i.e.
$z/\unicode[STIX]{x1D6FF}=2.63$
(i.e.
![]() $z_{\infty }=2.63\unicode[STIX]{x1D6FF}$
) for case M6Tw076. Throughout the paper, standard (Reynolds) averages are denoted by an overbar,
$z_{\infty }=2.63\unicode[STIX]{x1D6FF}$
) for case M6Tw076. Throughout the paper, standard (Reynolds) averages are denoted by an overbar,
![]() $\overline{f}$
, and fluctuations around standard averages are denoted by a single prime, as
$\overline{f}$
, and fluctuations around standard averages are denoted by a single prime, as
![]() $f^{\prime }=f-\overline{f}$
. Negligible differences have been found between the standard and density-weighted (Favre) averages for the statistics reported in this article.
$f^{\prime }=f-\overline{f}$
. Negligible differences have been found between the standard and density-weighted (Favre) averages for the statistics reported in this article.
3 Assessment of DNS data
In this section, the first- and second-moment statistics of the velocity and temperature fields are reported at the selected downstream location (
![]() $x_{a}$
). The data are compared with published data, especially those of turbulent boundary layers in the hypersonic cold-wall regime.
$x_{a}$
). The data are compared with published data, especially those of turbulent boundary layers in the hypersonic cold-wall regime.
Figure 2(a) plots the van Driest transformed mean velocity
![]() $u_{VD}^{+}$
, which is defined as
$u_{VD}^{+}$
, which is defined as
The mean velocity shows an approximately logarithmic region where
![]() $u_{VD}^{+}=(1/k)\log (z^{+})+C$
upon van Driest transformation. Consistent with the published data by Duan et al. (Reference Duan, Beekman and Martín2010), Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015), Modesti & Pirozzoli (Reference Modesti and Pirozzoli2016) and Wu et al. (Reference Wu, Bi, Hussain and She2017), the van Driest-transformed mean velocity shows a shrinking of the linear viscous sublayer with higher wall cooling, while the additive constant
$u_{VD}^{+}=(1/k)\log (z^{+})+C$
upon van Driest transformation. Consistent with the published data by Duan et al. (Reference Duan, Beekman and Martín2010), Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015), Modesti & Pirozzoli (Reference Modesti and Pirozzoli2016) and Wu et al. (Reference Wu, Bi, Hussain and She2017), the van Driest-transformed mean velocity shows a shrinking of the linear viscous sublayer with higher wall cooling, while the additive constant
![]() $C$
in the log law does not seem to be significantly affected. Figure 2(b) shows a significantly better collapse of data in both the viscous sublayer and the log layer among the computational datasets involving different wall-cooling rates, after the mean velocity and the wall-normal coordinate are transformed according to the proposal by Trettel & Larsson (Reference Trettel and Larsson2016) as
$C$
in the log law does not seem to be significantly affected. Figure 2(b) shows a significantly better collapse of data in both the viscous sublayer and the log layer among the computational datasets involving different wall-cooling rates, after the mean velocity and the wall-normal coordinate are transformed according to the proposal by Trettel & Larsson (Reference Trettel and Larsson2016) as

Figure 2. Mean-velocity profiles transformed according to (a) van Driest and (b) Trettel & Larsson (Reference Trettel and Larsson2016). Symbols: △ (green), Duan et al. (Reference Duan, Beekman and Martín2010) M5T1,
![]() $M_{\infty }=5$
,
$M_{\infty }=5$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=798$
,
$Re_{\unicode[STIX]{x1D70F}}=798$
,
![]() $T_{w}/T_{r}=0.18$
; ▼, Duan et al. (Reference Duan, Beekman and Martín2010) M5T2,
$T_{w}/T_{r}=0.18$
; ▼, Duan et al. (Reference Duan, Beekman and Martín2010) M5T2,
![]() $M_{\infty }=5$
,
$M_{\infty }=5$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=386$
,
$Re_{\unicode[STIX]{x1D70F}}=386$
,
![]() $T_{w}/T_{r}=1.0$
; ◃, Modesti & Pirozzoli (Reference Modesti and Pirozzoli2016),
$T_{w}/T_{r}=1.0$
; ◃, Modesti & Pirozzoli (Reference Modesti and Pirozzoli2016),
![]() $M_{\infty }=1.9$
,
$M_{\infty }=1.9$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=448$
,
$Re_{\unicode[STIX]{x1D70F}}=448$
,
![]() $T_{w}/T_{r}=0.24$
; ♢ (violet red), Wu et al. (Reference Wu, Bi, Hussain and She2017),
$T_{w}/T_{r}=0.24$
; ♢ (violet red), Wu et al. (Reference Wu, Bi, Hussain and She2017),
![]() $M_{\infty }=4.5$
,
$M_{\infty }=4.5$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=2200$
,
$Re_{\unicode[STIX]{x1D70F}}=2200$
,
![]() $T_{w}/T_{r}=0.22$
; ○, Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015),
$T_{w}/T_{r}=0.22$
; ○, Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015),
![]() $M_{\infty }=2$
,
$M_{\infty }=2$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=507$
,
$Re_{\unicode[STIX]{x1D70F}}=507$
,
![]() $T_{w}/T_{r}=0.5$
.
$T_{w}/T_{r}=0.5$
.
Figure 3 plots the streamwise turbulence intensity and the Reynolds shear stress. A significantly improved collapse of data is achieved by Morkovin’s scaling (Morkovin Reference Morkovin and Favre1962), which takes into account the variation in mean flow properties. Morkovin’s scaling brings the magnitudes of the extrema in the compressible cases closer to the incompressible results of Schlatter & Örlü (Reference Schlatter and Örlü2010). The better collapse of data between cases M6Tw025 and M6Tw076 in figure 3(b) indicates that the effect of wall cooling on fluctuating velocity intensities can be largely accounted for by Morkovin’s scaling. Similarly improved collapse of data is achieved by Morkovin’s scaling for turbulence intensities in the spanwise and wall-normal directions.

Figure 3. Distribution of r.m.s. velocity components as a function of wall-normal distance. Curves and symbols: —— (red), M6Tw025,
![]() $M_{\infty }=5.86$
,
$M_{\infty }=5.86$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=450$
,
$Re_{\unicode[STIX]{x1D70F}}=450$
,
![]() $T_{w}/T_{r}=0.25$
; – ⋅ – ⋅ – (blue), M6Tw076,
$T_{w}/T_{r}=0.25$
; – ⋅ – ⋅ – (blue), M6Tw076,
![]() $M_{\infty }=5.86$
,
$M_{\infty }=5.86$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=453$
,
$Re_{\unicode[STIX]{x1D70F}}=453$
,
![]() $T_{w}/T_{r}=0.76$
; – – –, Duan et al. (Reference Duan, Beekman and Martín2010),
$T_{w}/T_{r}=0.76$
; – – –, Duan et al. (Reference Duan, Beekman and Martín2010),
![]() $M_{\infty }=5$
,
$M_{\infty }=5$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=798$
,
$Re_{\unicode[STIX]{x1D70F}}=798$
,
![]() $T_{w}/T_{r}=0.18$
; — ⋅ ⋅ —, Duan et al. (Reference Duan, Beekman and Martín2010),
$T_{w}/T_{r}=0.18$
; — ⋅ ⋅ —, Duan et al. (Reference Duan, Beekman and Martín2010),
![]() $M_{\infty }=5$
,
$M_{\infty }=5$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=386$
,
$Re_{\unicode[STIX]{x1D70F}}=386$
,
![]() $T_{w}/T_{r}=1.0$
; ◻, Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015),
$T_{w}/T_{r}=1.0$
; ◻, Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015),
![]() $M_{\infty }=2$
,
$M_{\infty }=2$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=507$
,
$Re_{\unicode[STIX]{x1D70F}}=507$
,
![]() $T_{w}/T_{r}=0.5$
; △ (violet red), Schlatter & Örlü (Reference Schlatter and Örlü2010),
$T_{w}/T_{r}=0.5$
; △ (violet red), Schlatter & Örlü (Reference Schlatter and Örlü2010),
![]() $M_{\infty }\approx 0$
,
$M_{\infty }\approx 0$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=500$
; ●, Peltier, Humble & Bowersox (Reference Peltier, Humble and Bowersox2016),
$Re_{\unicode[STIX]{x1D70F}}=500$
; ●, Peltier, Humble & Bowersox (Reference Peltier, Humble and Bowersox2016),
![]() $M_{\infty }=4.9$
,
$M_{\infty }=4.9$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=1100$
,
$Re_{\unicode[STIX]{x1D70F}}=1100$
,
![]() $T_{w}/T_{r}=0.9$
.
$T_{w}/T_{r}=0.9$
.

Figure 4. The coupling between thermal and velocity fields: (a) mean temperature–velocity relation; (b) DNS-predicted turbulent heat flux and the theoretical model of Bowersox (Reference Bowersox2009); (c) turbulent Prandtl number
![]() $Pr_{t}$
; (d) modified SRAs of Huang, Coleman & Bradshaw (Reference Huang, Coleman and Bradshaw1995) and Zhang et al. (Reference Zhang, Bi, Hussain and She2014). Curves and symbols: – – –, Duan et al. (Reference Duan, Beekman and Martín2010),
$Pr_{t}$
; (d) modified SRAs of Huang, Coleman & Bradshaw (Reference Huang, Coleman and Bradshaw1995) and Zhang et al. (Reference Zhang, Bi, Hussain and She2014). Curves and symbols: – – –, Duan et al. (Reference Duan, Beekman and Martín2010),
![]() $M_{\infty }=5$
,
$M_{\infty }=5$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=798$
,
$Re_{\unicode[STIX]{x1D70F}}=798$
,
![]() $T_{w}/T_{r}=0.18$
; — ⋅ ⋅ —, Duan et al. (Reference Duan, Beekman and Martín2010),
$T_{w}/T_{r}=0.18$
; — ⋅ ⋅ —, Duan et al. (Reference Duan, Beekman and Martín2010),
![]() $M_{\infty }=5$
,
$M_{\infty }=5$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=386$
,
$Re_{\unicode[STIX]{x1D70F}}=386$
,
![]() $T_{w}/T_{r}=1.0$
; ○, Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015),
$T_{w}/T_{r}=1.0$
; ○, Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015),
![]() $M_{\infty }=2$
,
$M_{\infty }=2$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=507$
,
$Re_{\unicode[STIX]{x1D70F}}=507$
,
![]() $T_{w}/T_{r}=0.5$
.
$T_{w}/T_{r}=0.5$
.
As far as the coupling between thermal and velocity fields is concerned, figure 4 plots several temperature–velocity scalings for high-speed turbulent boundary layers, including the mean temperature–velocity relation, the turbulent heat flux
![]() $\overline{\unicode[STIX]{x1D70C}}\overline{w^{\prime }T^{\prime }}$
, the turbulent Prandtl number
$\overline{\unicode[STIX]{x1D70C}}\overline{w^{\prime }T^{\prime }}$
, the turbulent Prandtl number
![]() $Pr_{t}\equiv (\overline{\unicode[STIX]{x1D70C}u^{\prime }w^{\prime }}(\unicode[STIX]{x2202}\overline{T}/\unicode[STIX]{x2202}z))/(\overline{\unicode[STIX]{x1D70C}w^{\prime }T^{\prime }}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}z))$
and the modified strong Reynolds analogies (SRAs) of Huang et al. (Reference Huang, Coleman and Bradshaw1995) and Zhang et al. (Reference Zhang, Bi, Hussain and She2014). The present spatial DNS results at Mach 6 are generally consistent with the predictions from several previous studies at lower Mach numbers (Duan et al.
Reference Duan, Beekman and Martín2010; Zhang et al.
Reference Zhang, Bi, Hussain and She2014; Shadloo et al.
Reference Shadloo, Hadjadj and Hussain2015) with regard to the wall-temperature dependence of the temperature–velocity scalings. In particular, figure 4(a) shows that strong wall cooling causes a deviation of the DNS from Walz’s relation (Walz Reference Walz1969), which is commonly used to relate the mean temperature and velocity as
$Pr_{t}\equiv (\overline{\unicode[STIX]{x1D70C}u^{\prime }w^{\prime }}(\unicode[STIX]{x2202}\overline{T}/\unicode[STIX]{x2202}z))/(\overline{\unicode[STIX]{x1D70C}w^{\prime }T^{\prime }}(\unicode[STIX]{x2202}\overline{u}/\unicode[STIX]{x2202}z))$
and the modified strong Reynolds analogies (SRAs) of Huang et al. (Reference Huang, Coleman and Bradshaw1995) and Zhang et al. (Reference Zhang, Bi, Hussain and She2014). The present spatial DNS results at Mach 6 are generally consistent with the predictions from several previous studies at lower Mach numbers (Duan et al.
Reference Duan, Beekman and Martín2010; Zhang et al.
Reference Zhang, Bi, Hussain and She2014; Shadloo et al.
Reference Shadloo, Hadjadj and Hussain2015) with regard to the wall-temperature dependence of the temperature–velocity scalings. In particular, figure 4(a) shows that strong wall cooling causes a deviation of the DNS from Walz’s relation (Walz Reference Walz1969), which is commonly used to relate the mean temperature and velocity as
A significantly improved comparison for the cold-wall case (case M6Tw025) is achieved by using the generalized Reynolds analogy of Zhang et al. (Reference Zhang, Bi, Hussain and She2014), in which a general recovery factor
![]() $r_{g}$
is introduced and
$r_{g}$
is introduced and
![]() $T_{r}$
in equation (3.3) is accordingly replaced by
$T_{r}$
in equation (3.3) is accordingly replaced by
![]() $T_{rg}$
as
$T_{rg}$
as
where
![]() $T_{rg}=T_{\infty }+r_{g}U_{\infty }^{2}/(2C_{p})$
with
$T_{rg}=T_{\infty }+r_{g}U_{\infty }^{2}/(2C_{p})$
with
![]() $r_{g}=2C_{p}(T_{w}-T_{\infty })/U_{\infty }^{2}-2Prq_{w}/(U_{\infty }\unicode[STIX]{x1D70F}_{w})$
, where
$r_{g}=2C_{p}(T_{w}-T_{\infty })/U_{\infty }^{2}-2Prq_{w}/(U_{\infty }\unicode[STIX]{x1D70F}_{w})$
, where
![]() $Pr$
is the molecular Prandtl number and
$Pr$
is the molecular Prandtl number and
![]() $C_{p}$
is the heat capacity at constant pressure. Equation (3.4) explicitly accounts for the wall heat flux
$C_{p}$
is the heat capacity at constant pressure. Equation (3.4) explicitly accounts for the wall heat flux
![]() $q_{w}$
, and it coincides with Walz’s relation in the case of adiabatic walls.
$q_{w}$
, and it coincides with Walz’s relation in the case of adiabatic walls.
Figure 4(b) shows that the DNS-predicted turbulent heat flux
![]() $\overline{\unicode[STIX]{x1D70C}}\overline{w^{\prime }T^{\prime }}$
compares well with the prediction of the theoretical model by Bowersox (Reference Bowersox2009), consistent with the finding by Poggie (Reference Poggie2015). The DNS-predicted turbulent Prandtl number compares well with the computations of Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015) and shows singular behaviour near the wall where the correlation
$\overline{\unicode[STIX]{x1D70C}}\overline{w^{\prime }T^{\prime }}$
compares well with the prediction of the theoretical model by Bowersox (Reference Bowersox2009), consistent with the finding by Poggie (Reference Poggie2015). The DNS-predicted turbulent Prandtl number compares well with the computations of Shadloo et al. (Reference Shadloo, Hadjadj and Hussain2015) and shows singular behaviour near the wall where the correlation
![]() $\overline{w^{\prime }T^{\prime }}$
is zero (figure 4
c). The SRA relates the temperature fluctuations
$\overline{w^{\prime }T^{\prime }}$
is zero (figure 4
c). The SRA relates the temperature fluctuations
![]() $T_{rms}^{\prime }$
to the streamwise velocity fluctuations
$T_{rms}^{\prime }$
to the streamwise velocity fluctuations
![]() $u_{rms}^{\prime }$
, as given by
$u_{rms}^{\prime }$
, as given by
where
![]() $a=Pr_{t}$
in Huang’s modified SRA (Huang et al.
Reference Huang, Coleman and Bradshaw1995) and
$a=Pr_{t}$
in Huang’s modified SRA (Huang et al.
Reference Huang, Coleman and Bradshaw1995) and
![]() $a=\overline{Pr_{t}}\equiv Pr_{t}(1+\bar{w}\overline{\unicode[STIX]{x1D70C}^{\prime }u^{\prime }}/\overline{\unicode[STIX]{x1D70C}u^{\prime }w^{\prime }})/(1+\bar{w}\overline{\unicode[STIX]{x1D70C}^{\prime }T^{\prime }}/\overline{\unicode[STIX]{x1D70C}w^{\prime }T^{\prime }})$
in Zhang’s version of the modified SRA (Zhang et al.
Reference Zhang, Bi, Hussain and She2014), and
$a=\overline{Pr_{t}}\equiv Pr_{t}(1+\bar{w}\overline{\unicode[STIX]{x1D70C}^{\prime }u^{\prime }}/\overline{\unicode[STIX]{x1D70C}u^{\prime }w^{\prime }})/(1+\bar{w}\overline{\unicode[STIX]{x1D70C}^{\prime }T^{\prime }}/\overline{\unicode[STIX]{x1D70C}w^{\prime }T^{\prime }})$
in Zhang’s version of the modified SRA (Zhang et al.
Reference Zhang, Bi, Hussain and She2014), and
![]() $M=\overline{u}/\sqrt{\unicode[STIX]{x1D6FE}R\overline{T}}$
is the local Mach number. Figure 4(d) shows that the modified SRA of Zhang et al. (Reference Zhang, Bi, Hussain and She2014) gives a slightly improved prediction between
$M=\overline{u}/\sqrt{\unicode[STIX]{x1D6FE}R\overline{T}}$
is the local Mach number. Figure 4(d) shows that the modified SRA of Zhang et al. (Reference Zhang, Bi, Hussain and She2014) gives a slightly improved prediction between
![]() $u_{rms}^{\prime }$
and
$u_{rms}^{\prime }$
and
![]() $T_{rms}^{\prime }$
than that of Huang et al. (Reference Huang, Coleman and Bradshaw1995).
$T_{rms}^{\prime }$
than that of Huang et al. (Reference Huang, Coleman and Bradshaw1995).
4 Boundary-layer-induced pressure fluctuations
In this section, the statistical and spectral characteristics of pressure fluctuations induced by hypersonic cold-wall turbulent boundary layers are discussed, highlighting their dependence on the wall temperature. The pressure statistics analysed include the fluctuation intensity, frequency power spectral density, space–time correlations and propagation speed.
The frequency spectrum of the pressure fluctuations is defined as
where the overbar indicates an average over the local streamwise window, the spanwise (
![]() $y$
) direction and the time (
$y$
) direction and the time (
![]() $t$
). Power spectra for case M6Tw025 are calculated using the Welch method (Welch Reference Welch1967) with 12 segments and
$t$
). Power spectra for case M6Tw025 are calculated using the Welch method (Welch Reference Welch1967) with 12 segments and
![]() $50\,\%$
overlap. A Hanning window is used for weighting the data prior to the fast Fourier transform processing. The sampling frequency is approximately
$50\,\%$
overlap. A Hanning window is used for weighting the data prior to the fast Fourier transform processing. The sampling frequency is approximately
![]() $31~U_{\infty }/\unicode[STIX]{x1D6FF}_{i}$
(corresponding to 20 MHz), and the length of an individual segment is approximately
$31~U_{\infty }/\unicode[STIX]{x1D6FF}_{i}$
(corresponding to 20 MHz), and the length of an individual segment is approximately
![]() $156~\unicode[STIX]{x1D6FF}_{i}/U_{\infty }$
for case M6Tw025. The calculation of power spectra for case M6Tw076 follows that described in Duan et al. (Reference Duan, Choudhari and Zhang2016). For both cases, the power spectra do not change upon changing the window function between Hanning and Hamming windows (at least in the reported frequency ranges), and negligible differences are found when the number of data segments is varied from eight to 12.
$156~\unicode[STIX]{x1D6FF}_{i}/U_{\infty }$
for case M6Tw025. The calculation of power spectra for case M6Tw076 follows that described in Duan et al. (Reference Duan, Choudhari and Zhang2016). For both cases, the power spectra do not change upon changing the window function between Hanning and Hamming windows (at least in the reported frequency ranges), and negligible differences are found when the number of data segments is varied from eight to 12.
The two-point space–time correlation coefficient of the pressure field is defined as
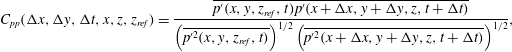 $$\begin{eqnarray}C_{pp}(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y,\unicode[STIX]{x0394}t,x,z,z_{ref})=\frac{\overline{p^{\prime }(x,y,z_{ref},t)p^{\prime }(x+\unicode[STIX]{x0394}x,y+\unicode[STIX]{x0394}y,z,t+\unicode[STIX]{x0394}t)}}{\left(\overline{{p^{\prime }}^{2}(x,y,z_{ref},t)}\right)^{1/2}\left(\overline{{p^{\prime }}^{2}(x+\unicode[STIX]{x0394}x,y+\unicode[STIX]{x0394}y,z,t+\unicode[STIX]{x0394}t)}\right)^{1/2}},\end{eqnarray}$$
$$\begin{eqnarray}C_{pp}(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y,\unicode[STIX]{x0394}t,x,z,z_{ref})=\frac{\overline{p^{\prime }(x,y,z_{ref},t)p^{\prime }(x+\unicode[STIX]{x0394}x,y+\unicode[STIX]{x0394}y,z,t+\unicode[STIX]{x0394}t)}}{\left(\overline{{p^{\prime }}^{2}(x,y,z_{ref},t)}\right)^{1/2}\left(\overline{{p^{\prime }}^{2}(x+\unicode[STIX]{x0394}x,y+\unicode[STIX]{x0394}y,z,t+\unicode[STIX]{x0394}t)}\right)^{1/2}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x0394}x$
and
$\unicode[STIX]{x0394}x$
and
![]() $\unicode[STIX]{x0394}y$
are the spatial separations in the streamwise and spanwise directions respectively,
$\unicode[STIX]{x0394}y$
are the spatial separations in the streamwise and spanwise directions respectively,
![]() $\unicode[STIX]{x0394}t$
is the time delay and
$\unicode[STIX]{x0394}t$
is the time delay and
![]() $z_{ref}$
is the wall-normal location at which the correlation is computed.
$z_{ref}$
is the wall-normal location at which the correlation is computed.
4.1 Root mean square of pressure fluctuations
In this section, the wall-normal variation of pressure statistics for the cold-wall hypersonic turbulent boundary layer (case M6Tw025) is discussed. The results are compared with turbulent boundary layers with an adiabatic or nearly adiabatic wall to highlight the effect of wall cooling.
Figures 5(a) and 5(b) show the profiles of the r.m.s. of pressure fluctuations
![]() $p_{rms}^{\prime }$
normalized by the local wall shear stress
$p_{rms}^{\prime }$
normalized by the local wall shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
. For case M6Tw025,
$\unicode[STIX]{x1D70F}_{w}$
. For case M6Tw025,
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
undergoes a rapid increase in magnitude as
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
undergoes a rapid increase in magnitude as
![]() $z\rightarrow 0$
, with
$z\rightarrow 0$
, with
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}\approx 3.5$
at the wall and
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}\approx 3.5$
at the wall and
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}\approx 2.2$
at
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}\approx 2.2$
at
![]() $z/\unicode[STIX]{x1D6FF}\approx 0.08$
. The magnitude of pressure fluctuation nearly plateaus for
$z/\unicode[STIX]{x1D6FF}\approx 0.08$
. The magnitude of pressure fluctuation nearly plateaus for
![]() $0.08\lessapprox z/\unicode[STIX]{x1D6FF}\lessapprox 0.2$
. For case M6Tw076 and the DNS results of Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011), however, a similarly rapid increase in the magnitude of pressure fluctuation with respect to
$0.08\lessapprox z/\unicode[STIX]{x1D6FF}\lessapprox 0.2$
. For case M6Tw076 and the DNS results of Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011), however, a similarly rapid increase in the magnitude of pressure fluctuation with respect to
![]() $\unicode[STIX]{x1D70F}_{w}$
as
$\unicode[STIX]{x1D70F}_{w}$
as
![]() $z\rightarrow 0$
is not observed. Instead, the maximum of
$z\rightarrow 0$
is not observed. Instead, the maximum of
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
is located away from the wall at
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
is located away from the wall at
![]() $z/\unicode[STIX]{x1D6FF}\approx 0.08$
(
$z/\unicode[STIX]{x1D6FF}\approx 0.08$
(
![]() $z^{+}\approx 25$
). The peak of
$z^{+}\approx 25$
). The peak of
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
is approximately 20 % lower in magnitude for case M6Tw076 than for case M6Tw025. The large difference in
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
is approximately 20 % lower in magnitude for case M6Tw076 than for case M6Tw025. The large difference in
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
values close to the wall between the turbulent boundary layer with a cold wall (case M6Tw025) and those with an adiabatic or nearly adiabatic wall (case M6Tw076 and that by Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011)) indicates a strong influence of wall cooling on the pressure fluctuations near the wall. The influence of wall cooling on
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
values close to the wall between the turbulent boundary layer with a cold wall (case M6Tw025) and those with an adiabatic or nearly adiabatic wall (case M6Tw076 and that by Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011)) indicates a strong influence of wall cooling on the pressure fluctuations near the wall. The influence of wall cooling on
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
becomes much weaker in the outer part of the boundary layer (
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
becomes much weaker in the outer part of the boundary layer (
![]() $z/\unicode[STIX]{x1D6FF}>0.3$
) and nearly vanishes in the free stream. Outside the boundary layer,
$z/\unicode[STIX]{x1D6FF}>0.3$
) and nearly vanishes in the free stream. Outside the boundary layer,
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
approaches a constant value of
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
approaches a constant value of
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}\approx 0.9$
for both the M6Tw025 and M6Tw076 cases. Figures 5(a) and 5(b) show the profiles of r.m.s. pressure fluctuations normalized by the local wall shear stress
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}\approx 0.9$
for both the M6Tw025 and M6Tw076 cases. Figures 5(a) and 5(b) show the profiles of r.m.s. pressure fluctuations normalized by the local wall shear stress
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
. Figures 5(c) and 5(d) further plot the profiles of r.m.s. pressure fluctuations
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
. Figures 5(c) and 5(d) further plot the profiles of r.m.s. pressure fluctuations
![]() $p_{rms}^{\prime }$
normalized by the local mean (static) pressure
$p_{rms}^{\prime }$
normalized by the local mean (static) pressure
![]() $\overline{p}$
and the free-stream dynamic pressure
$\overline{p}$
and the free-stream dynamic pressure
![]() $q_{\infty }=0.5\unicode[STIX]{x1D70C}_{\infty }U_{\infty }^{2}$
respectively. In contrast to the similar values of
$q_{\infty }=0.5\unicode[STIX]{x1D70C}_{\infty }U_{\infty }^{2}$
respectively. In contrast to the similar values of
![]() $p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
, significantly different values of
$p_{rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
, significantly different values of
![]() $p_{rms}^{\prime }/\overline{p}$
and
$p_{rms}^{\prime }/\overline{p}$
and
![]() $p_{rms}^{\prime }/q_{\infty }$
are shown throughout the boundary layer between cases M6Tw025 and M6Tw076, indicating that the mean shear stress
$p_{rms}^{\prime }/q_{\infty }$
are shown throughout the boundary layer between cases M6Tw025 and M6Tw076, indicating that the mean shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
is a better scaling for
$\unicode[STIX]{x1D70F}_{w}$
is a better scaling for
![]() $p_{rms}^{\prime }$
than the mean and dynamic pressures that account for the effect of wall cooling.
$p_{rms}^{\prime }$
than the mean and dynamic pressures that account for the effect of wall cooling.

Figure 5. Pressure-fluctuation r.m.s. profile
![]() $p_{rms}^{\prime }$
as a function of wall-normal distance normalized by (a,b) the local wall shear stress
$p_{rms}^{\prime }$
as a function of wall-normal distance normalized by (a,b) the local wall shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
, (c) the mean pressure
$\unicode[STIX]{x1D70F}_{w}$
, (c) the mean pressure
![]() $\overline{p}$
and (d) the dynamic pressure
$\overline{p}$
and (d) the dynamic pressure
![]() $q_{\infty }$
. Symbols: ♢, Duan et al. (Reference Duan, Choudhari and Wu2014),
$q_{\infty }$
. Symbols: ♢, Duan et al. (Reference Duan, Choudhari and Wu2014),
![]() $M_{\infty }=2.5$
,
$M_{\infty }=2.5$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=510$
,
$Re_{\unicode[STIX]{x1D70F}}=510$
,
![]() $T_{w}/T_{r}=1.0$
; ○, Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011),
$T_{w}/T_{r}=1.0$
; ○, Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011),
![]() $M_{\infty }=4$
,
$M_{\infty }=4$
,
![]() $Re_{\unicode[STIX]{x1D70F}}=506$
,
$Re_{\unicode[STIX]{x1D70F}}=506$
,
![]() $T_{w}/T_{r}=1.0$
.
$T_{w}/T_{r}=1.0$
.
4.2 Frequency spectra of pressure fluctuations
Figure 6 compares the wall-pressure spectra of cases M6Tw025 and M6Tw076. The spectra are normalized so that the area under each curve is equal to unity. For reference, straight lines with slopes of
![]() $2$
,
$2$
,
![]() $-1$
,
$-1$
,
![]() $-7/3$
and
$-7/3$
and
![]() $-5$
are also included to gauge the rate of spectral roll-off across relatively low, mid, mid-to-high overlap and high frequencies respectively, according to Bull (Reference Bull1996). The wall-pressure spectrum shows a strong wall-temperature dependence, especially in regions of mid frequencies (i.e.
$-5$
are also included to gauge the rate of spectral roll-off across relatively low, mid, mid-to-high overlap and high frequencies respectively, according to Bull (Reference Bull1996). The wall-pressure spectrum shows a strong wall-temperature dependence, especially in regions of mid frequencies (i.e.
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }>0.03$
and
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }>0.03$
and
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}^{2}<0.3$
) and mid-to-high overlap frequencies (i.e.
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}^{2}<0.3$
) and mid-to-high overlap frequencies (i.e.
![]() $0.3<\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}^{2}<1$
), and neither the outer scaling (figure 6
a) nor the inner scaling (figure 6
b) collapses the spectrum between the two DNS cases. Given that the pressure spectrum at mid frequencies is typically attributed to convected turbulence in the logarithmic region and that at mid-to-high overlap frequencies is attributed to eddies in the highest part of the buffer region (
$0.3<\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}^{2}<1$
), and neither the outer scaling (figure 6
a) nor the inner scaling (figure 6
b) collapses the spectrum between the two DNS cases. Given that the pressure spectrum at mid frequencies is typically attributed to convected turbulence in the logarithmic region and that at mid-to-high overlap frequencies is attributed to eddies in the highest part of the buffer region (
![]() $20<z^{+}<30$
) (Bull Reference Bull1996), the large variation in the wall-pressure spectrum at mid and mid-to-high overlap frequencies with wall cooling is consistent with the large changes in eddies in buffer and log layers, as reflected by the differences in r.m.s. pressure values in figure 5. The deviation from Kolmogorov’s
$20<z^{+}<30$
) (Bull Reference Bull1996), the large variation in the wall-pressure spectrum at mid and mid-to-high overlap frequencies with wall cooling is consistent with the large changes in eddies in buffer and log layers, as reflected by the differences in r.m.s. pressure values in figure 5. The deviation from Kolmogorov’s
![]() $-7/3$
scaling in the overlap region between mid and high frequencies is consistent with the findings of Tsuji et al. (Reference Tsuji, Fransson, Alferdsson and Johansson2007) and Bernardini, Pirozzoli & Grasso (Reference Bernardini, Pirozzoli and Grasso2011). At both wall temperatures, the wall-pressure spectrum shows a rather weak frequency dependence at the lowest computed frequencies and exhibits the
$-7/3$
scaling in the overlap region between mid and high frequencies is consistent with the findings of Tsuji et al. (Reference Tsuji, Fransson, Alferdsson and Johansson2007) and Bernardini, Pirozzoli & Grasso (Reference Bernardini, Pirozzoli and Grasso2011). At both wall temperatures, the wall-pressure spectrum shows a rather weak frequency dependence at the lowest computed frequencies and exhibits the
![]() $\unicode[STIX]{x1D714}^{-5}$
scaling predicted theoretically by Blake (Reference Blake1986) at the highest computed frequencies. The premultiplied wall-pressure spectrum for case M6Tw025 (figure 6
c,d) consists of a sharper peak with a faster roll-off at both high and low frequencies compared with case M6Tw076, and wall cooling causes an increase in the dominant frequency from
$\unicode[STIX]{x1D714}^{-5}$
scaling predicted theoretically by Blake (Reference Blake1986) at the highest computed frequencies. The premultiplied wall-pressure spectrum for case M6Tw025 (figure 6
c,d) consists of a sharper peak with a faster roll-off at both high and low frequencies compared with case M6Tw076, and wall cooling causes an increase in the dominant frequency from
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }\approx 4$
(
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }\approx 4$
(
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}^{2}=0.4$
or
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}^{2}=0.4$
or
![]() $f\unicode[STIX]{x1D6FF}/U_{\infty }=1.2$
) for case M6Tw076 to
$f\unicode[STIX]{x1D6FF}/U_{\infty }=1.2$
) for case M6Tw076 to
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }\approx 5$
(
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }\approx 5$
(
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}^{2}=0.6$
or
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}^{2}=0.6$
or
![]() $f\unicode[STIX]{x1D6FF}/U_{\infty }=1.7$
) for case M6Tw025.
$f\unicode[STIX]{x1D6FF}/U_{\infty }=1.7$
) for case M6Tw025.

Figure 6. Comparison of pressure spectra at the wall (
![]() $z=0$
) between cases M6Tw025 and M6Tw076. The pressure spectrum is normalized so that the area under each curve is equal to unity. (a) Log–log plot in outer scale; (b) log–log plot in inner scale; (c) log–linear plot in outer scale; (d) log–linear plot in inner scale. The area under each curve is equal to unity. The value of
$z=0$
) between cases M6Tw025 and M6Tw076. The pressure spectrum is normalized so that the area under each curve is equal to unity. (a) Log–log plot in outer scale; (b) log–log plot in inner scale; (c) log–linear plot in outer scale; (d) log–linear plot in inner scale. The area under each curve is equal to unity. The value of
![]() $p_{rms}^{\prime }$
at the wall is
$p_{rms}^{\prime }$
at the wall is
![]() $100.8$
Pa for case M6Tw025 and
$100.8$
Pa for case M6Tw025 and
![]() $44.3$
Pa for case M6Tw076.
$44.3$
Pa for case M6Tw076.
Regarding the free-stream pressure spectra, figure 7(a) shows that the low-frequency range of the pressure spectra
![]() $\unicode[STIX]{x1D6F7}_{p}$
is relatively insensitive to
$\unicode[STIX]{x1D6F7}_{p}$
is relatively insensitive to
![]() $T_{w}/T_{r}$
when expressed in outer variables, and figure 7(b) shows that the high-frequency portions nearly overlap in inner variables, which conforms to the findings of the wall-pressure spectrum in low-speed adiabatic flows (Bull Reference Bull1996). Moreover, figures 7(c) and 7(d) show that the peak of the premultiplied spectrum is centred at a frequency of
$T_{w}/T_{r}$
when expressed in outer variables, and figure 7(b) shows that the high-frequency portions nearly overlap in inner variables, which conforms to the findings of the wall-pressure spectrum in low-speed adiabatic flows (Bull Reference Bull1996). Moreover, figures 7(c) and 7(d) show that the peak of the premultiplied spectrum is centred at a frequency of
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }\approx 1.5$
, which is more than three times lower than that of the pressure spectrum at the wall, indicating that the characteristic frequency of the acoustic mode is significantly lower than that of the vortical fluctuation close to the surface. The dominant frequency of the free-stream pressure spectrum is independent of wall temperature, indicating relatively insignificant influence of wall cooling on the free-stream pressure spectrum.
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}^{\ast }/U_{\infty }\approx 1.5$
, which is more than three times lower than that of the pressure spectrum at the wall, indicating that the characteristic frequency of the acoustic mode is significantly lower than that of the vortical fluctuation close to the surface. The dominant frequency of the free-stream pressure spectrum is independent of wall temperature, indicating relatively insignificant influence of wall cooling on the free-stream pressure spectrum.

Figure 7. Comparison of pressure spectra in the free stream (
![]() $z=z_{\infty }$
) between cases M6Tw025 and M6Tw076: (a) log–log plot in outer scale; (b) log–log plot in inner scale; (c) log–linear plot in outer scale; (d) log–linear plot in inner scale. The area under each curve is equal to unity. The value of
$z=z_{\infty }$
) between cases M6Tw025 and M6Tw076: (a) log–log plot in outer scale; (b) log–log plot in inner scale; (c) log–linear plot in outer scale; (d) log–linear plot in inner scale. The area under each curve is equal to unity. The value of
![]() $p_{rms}^{\prime }$
in the free stream is 24.8 Pa for case M6Tw025 and
$p_{rms}^{\prime }$
in the free stream is 24.8 Pa for case M6Tw025 and
![]() $13.9$
Pa for case M6Tw076.
$13.9$
Pa for case M6Tw076.

Figure 8. Three-dimensional representation of the spatial correlation coefficient
![]() $C_{pp}(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y,0,x_{a},z,z_{ref})$
of the pressure signal at multiple wall-normal locations for case M6Tw025. The flow goes from left to right towards the positive
$C_{pp}(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y,0,x_{a},z,z_{ref})$
of the pressure signal at multiple wall-normal locations for case M6Tw025. The flow goes from left to right towards the positive
![]() $x$
direction. Three-dimensional isosurfaces are shown at
$x$
direction. Three-dimensional isosurfaces are shown at
![]() $C_{pp}=0.1$
(blue) and
$C_{pp}=0.1$
(blue) and
![]() $0.6$
(green). In the horizontal planes going through the correlation origin (
$0.6$
(green). In the horizontal planes going through the correlation origin (
![]() $z=z_{ref}$
), the contour lines shown in white range from
$z=z_{ref}$
), the contour lines shown in white range from
![]() $0.1$
to
$0.1$
to
![]() $0.9$
.
$0.9$
.
4.3 Spatial correlation of pressure fluctuations
To illustrate the spatial size and orientation of statistically significant three-dimensional (3D) pressure structures, figure 8 plots the 3D correlation coefficient of the pressure signal
![]() $C_{pp}(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y,0,x_{a},z,z_{ref})$
as a function of wall-normal distance. For each reference height
$C_{pp}(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y,0,x_{a},z,z_{ref})$
as a function of wall-normal distance. For each reference height
![]() $z_{ref}$
, there exists a downward-leaning pressure structure with finite spatial size and an inclined orientation. The pressure structure has a spatial length scale of the order of the boundary-layer thickness
$z_{ref}$
, there exists a downward-leaning pressure structure with finite spatial size and an inclined orientation. The pressure structure has a spatial length scale of the order of the boundary-layer thickness
![]() $O(\unicode[STIX]{x1D6FF})$
in each direction and increases in size as the distance from the wall increases. The pressure structure is approximately perpendicular to the direction of
$O(\unicode[STIX]{x1D6FF})$
in each direction and increases in size as the distance from the wall increases. The pressure structure is approximately perpendicular to the direction of
![]() $U_{\infty }$
at the wall and becomes increasingly more downward leaning as it moves away from the wall in the inner and outer regions of the boundary layer. In the free stream, the inclination angle with respect to the direction of
$U_{\infty }$
at the wall and becomes increasingly more downward leaning as it moves away from the wall in the inner and outer regions of the boundary layer. In the free stream, the inclination angle with respect to the direction of
![]() $U_{\infty }$
approaches
$U_{\infty }$
approaches
![]() $\unicode[STIX]{x1D703}_{xz}\approx 28^{\circ }$
. The free-stream wave-front orientation closely matches the wave-front orientation of the instantaneous acoustic radiation visualized by numerical schlieren image, as will be shown in figure 9. Consistent with the spatial correlation in the free-stream region (figure 8
d), the 3D visualization in figure 9 shows that the free-stream pressure waves deviate from purely planar behaviour in the spanwise wall-normal (
$\unicode[STIX]{x1D703}_{xz}\approx 28^{\circ }$
. The free-stream wave-front orientation closely matches the wave-front orientation of the instantaneous acoustic radiation visualized by numerical schlieren image, as will be shown in figure 9. Consistent with the spatial correlation in the free-stream region (figure 8
d), the 3D visualization in figure 9 shows that the free-stream pressure waves deviate from purely planar behaviour in the spanwise wall-normal (
![]() $y$
–
$y$
–
![]() $z$
) plane and exhibit a preferred orientation of
$z$
) plane and exhibit a preferred orientation of
![]() $\unicode[STIX]{x1D703}\approx 28^{\circ }$
in the streamwise wall-normal (
$\unicode[STIX]{x1D703}\approx 28^{\circ }$
in the streamwise wall-normal (
![]() $x$
–
$x$
–
![]() $z$
) plane. The finite spanwise extent of the free-stream pressure waves is consistent with the finite size of acoustic sources that are responsible for generating the waves. Similar patterns of free-stream acoustic radiation are also found for case M6Tw076 (Duan et al.
Reference Duan, Choudhari and Zhang2016).
$z$
) plane. The finite spanwise extent of the free-stream pressure waves is consistent with the finite size of acoustic sources that are responsible for generating the waves. Similar patterns of free-stream acoustic radiation are also found for case M6Tw076 (Duan et al.
Reference Duan, Choudhari and Zhang2016).
Figure 10 compares the spatial correlation coefficient (with zero spanwise separation,
![]() $\unicode[STIX]{x0394}y=0$
) in the streamwise wall-normal plane between cases M6Tw025 and M6Tw076. At the wall (
$\unicode[STIX]{x0394}y=0$
) in the streamwise wall-normal plane between cases M6Tw025 and M6Tw076. At the wall (
![]() $z_{ref}/\unicode[STIX]{x1D6FF}=0$
), the pressure structures have a similar inclination angle of
$z_{ref}/\unicode[STIX]{x1D6FF}=0$
), the pressure structures have a similar inclination angle of
![]() $\unicode[STIX]{x1D703}_{xz}\approx 81^{\circ }$
for both cases. In the free stream, the structure angle for cases M6Tw025 and M6Tw076 decreases to
$\unicode[STIX]{x1D703}_{xz}\approx 81^{\circ }$
for both cases. In the free stream, the structure angle for cases M6Tw025 and M6Tw076 decreases to
![]() $\unicode[STIX]{x1D703}_{xz}\approx 28^{\circ }$
and
$\unicode[STIX]{x1D703}_{xz}\approx 28^{\circ }$
and
![]() $\unicode[STIX]{x1D703}_{xz}\approx 21^{\circ }$
respectively. The change in inclination might indicate that pressure disturbances generated within the boundary layer undergo less refraction before they are radiated to the free stream, resulting in a higher wave angle for case M6Tw025. The reduction in refraction for case M6Tw025 may be due to the less drastic variation in fluid properties (such as fluid density and temperature) because of wall cooling.
$\unicode[STIX]{x1D703}_{xz}\approx 21^{\circ }$
respectively. The change in inclination might indicate that pressure disturbances generated within the boundary layer undergo less refraction before they are radiated to the free stream, resulting in a higher wave angle for case M6Tw025. The reduction in refraction for case M6Tw025 may be due to the less drastic variation in fluid properties (such as fluid density and temperature) because of wall cooling.

Figure 9. Instantaneous flow visualization for case M6Tw025. The grey contours are those of numerical schlieren, with density gradient contour levels selected to emphasize disturbances in the free stream. The colour contours are those of the magnitude of vorticity, with contour levels selected to emphasize the large-scale motions within the boundary layer. The angle
![]() $\unicode[STIX]{x1D703}$
is between the flow direction and the acoustic wave front.
$\unicode[STIX]{x1D703}$
is between the flow direction and the acoustic wave front.

Figure 10. Contours of the spatial correlation coefficient of the pressure signal
![]() $C_{pp}(\unicode[STIX]{x0394}x,0,0,x_{a},z,z_{ref})$
in the streamwise wall-normal plane: (a)
$C_{pp}(\unicode[STIX]{x0394}x,0,0,x_{a},z,z_{ref})$
in the streamwise wall-normal plane: (a)
![]() $z_{ref}=0$
(wall); (b)
$z_{ref}=0$
(wall); (b)
![]() $z_{ref}=z_{\infty }$
(free stream); ——, M6Tw025; — ⋅ —, M6Tw076. Four contour levels are shown:
$z_{ref}=z_{\infty }$
(free stream); ——, M6Tw025; — ⋅ —, M6Tw076. Four contour levels are shown:
![]() $C_{pp}=0.1$
, 0.2, 0.4 and 0.8.
$C_{pp}=0.1$
, 0.2, 0.4 and 0.8.
4.4 Propagation and evolution of pressure structures
To quantify the overall propagation speed of pressure-carrying eddies or wavepackets as a function of distance from the wall, the bulk propagation speed is obtained as
This expression defines the bulk propagation speed
![]() $U_{b}$
by finding the value of
$U_{b}$
by finding the value of
![]() $U_{b}$
that minimizes the difference between the real time evolution of
$U_{b}$
that minimizes the difference between the real time evolution of
![]() $p(x,t)$
and a propagating frozen wave
$p(x,t)$
and a propagating frozen wave
![]() $p(x-U_{b}t)$
. A figure of merit for the frozen-wave approximation can be further defined as
$p(x-U_{b}t)$
. A figure of merit for the frozen-wave approximation can be further defined as
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{p}\equiv \frac{\left|\overline{(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}x)(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}t)}\right|}{\left[\overline{\left(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}t\right)^{2}}\;\overline{\left(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}x\right)^{2}}\right]^{1/2}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{p}\equiv \frac{\left|\overline{(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}x)(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}t)}\right|}{\left[\overline{\left(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}t\right)^{2}}\;\overline{\left(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}x\right)^{2}}\right]^{1/2}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FE}_{p}$
equals unity for a perfectly frozen wave and is zero for fast decaying or deforming waves as they convect downstream. This definition of the bulk propagation speed and figure of merit for the frozen-wave approximation was first used by Del Álamo & Jiménez (Reference Del Álamo and Jiménez2009) for the streamwise velocity fluctuations in turbulent channel flows.
$\unicode[STIX]{x1D6FE}_{p}$
equals unity for a perfectly frozen wave and is zero for fast decaying or deforming waves as they convect downstream. This definition of the bulk propagation speed and figure of merit for the frozen-wave approximation was first used by Del Álamo & Jiménez (Reference Del Álamo and Jiménez2009) for the streamwise velocity fluctuations in turbulent channel flows.
Figure 11 shows a comparison of the bulk propagation speed
![]() $U_{b}$
between cases M6Tw025 and M6Tw076. Wall cooling has a small influence on the propagation speed of pressure structures within the main part of the boundary layer and has nearly no influence on the propagation speed of radiated pressure waves in the free stream. Consistent with previous findings (Duan et al.
Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016), the free-stream propagation speed for case M6Tw025 is significantly lower than the mean velocity in the free stream.
$U_{b}$
between cases M6Tw025 and M6Tw076. Wall cooling has a small influence on the propagation speed of pressure structures within the main part of the boundary layer and has nearly no influence on the propagation speed of radiated pressure waves in the free stream. Consistent with previous findings (Duan et al.
Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016), the free-stream propagation speed for case M6Tw025 is significantly lower than the mean velocity in the free stream.
Figure 12 shows the wall-normal distribution of
![]() $\unicode[STIX]{x1D6FE}_{p}$
which provides a figure of merit for the frozen-wave approximation for cases M6Tw025 and M6Tw076. For both wall-temperature conditions,
$\unicode[STIX]{x1D6FE}_{p}$
which provides a figure of merit for the frozen-wave approximation for cases M6Tw025 and M6Tw076. For both wall-temperature conditions,
![]() $\unicode[STIX]{x1D6FE}_{p}$
is close to unity across the boundary layer, indicating that the propagation effect is overall more dominant than the evolution effect for the pressure structures. As the wall temperature decreases, the pressure structures become more ‘frozen’, with less significant evolution as they propagate downstream, especially for the pressure structures in the free stream.
$\unicode[STIX]{x1D6FE}_{p}$
is close to unity across the boundary layer, indicating that the propagation effect is overall more dominant than the evolution effect for the pressure structures. As the wall temperature decreases, the pressure structures become more ‘frozen’, with less significant evolution as they propagate downstream, especially for the pressure structures in the free stream.

Figure 11. Comparison of the bulk propagation speed of pressure fluctuations in (a) outer and (b) inner units between cases M6Tw025 and M6Tw076. Here,
![]() $U_{b}$
is defined based on (4.3).
$U_{b}$
is defined based on (4.3).

Figure 12. The distribution of the correlation coefficient
![]() $\unicode[STIX]{x1D6FE}_{p}$
which provides a figure of merit for the frozen-wave approximation. Here,
$\unicode[STIX]{x1D6FE}_{p}$
which provides a figure of merit for the frozen-wave approximation. Here,
![]() $\unicode[STIX]{x1D6FE}_{p}$
is defined based on (4.4).
$\unicode[STIX]{x1D6FE}_{p}$
is defined based on (4.4).

Figure 13. Contours of constant space–time correlation coefficient of the pressure signal
![]() $C_{pp}(\unicode[STIX]{x0394}x,0,\unicode[STIX]{x0394}t,x_{a},z_{ref},z_{ref})$
: (a) at the wall; (b) in the free stream; ——, M6Tw025; — ⋅ —, M6Tw076. Four contour levels are shown:
$C_{pp}(\unicode[STIX]{x0394}x,0,\unicode[STIX]{x0394}t,x_{a},z_{ref},z_{ref})$
: (a) at the wall; (b) in the free stream; ——, M6Tw025; — ⋅ —, M6Tw076. Four contour levels are shown:
![]() $C_{pp}=0.1$
, 0.2, 0.4 and 0.8.
$C_{pp}=0.1$
, 0.2, 0.4 and 0.8.
The propagation and evolution of large-scale pressure structures can be further investigated via the space–time correlation contours of pressure fluctuations,
![]() $C_{pp}$
(
$C_{pp}$
(
![]() $\unicode[STIX]{x0394}x,0$
,
$\unicode[STIX]{x0394}x,0$
,
![]() $\unicode[STIX]{x0394}t,x_{a},z_{ref}$
,
$\unicode[STIX]{x0394}t,x_{a},z_{ref}$
,
![]() $z_{ref}$
). Figure 13 shows contours of constant space–time correlation
$z_{ref}$
). Figure 13 shows contours of constant space–time correlation
![]() $C_{pp}$
(
$C_{pp}$
(
![]() $\unicode[STIX]{x0394}x,0$
,
$\unicode[STIX]{x0394}x,0$
,
![]() $\unicode[STIX]{x0394}t$
,
$\unicode[STIX]{x0394}t$
,
![]() $x_{a},z_{ref}$
,
$x_{a},z_{ref}$
,
![]() $z_{ref}$
) at the wall (
$z_{ref}$
) at the wall (
![]() $z_{ref}=0$
) and in the free stream (
$z_{ref}=0$
) and in the free stream (
![]() $z_{ref}=z_{\infty }$
) for cases M6Tw025 and M6Tw076. The skewed shape of the contours at both locations indicates the propagative nature of the pressure field, which is characterized by downstream propagation of either the coherent pressure-carrying eddies within the boundary layer or the pressure wavepackets in the free stream. Based on the space–time correlation data, the speed of propagation of pressure fluctuations can be estimated as the ratio
$z_{ref}=z_{\infty }$
) for cases M6Tw025 and M6Tw076. The skewed shape of the contours at both locations indicates the propagative nature of the pressure field, which is characterized by downstream propagation of either the coherent pressure-carrying eddies within the boundary layer or the pressure wavepackets in the free stream. Based on the space–time correlation data, the speed of propagation of pressure fluctuations can be estimated as the ratio
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x0394}t$
for a given time delay
$\unicode[STIX]{x0394}x/\unicode[STIX]{x0394}t$
for a given time delay
![]() $\unicode[STIX]{x0394}t$
at the value of
$\unicode[STIX]{x0394}t$
at the value of
![]() $\unicode[STIX]{x0394}x$
where
$\unicode[STIX]{x0394}x$
where
or for a given streamwise separation
![]() $\unicode[STIX]{x0394}x$
at the value of
$\unicode[STIX]{x0394}x$
at the value of
![]() $\unicode[STIX]{x0394}t$
where
$\unicode[STIX]{x0394}t$
where
Figures 14(a) and 14(b) compare the variation of bulk propagation speed with the free-stream Mach number at the wall and in the free stream respectively with some existing experiments and simulations. In the figure,
![]() $U_{b1}$
is defined based on the space–time correlation coefficient, with (4.5) for the time delay
$U_{b1}$
is defined based on the space–time correlation coefficient, with (4.5) for the time delay
![]() $\unicode[STIX]{x0394}t$
or frequency (
$\unicode[STIX]{x0394}t$
or frequency (
![]() $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x0394}t$
) where the premultiplied frequency spectrum (figures 6 and 7) attains its maximum. In analogy,
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x0394}t$
) where the premultiplied frequency spectrum (figures 6 and 7) attains its maximum. In analogy,
![]() $U_{b2}$
is derived based on (4.6) for the streamwise separation
$U_{b2}$
is derived based on (4.6) for the streamwise separation
![]() $\unicode[STIX]{x0394}x$
or wavenumber (
$\unicode[STIX]{x0394}x$
or wavenumber (
![]() $k_{1}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x0394}x$
) where the premultiplied one-dimensional wavenumber spectrum attains its maximum. The value of
$k_{1}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x0394}x$
) where the premultiplied one-dimensional wavenumber spectrum attains its maximum. The value of
![]() $U_{b3}$
is computed using (4.3) by assuming a ‘frozen wave/eddy’. Consistent with figure 11, the propagation speed based on the space–time correlation coefficient is comparable between cases M6Tw025 and M6Tw076, indicating that wall cooling has only a small influence on the overall propagation speed of pressure structures away from the wall. The Mach-number dependence of the bulk propagation speed is consistent with the previous data reported by Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011) for
$U_{b3}$
is computed using (4.3) by assuming a ‘frozen wave/eddy’. Consistent with figure 11, the propagation speed based on the space–time correlation coefficient is comparable between cases M6Tw025 and M6Tw076, indicating that wall cooling has only a small influence on the overall propagation speed of pressure structures away from the wall. The Mach-number dependence of the bulk propagation speed is consistent with the previous data reported by Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011) for
![]() $U_{b}$
at the wall and by Laufer (Reference Laufer1964) and Duan et al. (Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016) for
$U_{b}$
at the wall and by Laufer (Reference Laufer1964) and Duan et al. (Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016) for
![]() $U_{b}$
in the free stream.
$U_{b}$
in the free stream.

Figure 14. Bulk propagation speeds of the pressure fluctuation as a function of free-stream Mach number: (a) at the wall (
![]() $z_{ref}=0$
); (b) in the free stream (
$z_{ref}=0$
); (b) in the free stream (
![]() $z_{ref}=z_{\infty }$
). Symbols: squares, Kistler & Chen (Reference Kistler and Chen1963); left triangles, Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011); diamonds, Laufer (Reference Laufer1964); letters A, B, C, Duan et al. (Reference Duan, Choudhari and Wu2014); up triangle, circle, down triangle, case M6Tw025; letters D, E, F, case M6Tw076. Here,
$z_{ref}=z_{\infty }$
). Symbols: squares, Kistler & Chen (Reference Kistler and Chen1963); left triangles, Bernardini & Pirozzoli (Reference Bernardini and Pirozzoli2011); diamonds, Laufer (Reference Laufer1964); letters A, B, C, Duan et al. (Reference Duan, Choudhari and Wu2014); up triangle, circle, down triangle, case M6Tw025; letters D, E, F, case M6Tw076. Here,
![]() $U_{b1}$
,
$U_{b1}$
,
![]() $U_{b2}$
and
$U_{b2}$
and
![]() $U_{b3}$
are defined based on (4.5), (4.6) and (4.3) respectively.
$U_{b3}$
are defined based on (4.5), (4.6) and (4.3) respectively.
To study the propagation speed of spectral components of pressure fluctuations, the phase speed of pressure fluctuations is defined as
where
![]() $\unicode[STIX]{x0394}x$
is the distance between two pressure signals separated in the streamwise direction and
$\unicode[STIX]{x0394}x$
is the distance between two pressure signals separated in the streamwise direction and
![]() $\unicode[STIX]{x1D703}_{p}(\unicode[STIX]{x1D714})$
is the phase difference between the two streamwise-separated pressure signals derived based on the cross-spectrum of the two signals. In the current study, the streamwise separation
$\unicode[STIX]{x1D703}_{p}(\unicode[STIX]{x1D714})$
is the phase difference between the two streamwise-separated pressure signals derived based on the cross-spectrum of the two signals. In the current study, the streamwise separation
![]() $\unicode[STIX]{x0394}x$
is chosen to be the smallest streamwise distance at which two pressure signals are spatially sampled (
$\unicode[STIX]{x0394}x$
is chosen to be the smallest streamwise distance at which two pressure signals are spatially sampled (
![]() $\unicode[STIX]{x0394}x^{+}=6.42$
and
$\unicode[STIX]{x0394}x^{+}=6.42$
and
![]() $28.9$
for cases M6Tw025 and M6Tw076 respectively). At the selected streamwise separation, the coherence between the two signals is close to unity and the definition (4.7) thus provides a ‘local’ measurement of the phase speed. This definition was first used by Stegen & Van Atta (Reference Stegen and Van Atta1970) to measure the local phase speed of the Fourier components of the longitudinal velocity fluctuations in grid turbulence with a small probe spacing. Figure 15 shows the phase speed of pressure fluctuations
$28.9$
for cases M6Tw025 and M6Tw076 respectively). At the selected streamwise separation, the coherence between the two signals is close to unity and the definition (4.7) thus provides a ‘local’ measurement of the phase speed. This definition was first used by Stegen & Van Atta (Reference Stegen and Van Atta1970) to measure the local phase speed of the Fourier components of the longitudinal velocity fluctuations in grid turbulence with a small probe spacing. Figure 15 shows the phase speed of pressure fluctuations
![]() $U_{p}(\unicode[STIX]{x1D714})$
at the wall and in the free stream. At the wall, the phase speed shows a weak frequency dependence for both cases, and the wall-pressure structures of all frequencies propagate with speeds similar to the local bulk propagation speed. In the free stream, while the phase speed of the dominant pressure structures is similar to the local bulk propagation speed, wall cooling slightly increases the free-stream phase speed at higher frequencies, and the high-frequency pressure structures propagate with a speed larger than the bulk propagation speed.
$U_{p}(\unicode[STIX]{x1D714})$
at the wall and in the free stream. At the wall, the phase speed shows a weak frequency dependence for both cases, and the wall-pressure structures of all frequencies propagate with speeds similar to the local bulk propagation speed. In the free stream, while the phase speed of the dominant pressure structures is similar to the local bulk propagation speed, wall cooling slightly increases the free-stream phase speed at higher frequencies, and the high-frequency pressure structures propagate with a speed larger than the bulk propagation speed.

Figure 15. Comparison of phase speed (a) at the wall and (b) in the free stream. The phase speed
![]() $U_{p}(\unicode[STIX]{x1D714})$
is defined based on equation (4.7). The vertical dashed line denotes the peak frequency
$U_{p}(\unicode[STIX]{x1D714})$
is defined based on equation (4.7). The vertical dashed line denotes the peak frequency
![]() $\unicode[STIX]{x1D714}_{pk}$
where the premultiplied frequency spectrum attains its maximum.
$\unicode[STIX]{x1D714}_{pk}$
where the premultiplied frequency spectrum attains its maximum.
To interpret the Lagrangian decorrelation length of the coherent pressure structures, Figure 16 compares the spatial decay of the maximum space–time correlation of pressure fluctuations,
![]() $(C_{pp})_{max}$
, at the wall and in the free stream for cases M6Tw025 and M6Tw076. The slower rate of spatial decay in
$(C_{pp})_{max}$
, at the wall and in the free stream for cases M6Tw025 and M6Tw076. The slower rate of spatial decay in
![]() $(C_{pp})_{max}$
for case M6Tw025 indicates that wall cooling de-energizes pressure structures, making them evolve less rapidly as they propagate downstream. Such a trend is consistent with the larger values of the ‘frozen-wave’ index
$(C_{pp})_{max}$
for case M6Tw025 indicates that wall cooling de-energizes pressure structures, making them evolve less rapidly as they propagate downstream. Such a trend is consistent with the larger values of the ‘frozen-wave’ index
![]() $\unicode[STIX]{x1D6FE}_{p}$
(figure 12) for case M6Tw025.
$\unicode[STIX]{x1D6FE}_{p}$
(figure 12) for case M6Tw025.

Figure 16. Comparison of the maximum space–time correlation coefficient of pressure fluctuations,
![]() $(C_{pp})_{max}$
, as a function of streamwise separation
$(C_{pp})_{max}$
, as a function of streamwise separation
![]() $\unicode[STIX]{x0394}x$
(a) at the wall and (b) in the free stream for cases M6Tw025 and M6Tw076.
$\unicode[STIX]{x0394}x$
(a) at the wall and (b) in the free stream for cases M6Tw025 and M6Tw076.
Table 4. The free-stream disturbance field for cases M6Tw025 and M6Tw076. Here,
![]() $R$
is the gas constant in the ideal-gas equation of state
$R$
is the gas constant in the ideal-gas equation of state
![]() $p=\unicode[STIX]{x1D70C}RT$
.
$p=\unicode[STIX]{x1D70C}RT$
.
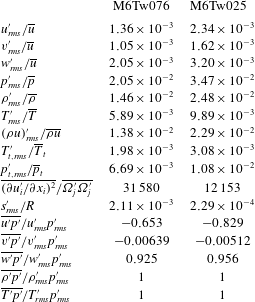
4.5 Free-stream acoustic radiation
In this section, the nature of free-stream acoustic fluctuations radiated from the turbulent boundary layer is analysed, including the modal compositions and the acoustic sources.
4.5.1 Modal compositions of free-stream fluctuations
The characteristics of free-stream fluctuations are analysed using the theory of modal analysis, which was initially proposed by Kovasznay (Reference Kovasznay1953). According to Kovasznay, the fluctuations at any point within a uniform mean flow can be represented as a superposition of three different modes with covarying physical properties: the vorticity mode, the acoustic or sound-wave mode and the entropy mode (also referred to as entropy spottiness or temperature spottiness).
Table 4 lists the free-stream values of several fluctuating flow variables for cases M6Tw025 and M6Tw076. Here,
![]() $s$
is the specific entropy,
$s$
is the specific entropy,
![]() $\unicode[STIX]{x1D6FA}$
is the vorticity and the subscript ‘
$\unicode[STIX]{x1D6FA}$
is the vorticity and the subscript ‘
![]() $t$
’ denotes stagnation quantities. A comparison of the data in the two cases indicates that the magnitude of free-stream fluctuations normalized by the respective mean values increases significantly as the wall temperature decreases, including both the velocity fluctuations and the fluctuations in thermodynamic variables. In particular, the pressure fluctuations in the free stream, including
$t$
’ denotes stagnation quantities. A comparison of the data in the two cases indicates that the magnitude of free-stream fluctuations normalized by the respective mean values increases significantly as the wall temperature decreases, including both the velocity fluctuations and the fluctuations in thermodynamic variables. In particular, the pressure fluctuations in the free stream, including
![]() $p_{rms}^{\prime }/\overline{p}$
and
$p_{rms}^{\prime }/\overline{p}$
and
![]() $p_{t,rms}^{\prime }/\overline{p}_{t}$
, are considerably different for the two cases (
$p_{t,rms}^{\prime }/\overline{p}_{t}$
, are considerably different for the two cases (
![]() $3.47\,\%$
versus
$3.47\,\%$
versus
![]() $2.05\,\%$
for
$2.05\,\%$
for
![]() $p_{rms}^{\prime }/\overline{p}$
,
$p_{rms}^{\prime }/\overline{p}$
,
![]() $1.08\,\%$
versus
$1.08\,\%$
versus
![]() $0.669\,\%$
for
$0.669\,\%$
for
![]() $p_{t,rms}^{\prime }/\overline{p}_{t}$
, larger values for the colder-wall case). However,
$p_{t,rms}^{\prime }/\overline{p}_{t}$
, larger values for the colder-wall case). However,
![]() $p_{rms}^{\prime }/\overline{p}$
and
$p_{rms}^{\prime }/\overline{p}$
and
![]() $p_{t,rms}^{\prime }/\overline{p}_{t}$
bear nearly the same ratio of approximately
$p_{t,rms}^{\prime }/\overline{p}_{t}$
bear nearly the same ratio of approximately
![]() $1.7$
across the two cases. For both wall-temperature cases, the variation in r.m.s. amplitudes of velocity fluctuations along the three Cartesian axes indicates the anisotropy of the free-stream velocity fluctuations, with the wall-normal component of the velocity fluctuations being the largest among the three. The relative perturbations in thermodynamic variables are nearly an order of magnitude larger than the velocity fluctuations and nearly satisfy isentropic relations, indicating the acoustic nature of the free-stream fluctuations. The dominance of the acoustic model is also indicated by the large ratio of the dilatational fluctuations
$1.7$
across the two cases. For both wall-temperature cases, the variation in r.m.s. amplitudes of velocity fluctuations along the three Cartesian axes indicates the anisotropy of the free-stream velocity fluctuations, with the wall-normal component of the velocity fluctuations being the largest among the three. The relative perturbations in thermodynamic variables are nearly an order of magnitude larger than the velocity fluctuations and nearly satisfy isentropic relations, indicating the acoustic nature of the free-stream fluctuations. The dominance of the acoustic model is also indicated by the large ratio of the dilatational fluctuations
![]() $\overline{(\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{i})^{2}}$
to the vortical fluctuations
$\overline{(\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{i})^{2}}$
to the vortical fluctuations
![]() $\overline{\unicode[STIX]{x1D6FA}_{j}^{\prime }\unicode[STIX]{x1D6FA}_{j}^{\prime }}$
and the small values of the entropy fluctuations
$\overline{\unicode[STIX]{x1D6FA}_{j}^{\prime }\unicode[STIX]{x1D6FA}_{j}^{\prime }}$
and the small values of the entropy fluctuations
![]() $s_{rms}^{\prime }/R$
compared with the pressure fluctuations
$s_{rms}^{\prime }/R$
compared with the pressure fluctuations
![]() $p_{rms}^{\prime }/\overline{p}$
.
$p_{rms}^{\prime }/\overline{p}$
.
Laufer (Reference Laufer1964) had assumed the
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $p^{\prime }$
fluctuations to be perfectly anticorrelated during the reduction of his hot-wire measurements based on the assumption of purely planar acoustic waves. However, the numerical simulations for both values of surface temperature ratio show that the correlation coefficient between
$p^{\prime }$
fluctuations to be perfectly anticorrelated during the reduction of his hot-wire measurements based on the assumption of purely planar acoustic waves. However, the numerical simulations for both values of surface temperature ratio show that the correlation coefficient between
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $p^{\prime }$
is different from
$p^{\prime }$
is different from
![]() $-1$
. Cooling of the surface leads to a correlation coefficient of
$-1$
. Cooling of the surface leads to a correlation coefficient of
![]() $-0.829$
for case M6Tw025, which is closer to
$-0.829$
for case M6Tw025, which is closer to
![]() $-1$
than the correlation coefficient of
$-1$
than the correlation coefficient of
![]() $-0.653$
for case M6Tw076. The less significant deviation from purely planar behaviour for case M6Tw025 may indicate that acoustic radiation becomes closer to planar acoustic waves with increased wall cooling.
$-0.653$
for case M6Tw076. The less significant deviation from purely planar behaviour for case M6Tw025 may indicate that acoustic radiation becomes closer to planar acoustic waves with increased wall cooling.

Figure 17. Profiles of the r.m.s. source terms (including the total, nonlinear source (NLS) and linear source (LS) terms) across the near-wall portion of the boundary layer. The r.m.s. values of the source terms are normalized by
![]() $(\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}^{2})^{2}$
.
$(\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}^{2})^{2}$
.
4.5.2 Acoustic sources
To understand the effect of wall cooling on the pressure field, an analysis following Phillips (Reference Phillips1960) has been carried out to study the acoustic sources that are responsible for the pressure fluctuations induced by the turbulent boundary layer. The acoustic source terms can be derived by rearranging the Navier–Stokes equations into the form of a wave equation, after neglecting the diffusive terms, as
where
![]() $S\equiv (\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j})(\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})$
is the acoustic source term, which is quadratic in the total flow velocity,
$S\equiv (\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j})(\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})$
is the acoustic source term, which is quadratic in the total flow velocity,
![]() $p_{0}$
is a convenient reference pressure,
$p_{0}$
is a convenient reference pressure,
![]() $\text{D}/\text{D}t$
is the substantial derivative based on mean flow velocity and
$\text{D}/\text{D}t$
is the substantial derivative based on mean flow velocity and
![]() $\unicode[STIX]{x1D6FE}$
is the specific heat ratio. The terms on the left-hand side of (4.8) are those of a wave equation in a medium moving with the local mean velocity of the flow. The acoustic source term
$\unicode[STIX]{x1D6FE}$
is the specific heat ratio. The terms on the left-hand side of (4.8) are those of a wave equation in a medium moving with the local mean velocity of the flow. The acoustic source term
![]() $S$
on the right-hand side can be further decomposed into its linear (rapid) component
$S$
on the right-hand side can be further decomposed into its linear (rapid) component
![]() $2(\unicode[STIX]{x2202}\bar{U}/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}x)$
and its nonlinear (slow) component
$2(\unicode[STIX]{x2202}\bar{U}/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}x)$
and its nonlinear (slow) component
![]() $(\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{j})(\unicode[STIX]{x2202}u_{j}^{\prime }/\unicode[STIX]{x2202}x_{i})$
. The details about the acoustic analogy equation, the definition and the decomposition of acoustic source terms are discussed in our previous papers (Duan et al.
Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016).
$(\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{j})(\unicode[STIX]{x2202}u_{j}^{\prime }/\unicode[STIX]{x2202}x_{i})$
. The details about the acoustic analogy equation, the definition and the decomposition of acoustic source terms are discussed in our previous papers (Duan et al.
Reference Duan, Choudhari and Wu2014, Reference Duan, Choudhari and Zhang2016).
Figure 17 plots the r.m.s. of the acoustic source term,
![]() $S_{rms}^{\prime }$
, and its linear and nonlinear components in the near-wall region of the boundary layer against wall-normal distance. For both wall temperatures, the near-wall variation of the total acoustic source term conforms well with that of
$S_{rms}^{\prime }$
, and its linear and nonlinear components in the near-wall region of the boundary layer against wall-normal distance. For both wall temperatures, the near-wall variation of the total acoustic source term conforms well with that of
![]() $p_{rms}^{\prime }$
(figure 5
b). For case M6Tw076, the nonlinear source term is dominant over the linear term throughout the boundary layer (figure 17
a), and
$p_{rms}^{\prime }$
(figure 5
b). For case M6Tw076, the nonlinear source term is dominant over the linear term throughout the boundary layer (figure 17
a), and
![]() $(\unicode[STIX]{x2202}v^{\prime }/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}y)$
has the largest r.m.s. value among the constituent terms of the nonlinear acoustic source (figure 17
c). The dominance of
$(\unicode[STIX]{x2202}v^{\prime }/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}y)$
has the largest r.m.s. value among the constituent terms of the nonlinear acoustic source (figure 17
c). The dominance of
![]() $(\unicode[STIX]{x2202}v^{\prime }/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}y)$
may be indicative of the important role played by streamwise vortical structures in sound generation (Duan et al.
Reference Duan, Choudhari and Zhang2016).
$(\unicode[STIX]{x2202}v^{\prime }/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}y)$
may be indicative of the important role played by streamwise vortical structures in sound generation (Duan et al.
Reference Duan, Choudhari and Zhang2016).
As the wall temperature is decreased, the r.m.s. of the nonlinear acoustic term is significantly reduced in the buffer layer due to the damping of
![]() $(\unicode[STIX]{x2202}v^{\prime }/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}y)$
, and the linear source term becomes relatively more dominant in this region (figure 17
b). In the meantime, the r.m.s. value of the nonlinear acoustic term is dramatically increased in the viscous sublayer, with
$(\unicode[STIX]{x2202}v^{\prime }/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}y)$
, and the linear source term becomes relatively more dominant in this region (figure 17
b). In the meantime, the r.m.s. value of the nonlinear acoustic term is dramatically increased in the viscous sublayer, with
![]() $(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}z)^{2}$
becoming the most dominant term in this region (figure 17
c). Given that
$(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}z)^{2}$
becoming the most dominant term in this region (figure 17
c). Given that
![]() $(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}z)^{2}$
is related to the dilatational fluctuations of velocity and
$(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}z)^{2}$
is related to the dilatational fluctuations of velocity and
![]() $(\unicode[STIX]{x2202}v^{\prime }/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}y)$
is related to the near-wall streamwise vortical fluctuations, the variation of these terms with wall temperature may indicate that wall cooling influences sound generation largely by enhancing dilatational motions in the viscous sublayer while damping streamwise vortical structures in the buffer layer. The enhancement of the dilatational motions in the viscous sublayer and the damping of the streamwise vortical structures in the boundary layer are also apparent from the rapid increase in r.m.s. dilation and r.m.s. streamwise vorticity near the wall, as seen from figures 18(a) and 18(b). The enhancement of dilatational motions near the wall is not unexpected as wall cooling increases the turbulent Mach number by causing a decrease in the local sound speed.
$(\unicode[STIX]{x2202}v^{\prime }/\unicode[STIX]{x2202}z)(\unicode[STIX]{x2202}w^{\prime }/\unicode[STIX]{x2202}y)$
is related to the near-wall streamwise vortical fluctuations, the variation of these terms with wall temperature may indicate that wall cooling influences sound generation largely by enhancing dilatational motions in the viscous sublayer while damping streamwise vortical structures in the buffer layer. The enhancement of the dilatational motions in the viscous sublayer and the damping of the streamwise vortical structures in the boundary layer are also apparent from the rapid increase in r.m.s. dilation and r.m.s. streamwise vorticity near the wall, as seen from figures 18(a) and 18(b). The enhancement of dilatational motions near the wall is not unexpected as wall cooling increases the turbulent Mach number by causing a decrease in the local sound speed.

Figure 18. Profiles of the r.m.s. of dilatation and streamwise vorticity across the near-wall portion of the boundary layer normalized using
![]() $\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}^{2}$
.
$\unicode[STIX]{x1D708}_{w}/u_{\unicode[STIX]{x1D70F}}^{2}$
.
Figure 19 compares the phase speed derived from the acoustic source term,
![]() $U_{s}(\unicode[STIX]{x1D714})$
, between cases M6Tw025 and M6Tw076 in the buffer layer. Wall cooling increases the convection speed of the acoustic sources for all frequencies. At the dominant frequency of free-stream acoustic radiation,
$U_{s}(\unicode[STIX]{x1D714})$
, between cases M6Tw025 and M6Tw076 in the buffer layer. Wall cooling increases the convection speed of the acoustic sources for all frequencies. At the dominant frequency of free-stream acoustic radiation,
![]() $\unicode[STIX]{x1D714}_{pk}\unicode[STIX]{x1D6FF}/U_{\infty }=1.5$
, which corresponds to the peak frequency of the premultiplied spectrum shown in figure 7(c), the convection speed of the acoustic source is
$\unicode[STIX]{x1D714}_{pk}\unicode[STIX]{x1D6FF}/U_{\infty }=1.5$
, which corresponds to the peak frequency of the premultiplied spectrum shown in figure 7(c), the convection speed of the acoustic source is
![]() $0.64U_{\infty }$
(
$0.64U_{\infty }$
(
![]() $M_{r}=2.11$
) and
$M_{r}=2.11$
) and
![]() $0.55U_{\infty }$
(
$0.55U_{\infty }$
(
![]() $M_{r}=2.64$
) respectively for cases M6Tw025 and M6Tw076, with
$M_{r}=2.64$
) respectively for cases M6Tw025 and M6Tw076, with
![]() $M_{r}\equiv (U_{\infty }-U_{s})/a_{\infty }$
. The fact that acoustic sources propagate supersonically with respect to the free stream is consistent with the concept of ‘eddy Mach wave’ radiation (Phillips Reference Phillips1960). Given that the radiation wave angle can be approximated via the ‘Mach angle’ relation as
$M_{r}\equiv (U_{\infty }-U_{s})/a_{\infty }$
. The fact that acoustic sources propagate supersonically with respect to the free stream is consistent with the concept of ‘eddy Mach wave’ radiation (Phillips Reference Phillips1960). Given that the radiation wave angle can be approximated via the ‘Mach angle’ relation as
![]() $1/\sin \unicode[STIX]{x1D703}=M_{r}$
, the smaller value of
$1/\sin \unicode[STIX]{x1D703}=M_{r}$
, the smaller value of
![]() $M_{r}$
for case M6Tw025 is consistent with the larger radiation wave angle of
$M_{r}$
for case M6Tw025 is consistent with the larger radiation wave angle of
![]() $28^{\circ }$
for this case (figure 10
b).
$28^{\circ }$
for this case (figure 10
b).

Figure 19. The phase speed of the acoustic source term. Here,
![]() $U_{s}(\unicode[STIX]{x1D714})$
is defined based on (4.7) for the acoustic source term
$U_{s}(\unicode[STIX]{x1D714})$
is defined based on (4.7) for the acoustic source term
![]() $S$
.
$S$
.
5 Summary and conclusions
Direct numerical simulations of Mach 5.86 turbulent boundary layers with two wall temperatures (
![]() $T_{w}/T_{r}=0.25$
,
$T_{w}/T_{r}=0.25$
,
![]() $0.76$
) are compared to investigate the effect of wall cooling on the pressure fluctuations generated by hypersonic turbulent boundary layers. The simulations show that wall cooling significantly modifies the pressure-fluctuation intensities near the wall, with
$0.76$
) are compared to investigate the effect of wall cooling on the pressure fluctuations generated by hypersonic turbulent boundary layers. The simulations show that wall cooling significantly modifies the pressure-fluctuation intensities near the wall, with
![]() $p_{w,rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
varying from
$p_{w,rms}^{\prime }/\unicode[STIX]{x1D70F}_{w}$
varying from
![]() $2.8$
for
$2.8$
for
![]() $T_{w}/T_{r}=0.76$
to
$T_{w}/T_{r}=0.76$
to
![]() $3.5$
for
$3.5$
for
![]() $T_{w}/T_{r}=0.25$
. Furthermore, the frequency spectra of the wall-pressure fluctuations for the two cases show considerable differences when plotted in terms of either outer-layer or inner-layer variables. The peak of the premultiplied spectrum shifts to a higher value as the wall temperature decreases. Wall cooling slows down the evolution of pressure wavepackets at the wall, resulting in a larger decorrelation length of pressure structures, but has little influence on the bulk propagation speeds of wall-pressure structures. Regarding the free-stream pressure fluctuations, although the intensity shows a strong wall-temperature dependence when normalized by the mean free-stream pressure (
$T_{w}/T_{r}=0.25$
. Furthermore, the frequency spectra of the wall-pressure fluctuations for the two cases show considerable differences when plotted in terms of either outer-layer or inner-layer variables. The peak of the premultiplied spectrum shifts to a higher value as the wall temperature decreases. Wall cooling slows down the evolution of pressure wavepackets at the wall, resulting in a larger decorrelation length of pressure structures, but has little influence on the bulk propagation speeds of wall-pressure structures. Regarding the free-stream pressure fluctuations, although the intensity shows a strong wall-temperature dependence when normalized by the mean free-stream pressure (
![]() $\overline{p}_{\infty }$
), it compares well between the two cases when normalized by the local wall shear stress
$\overline{p}_{\infty }$
), it compares well between the two cases when normalized by the local wall shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
. The frequency spectra of free-stream radiation collapse well between the two cases when normalized in terms of outer or inner boundary-layer parameters. Wall cooling results in an increase in the radiation wave angle (defined based on spatial correlations,
$\unicode[STIX]{x1D70F}_{w}$
. The frequency spectra of free-stream radiation collapse well between the two cases when normalized in terms of outer or inner boundary-layer parameters. Wall cooling results in an increase in the radiation wave angle (defined based on spatial correlations,
![]() $C_{pp}$
) from
$C_{pp}$
) from
![]() $21^{\circ }$
for
$21^{\circ }$
for
![]() $T_{w}/T_{r}=0.76$
to
$T_{w}/T_{r}=0.76$
to
![]() $28^{\circ }$
for
$28^{\circ }$
for
![]() $T_{w}/T_{r}=0.25$
. Similarly to pressure structures at the wall, the free-stream pressure structures evolve less rapidly as the wall temperature decreases. The propagation speed of free-stream pressure structures is found to be insensitive to the wall temperature and is significantly smaller than the free-stream velocity for both cases. An analysis of acoustic sources using the acoustic analogy of Phillips (Reference Phillips1960) shows that wall cooling influences sound generation largely by enhancing dilatational motions in the viscous sublayer while damping streamwise vortical structures in the buffer layer.
$T_{w}/T_{r}=0.25$
. Similarly to pressure structures at the wall, the free-stream pressure structures evolve less rapidly as the wall temperature decreases. The propagation speed of free-stream pressure structures is found to be insensitive to the wall temperature and is significantly smaller than the free-stream velocity for both cases. An analysis of acoustic sources using the acoustic analogy of Phillips (Reference Phillips1960) shows that wall cooling influences sound generation largely by enhancing dilatational motions in the viscous sublayer while damping streamwise vortical structures in the buffer layer.
Acknowledgements
This material is based on work supported by the Air Force Office of Scientific Research through award no. FA9550-14-1-0170, managed by Dr I. Leyva. The work was initiated with support of the NASA Langley Research Center under the Research Cooperative agreement no. NNL09AA00A (through the National Institute of Aerospace). Computational resources were provided by the NASA Advanced Supercomputing Division, the DoD High Performance Computing Modernization Program and the NSF’s PRAC program (NSF ACI-1640865).