Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hinton, Edward M.
and
Woods, Andrew W.
2020.
Shear dispersion in a porous medium. Part 1. An intrusion with a steady shape.
Journal of Fluid Mechanics,
Vol. 899,
Issue. ,
Hinton, Edward M.
and
Woods, Andrew W.
2020.
Shear dispersion in a porous medium. Part 2. An intrusion with a growing shape.
Journal of Fluid Mechanics,
Vol. 899,
Issue. ,
Hinton, Edward M.
2020.
Axisymmetric viscous flow between two horizontal plates.
Physics of Fluids,
Vol. 32,
Issue. 6,
Hinton, Edward M.
and
Woods, Andrew W.
2021.
Capillary trapping in a vertically heterogeneous porous layer.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
Ma, Ziqi
Dong, Shuning
Yin, Shangxian
Dai, Zhenxue
Zhu, Lin
Jia, Wei
Wallace, Corey
and
Soltanian, Mohamad Reza
2021.
Experimental investigations on scale-dependent dispersivity in three-dimensional heterogeneous porous media.
Environmental Science and Pollution Research,
Vol. 28,
Issue. 18,
p.
23336.
Hinton, E. M.
and
Hogg, A. J.
2021.
Modeling the Influence of a Variable Permeability Inclusion on Free‐Surface Flow in an Inclined Aquifer.
Water Resources Research,
Vol. 57,
Issue. 4,
Ren, Bo
Jensen, Jerry
Lake, Larry
Duncan, Ian
and
Male, Frank
2021.
Analysis of Vertical Permeability and Its Influence on CO2 EOR and Storage in a Carbonate Reservoir.
Penney, Jared
and
Stastna, Marek
2021.
Numerical simulations of flow through a variable permeability circular cylinder.
Physics of Fluids,
Vol. 33,
Issue. 11,
Ren, Bo
Jensen, Jerry L.
Lake, Larry W.
Duncan, Ian J.
and
Male, Frank
2022.
Analysis of Vertical Permeability and Its Influence on CO2 Enhanced Oil Recovery and Storage in a Carbonate Reservoir.
SPE Reservoir Evaluation & Engineering,
Vol. 25,
Issue. 03,
p.
414.
Zheng, Zhong
2022.
Upscaling unsaturated flows in vertically heterogeneous porous layers.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Ren, Bo
Jensen, Jerry
Duncan, Ian
and
Lake, Larry
2022.
Buoyant Flow of H2 Versus CO2 in Storage Aquifers.
Zheng, Zhong
and
Stone, Howard A.
2022.
The Influence of Boundaries on Gravity Currents and Thin Films: Drainage, Confinement, Convergence, and Deformation Effects.
Annual Review of Fluid Mechanics,
Vol. 54,
Issue. 1,
p.
27.
Zeighami, Farhad
Lenci, Alessandro
and
Di Federico, Vittorio
2022.
Drainage of power-law fluids from fractured or porous finite domains.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 305,
Issue. ,
p.
104832.
Sahu, Chunendra K.
and
Neufeld, Jerome A.
2023.
Experimental insights into gravity-driven flows and mixing in layered porous media.
Journal of Fluid Mechanics,
Vol. 956,
Issue. ,
Zheng, Zhong
2023.
The radial slump of a gravity current in a confined porous layer.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 479,
Issue. 2270,
Ren, Bo
Jensen, Jerry
Duncan, Ian
and
Lake, Larry
2023.
Buoyant Flow of H2 Vs. CO2 in Storage Aquifers: Implications to Geological Screening.
SPE Reservoir Evaluation & Engineering,
Vol. 26,
Issue. 03,
p.
1048.
Jia, Cunqi
Ren, Bo
Sepehrnoori, Kamy
Delshad, Mojdeh
Liu, Boyu
Sun, Hai
and
Yao, Jun
2023.
Numerical studies of hydrogen buoyant flow in storage aquifers.
Fuel,
Vol. 349,
Issue. ,
p.
128755.
Sheikhi, S.
Sahu, C.K.
and
Flynn, M.R.
2023.
Dispersion effects in porous medium gravity currents experiencing local drainage.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Zheng, Zhong
2023.
The capillary pressure curves from upscaling interfacial and unsaturated flows in porous layers with vertical heterogeneity.
Theoretical and Applied Mechanics Letters,
Vol. 13,
Issue. 4,
p.
100467.
Yang, Kaien
and
Zheng, Zhong
2024.
Dynamic interaction of gravity currents in a confined porous layer.
Journal of Fluid Mechanics,
Vol. 979,
Issue. ,
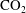 $\text{CO}_{2}$ or gas injected into subsurface reservoirs.
$\text{CO}_{2}$ or gas injected into subsurface reservoirs.

