Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T18:37:29.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of velocity ratio on the interaction between plasma synthetic jets and turbulent cross-flow

Published online by Cambridge University Press:  28 February 2019

Haohua Zong Open the ORCID record for Haohua Zong [Opens in a new window]  and
Marios Kotsonis
Haohua Zong*
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HS Delft, The Netherlands
Marios Kotsonis
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HS Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Plasma synthetic jet actuators (PSJAs) are particularly suited for high-Reynolds-number, high-speed flow control due to their unique capability of generating supersonic pulsed jets at high frequency (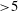${>}5$  kHz). Different from conventional synthetic jets driven by oscillating piezoelectric diaphragms, the exit-velocity variation of plasma synthetic jets (PSJs) within one period is significantly asymmetric, with ingestion being relatively weaker (less than 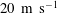$20~\text{m}~\text{s}^{-1}$) and longer than ejection. In this study, high-speed phase-locked particle image velocimetry is employed to investigate the interaction between PSJAs (round exit orifice, diameter 2 mm) and a turbulent boundary layer at constant Strouhal number (0.02) and increasing mean velocity ratio ($r$, defined as the ratio of the time-mean velocity over the ejection phase to the free-stream velocity). Two distinct operational regimes are identified for all the tested cases, separated by a transition velocity ratio, lying between 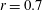$r=0.7$ and 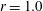$r=1.0$. At large velocity and stroke ratios (first regime, representative case 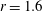$r=1.6$), vortex rings are followed by a trailing jet column and tilt downstream initially. This downstream tilting is transformed into upstream tilting after the pinch-off of the trailing jet column. The moment of this transformation relative to the discharge advances with decreasing velocity ratio. Shear-layer vortices (SVs) and a hanging vortex pair (HVP) are identified in the windward and leeward sides of the jet body, respectively. The HVP is initially erect and evolves into an inclined primary counter-rotating vortex pair (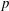$p$-CVP) which branches from the middle of the front vortex ring and extends to the near-wall region. The two legs of the 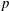$p$-CVP are bridged by SVs, and a secondary counter-rotating vortex pair ($s$-CVP) is induced underneath these two legs. At low velocity and stroke ratios (second regime, representative case 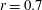$r=0.7$), the trailing jet column and 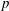$p$-CVP are absent. Vortex rings always tilt upstream, and the pitching angle increases monotonically with time. An $s$-CVP in the near-wall region is induced directly by the two longitudinal edges of the ring. Inspection of spanwise planes (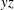$yz$-plane) reveals that boundary-layer energization is realized by the downwash effect of either vortex rings or 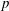$p$-CVP. In addition, in the streamwise symmetry plane, the increasing wall shear stress is attributed to the removal of low-energy flow by ingestion. The downwash effect of the $s$-CVP does not benefit boundary-layer energization, as the flow swept to the wall is of low energy.

JFM classification

Boundary Layers: Boundary layer control Wakes/Jets: Jets Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 928 - 962
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amitay, M., Smith, D. R., Kibens, V., Parekh, D. E. & Glezer, A. 2001 Aerodynamic flow control over an unconventional airfoil using synthetic jet actuators. AIAA J. 39 (3), 361–370.10.2514/2.1323Google Scholar
Anderson, K. V. & Knight, D. D. 2012 Plasma jet for flight control. AIAA J. 50 (9), 1855–1872.10.2514/1.J051309Google Scholar
Belinger, A., Hardy, P., Barricau, P., Cambronne, J. P. & Caruana, D. 2011 Influence of the energy dissipation rate in the discharge of a plasma synthetic jet actuator. J. Phys. D 44 (36), 365201.Google Scholar
Belinger, A., Naudé, N., Cambronne, J. P. & Caruana, D. 2014 Plasma synthetic jet actuator: electrical and optical analysis of the discharge. J. Phys. D 47 (34), 345202.Google Scholar
Bons, J. P., Sondergaard, R. & Rivir, R. B. 2000 Turbine separation control using pulsed vortex generator jets. In ASME Turbo Expo 2000: Power for Land, Sea, and Air. pp. V003T01A067–V003T01A067. American Society of Mechanical Engineers.Google Scholar
Breidenthal, R. E. 1984 Structure and mixing of a transverse jet in incompressible flow. J. Fluid Mech. 148, 405–412.Google Scholar
Cattafesta, L. N. & Sheplak, M. 2011 Actuators for active flow control. Annu. Rev. Fluid Mech. 43 (1), 247–272.10.1146/annurev-fluid-122109-160634Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.10.1017/S0022112005004726Google Scholar
Chedevergne, F., Léon, O., Bodoc, V. & Caruana, D. 2015 Experimental and numerical response of a high-Reynolds-number jet to a plasma synthetic jet actuator. Intl J. Heat Fluid Flow 56, 1–15.10.1016/j.ijheatfluidflow.2015.06.008Google Scholar
Chiatto, M., Capuano, F., Coppola, G. & de Luca, L. 2017 LEM characterization of synthetic jet actuators driven by piezoelectric element: a review. Sensors 17 (6), 1216.10.3390/s17061216Google Scholar
Chiatto, M. & de Luca, L. 2017 Numerical and experimental frequency response of plasma synthetic jet actuators. In 55th AIAA Aerospace Sciences Meeting, 1884. American Institute of Aeronautics and Astronautics.Google Scholar
Christensen, K. T. 2004 The influence of peak-locking errors on turbulence statistics computed from PIV ensembles. Exp. Fluids 36 (3), 484–497.10.1007/s00348-003-0754-2Google Scholar
Compton, D. & Johnston, J. 1992 Streamwise vortex production by pitched and skewed jets in a turbulent boundary layer. AIAA J. 30 (3), 640–647.10.2514/3.10967Google Scholar
Crittenden, T. M. & Glezer, A. 2006 A high-speed, compressible synthetic jet. Phys. Fluids 18 (1), 017107.10.1063/1.2166451Google Scholar
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 574, 25–58.Google Scholar
Emerick, T., Ali, M. Y., Foster, C., Alvi, F. S. & Popkin, S. 2014 SparkJet characterizations in quiescent and supersonic flowfields. Exp. Fluids 55 (12), 1–21.10.1007/s00348-014-1858-6Google Scholar
Gallas, Q., Carroll, B., Cattafesta, L., Holman, R., Nishida, T. & Sheplak, M. 2003 Lumped element modeling of piezoelectric-driven synthetic jet Actuators. AIAA J. 41 (2), 240–247.10.2514/2.1936Google Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.10.1017/S0022112097008410Google Scholar
Glezer, A. & Amitay, M. 2002 Synthetic jets. Annu. Rev. Fluid Mech. 34, 503–529.10.1146/annurev.fluid.34.090501.094913Google Scholar
Glezer, A., Amitay, M. & Honohan, A. M. 2005 Aspects of low- and high-frequency actuation for aerodynamic flow control. AIAA J. 43 (7), 1501–1511.10.2514/1.7411Google Scholar
Greene, B. R., Clemens, N. T., Magari, P. & Micka, D. 2015 Control of mean separation in shock boundary layer interaction using pulsed plasma jets. Shock Waves 25 (5), 495–505.10.1007/s00193-014-0524-5Google Scholar
Grossman, K., Bohdan, C. & Vanwie, D. 2003 Sparkjet actuators for flow control. In 41st Aerospace Sciences Meeting and Exhibit, 57. American Institute of Aeronautics and Astronautics.Google Scholar
Holman, R., Utturkar, Y., Mittal, R., Smith, B. L. & Cattafesta, L. 2005 Formation criterion for synthetic jets. AIAA J. 43 (10), 2110–2116.10.2514/1.12033Google Scholar
Jabbal, M. & Zhong, S. 2007 Flow measurement of synthetic jets in a boundary layer. In 37th AIAA Fluid Dynamics Conference and Exhibit, 3852. American Institute of Aeronautics and Astronautics.Google Scholar
Jabbal, M. & Zhong, S. 2008 The near wall effect of synthetic jets in a boundary layer. Intl J. Heat Fluid Flow 29 (1), 119–130.10.1016/j.ijheatfluidflow.2007.07.011Google Scholar
Jabbal, M. & Zhong, S. 2010 Particle image velocimetry measurements of the interaction of synthetic jets with a zero-pressure gradient laminar boundary layer. Phys. Fluids 22 (6), 1–17.10.1063/1.3432133Google Scholar
Johnston, J. P. & Nishi, M. 1990 Vortex generator jets – means for flow separation control. AIAA J. 28 (6), 989–994.10.2514/3.25155Google Scholar
Kelso, R. M., Lim, T. T. & Perry, a. E. 1996 An experimental study of round jets in cross-flow. J. Fluid Mech. 306, 111–144.10.1017/S0022112096001255Google Scholar
Lardeau, S. & Leschziner, M. A. 2011 The interaction of round synthetic jets with a turbulent boundary layer separating from a rounded ramp. J. Fluid Mech. 683, 172–211.10.1017/jfm.2011.258Google Scholar
Laurendeau, F., Léon, O., Chedevergne, F., Senoner, J.-M. & Casalis, G. 2017 Particle image velocimetry experiment analysis using large-eddy simulation: application to plasma actuators. AIAA J. 55 (11), 3767–3780.10.2514/1.J055687Google Scholar
Lin, J. C. 2002 Review of research on low-profile vortex generators to control boundary-layer separation. Prog. Aerosp. Sci. 38 (4–5), 389–420.10.1016/S0376-0421(02)00010-6Google Scholar
de Luca, L., Girfoglio, M. & Coppola, G. 2014 Modeling and experimental validation of the frequency response of synthetic jet actuators. AIAA J. 52 (8), 1733–1748.10.2514/1.J052674Google Scholar
Mahesh, K. 2013 The interaction of jets with crossflow. Annu. Rev. Fluid Mech. 45 (1), 379–407.10.1146/annurev-fluid-120710-101115Google Scholar
Margason, R. J 1993 Fifty years of jet in cross flow research. In AGARD CP 534, paper 1. AGARD.Google Scholar
M’Closkey, R. T., King, J. M., Cortelezzi, L. & Karagozian, A. R. 2002 The actively controlled jet in crossflow. J. Fluid Mech. 452, 325–335.10.1017/S0022112001006589Google Scholar
Meyer, K. E., Pedersen, J. M. & Özcan, O. 2007 A turbulent jet in crossflow analysed with proper orthogonal decomposition. J. Fluid Mech. 583, 199–227.10.1017/S0022112007006143Google Scholar
Mittal, R. & Rampunggoon, P. 2002 On the virtual aeroshaping effect of synthetic jets. Phys. Fluids 14 (4), 1533–1536.10.1063/1.1453470Google Scholar
Muppidi, S. & Mahesh, K. 2005 Study of trajectories of jets in crossflow using direct numerical simulations. J. Fluid Mech. 530, 81–100.10.1017/S0022112005003514Google Scholar
Narayanaswamy, V., Raja, L. L. & Clemens, N. T. 2010 Characterization of a high-frequency pulsed-plasma jet actuator for supersonic flow control. AIAA J. 48 (2), 297–305.10.2514/1.41352Google Scholar
Narayanaswamy, V., Raja, L. L. & Clemens, N. T. 2012 Control of unsteadiness of a shock wave/turbulent boundary layer interaction by using a pulsed-plasma-jet actuator. Phys. Fluids 24 (7), 076101.10.1063/1.4731292Google Scholar
Reedy, T. M., Kale, N. V., Dutton, J. C. & Elliott, G. S. 2013 Experimental characterization of a pulsed plasma jet. AIAA J. 51 (8), 2027–2031.10.2514/1.J052022Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.10.1017/S0022112072000679Google Scholar
Sau, R. & Mahesh, K. 2007 Passive scalar mixing in vortex rings. J. Fluid Mech. 582, 449–461.10.1017/S0022112007006349Google Scholar
Sau, R. & Mahesh, K. 2008 Dynamics and mixing of vortex rings in crossflow. J. Fluid Mech. 604, 389–409.10.1017/S0022112008001328Google Scholar
Sau, R. & Mahesh, K. 2010 Optimization of pulsed jets in crossflow. J. Fluid Mech. 653, 365–390.10.1017/S0022112010000388Google Scholar
Schlichting, H. & Gersten, K. 2017 Boundary-layer Theory. Springer.10.1007/978-3-662-52919-5Google Scholar
Sciacchitano, A. & Wieneke, B. 2016 PIV uncertainty propagation. Meas. Sci. Technol. 27 (8), 084006.10.1088/0957-0233/27/8/084006Google Scholar
Seifert, A., Bachar, T., Koss, D., Shepshelovich, M. & Wygnanskil, I. 1993 Oscillatory blowing: a tool to delay boundary-layer separation. AIAA J. 31 (11), 2052–2060.Google Scholar
Smith, B. L. & Glezer, A. 1998 The formation and evolution of synthetic jets. Phys. Fluids 10 (9), 2281–2297.10.1063/1.869828Google Scholar
Smith, B. L. & Glezer, A. 2002 Jet vectoring using synthetic jets. J. Fluid Mech. 458, 1–34.10.1017/S0022112001007406Google Scholar
Smith, B. L. & Swift, G. W. 2003 A comparison between synthetic jets and continuous jets. Exp. Fluids 34 (4), 467–472.10.1007/s00348-002-0577-6Google Scholar
Smith, S. H. & Mungal, M. G. 1998 Mixing, structure and scaling of the jet in crossflow. J. Fluid Mech. 357, 83–122.10.1017/S0022112097007891Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164 (919), 476–490.10.1098/rspa.1938.0032Google Scholar
Wu, J., Ma, H. & Zhou, M. 2007 Vorticity and Vortex Dynamics. Springer.Google Scholar
Wu, X., Moin, P., Wallace, J. M., Skarda, J., Lozano-Durán, A. & Hickey, J. P. 2017 Transitional–turbulent spots and turbulent–turbulent spots in boundary layers. Proc. Natl Acad Sci. USA 114 (27), E5292–E5299.10.1073/pnas.1704671114Google Scholar
Yuan, L. L. & Street, R. L. 1998 Trajectory and entrainment of a round jet in crossflow. Phys. Fluids 10 (9), 2323–2335.10.1063/1.869751Google Scholar
Yuan, L. L., Street, R. L. & Ferziger, J. H. 1999 Large-eddy simulations of a round jet in crossflow. J. Fluid Mech. 379, 71–104.10.1017/S0022112098003346Google Scholar
Zhang, S. & Zhong, S. 2011 Turbulent flow separation control over a two-dimensional ramp using synthetic jets. AIAA J. 49 (12), 2637–2649.10.2514/1.J051046Google Scholar
Zhou, J. & Zhong, S. 2009 Numerical simulation of the interaction of a circular synthetic jet with a boundary layer. Comput. Fluids 38 (2), 393–405.10.1016/j.compfluid.2008.04.012Google Scholar
Zong, H., Cui, W., Wu, Y., Zhang, Z., Liang, H., Jia, M. & Li, Y. 2015a Influence of capacitor energy on performance of a three-electrode plasma synthetic jet actuator. Sensors Actuators A 222, 114–121.10.1016/j.sna.2014.11.022Google Scholar
Zong, H. & Kotsonis, M. 2016a Characterisation of plasma synthetic jet actuators in quiescent flow. J. Phys. D 49 (33), 335202.Google Scholar
Zong, H. & Kotsonis, M. 2016b Electro-mechanical efficiency of plasma synthetic jet actuator driven by capacitive discharge. J. Phys. D 49 (45), 455201.Google Scholar
Zong, H. & Kotsonis, M. 2017a Effect of slotted exit orifice on performance of plasma synthetic jet actuator. Exp. Fluids 58, 1–17.10.1007/s00348-016-2299-1Google Scholar
Zong, H. & Kotsonis, M. 2017b Experimental investigation on frequency characteristics of plasma synthetic jets. Phys. Fluids 29 (11), 115107.10.1063/1.5004634Google Scholar
Zong, H. & Kotsonis, M. 2017c Interaction between plasma synthetic jet and subsonic turbulent boundary layer. Phys. Fluids 29 (4), 045104.10.1063/1.4979527Google Scholar
Zong, H. & Kotsonis, M. 2018 Formation, evolution and scaling of plasma synthetic jets. J. Fluid Mech. 837, 147–181.10.1017/jfm.2017.855Google Scholar
Zong, H., Wu, Y., Li, Y., Song, H., Zhang, Z. & Jia, M. 2015b Analytic model and frequency characteristics of plasma synthetic jet actuator. Phys. Fluids 27 (2), 027105.10.1063/1.4908071Google Scholar