Published online by Cambridge University Press: 28 November 2023
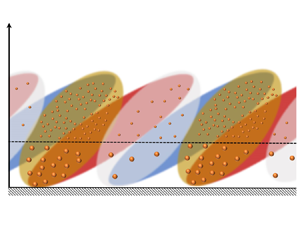
The spatial relationship between turbulent and particle concentration structures is investigated based on the turbulent velocity and particle concentration data obtained synchronously at the Qingtu Lake Observation Array site. In addition to the observation of particle concentration structures that contain not only large-scale coherence but also significant energy in the high-Reynolds-number atmospheric surface layer (ASL), the scale of turbulent motions that have the most significant coherence with particle concentration is found to follow a 1/2 power scaling law with the local height and ASL thickness. Moreover, large-scale turbulent velocity fluctuations have a significant amplitude modulation effect on particle concentration fluctuations, but the modulating influence is different for small dust particles and large saltating particles. Based on the interphase amplitude modulation, there exists a particle–turbulence structure phase difference that varies with height, which further makes the structure inclination angle of the particle concentration larger than that of the turbulence. In this scenario, a conceptual model reflecting the relationship between the two is proposed, and a quantitative formulation is further derived and found to be in good agreement with the experimental results. These findings and the proposed model contribute insights into particle–turbulence interactions, thereby providing theoretical support for a unified model of turbulence dynamics and particle kinematics.