Published online by Cambridge University Press: 25 October 2013
The effect of insoluble surfactant on the interfacial waves in connection with a two-layer channel flow is investigated for low to moderate values of the Reynolds number. Previous studies focusing on Stokes flow (Frenkel & Halpern, Phys. Fluids, vol. 14, 2002, p. L45; Halpern & Frenkel, J. Fluid Mech., vol. 485, 2003, pp. 191–220) are extended by including the inertial effect and the study of low-Reynolds-number flow (Blyth & Pozrikidis, J. Fluid Mech., vol. 521, 2004b, pp. 241–250) is enlarged up to moderate Reynolds number. Linear stability analysis based on the Orr–Sommerfeld boundary value problem identifies a surfactant mode together with an interface mode. The presence of surfactant on the interfacial mode is stabilizing at high viscosity ratio and destabilizing at low viscosity ratio. The threshold of instability is determined as a function of the Marangoni number. A long-wave model is developed to predict the families of nonlinear waves in the neighbourhood of the threshold of instability. Far from the threshold, wave dynamics is explored under the framework of a three-equation model in terms of lower layer flow rate 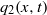 ${q}_{2} (x, t)$, lower liquid-layer thickness
${q}_{2} (x, t)$, lower liquid-layer thickness 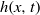 $h(x, t)$ and surfactant concentration
$h(x, t)$ and surfactant concentration 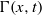 $\Gamma (x, t)$. Primary instability analysis of a three-equation model captures the result of the Orr–Sommerfeld boundary value problem very well for quite large values of wavenumber. In the nonlinear regime, travelling wave solutions demonstrate deceleration of maximum amplitude and acceleration of speed with the Marangoni number at high viscosity ratio
$\Gamma (x, t)$. Primary instability analysis of a three-equation model captures the result of the Orr–Sommerfeld boundary value problem very well for quite large values of wavenumber. In the nonlinear regime, travelling wave solutions demonstrate deceleration of maximum amplitude and acceleration of speed with the Marangoni number at high viscosity ratio 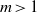 $m\gt 1$ and show completely the opposite behaviour at low viscosity ratio
$m\gt 1$ and show completely the opposite behaviour at low viscosity ratio 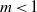 $m\lt 1$. However, both maximum amplitude and speed attain a fixed value with increasing Reynolds number and this leads to saturation of instability.
$m\lt 1$. However, both maximum amplitude and speed attain a fixed value with increasing Reynolds number and this leads to saturation of instability.