Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-08T05:32:27.442Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of small roughness elements on thermal statistics of a turbulent boundary layer at moderate Reynolds number

Published online by Cambridge University Press:  08 December 2015

Ali Doosttalab ,
Guillermo Araya ,
Jensen Newman ,
Ronald J. Adrian ,
Kenneth Jansen  and
Luciano Castillo
Ali Doosttalab
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
Guillermo Araya*
Affiliation:
Department of Mechanical Engineering, University of Puerto Rico – Mayagüez, PR 00681, USA
Jensen Newman
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
Ronald J. Adrian
Affiliation:
School for Engineering of Matter, Transport and Energy, Arizona State University, P.O. Box 876106, Tempe, AZ 85287-6106, USA
Kenneth Jansen
Affiliation:
Department of Aerospace Engineering Sciences, University of Colorado at Boulder, Boulder, CO 80309, USA
Luciano Castillo
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A zero-pressure-gradient turbulent boundary layer flowing over a transitionally rough surface (24-grit sandpaper) with 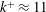$k^{+}\approx 11$ and a momentum-thickness Reynolds number of approximately 2400 is studied using direct numerical simulation (DNS). Heat transfer between the isothermal rough surface and the turbulent flow with molecular Prandtl number $Pr=0.71$ is simulated. The dynamic multiscale approach developed by Araya et al. (J. Fluid Mech., vol. 670, 2011, pp. 581–605) is employed to prescribe realistic time-dependent thermal inflow boundary conditions. In general, the rough surface reduces mean and fluctuating temperature profiles with respect to the smooth surface flow when normalized by Wang & Castillo (J. Turbul., vol. 4, 2003, 006) inner/outer scaling. It is shown that the Reynolds analogy does not hold for 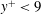$y^{+}<9$. In this region the value of the turbulent Prandtl number departs substantially from unity. Above this region the Reynolds analogy is only approximately valid, with the turbulent Prandtl number decreasing from 1 to 0.7 across the boundary layer for rough and smooth walls. In comparison with the smooth-wall case, the turbulent transport of heat per unit mass, 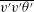$\overline{v^{\prime }v^{\prime }{\it\theta}^{\prime }}$, towards the wall is enhanced in the buffer layer, but the transport of 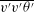$\overline{v^{\prime }v^{\prime }{\it\theta}^{\prime }}$ away from the wall is reduced in the outer layer for the rough case; similar behaviour is found for the vertical transport of turbulent momentum per unit mass, 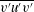$\overline{v^{\prime }u^{\prime }v^{\prime }}$. Above the roughness sublayer (3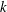$k$–5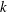$k$) it is found that most of the temperature field statistics, including higher-order moments and conditional averages, are highly similar for the smooth and rough surface flow, showing that the Townsend’s Reynolds number similarity hypothesis applies for the thermal field as well as the velocity field for the Reynolds number and 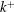$k^{+}$ considered in this study.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 787 , 25 January 2016 , pp. 84 - 115
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Araya, G. & Castillo, L. 2012 DNS of turbulent thermal boundary layers up to $re_{{\it\theta}}=2300$ . Intl J. Heat Mass Transfer 55 (15–16), 4003–4019.Google Scholar
Araya, G. & Castillo, L. 2013 Direct numerical simulations of turbulent thermal boundary layers subjected to adverse streamwise pressure gradients. Phys. Fluids 25 (9), 095107.Google Scholar
Araya, G., Castillo, L., Meneveau, C. & Jansen, K. 2011 A dynamic multi-scale approach for turbulent inflow boundary conditions in spatially developing flows. J. Fluid Mech. 670, 581–605.CrossRefGoogle Scholar
Araya, G., Jansen, K. & Castillo, L. 2009 Inlet condition generation for spatially developing turbulent boundary layers via multiscale similarity. J. Turbul.; p. N36. http://dx.doi.org/10.1080/14685240903329303.Google Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.Google Scholar
Belnap, B. J., van Rij, J. A. & Ligrani, P. M. 2002 A Reynolds analogy for real component surface roughness. Intl J. Heat Mass Transfer 45 (15), 3089–3099.Google Scholar
Blackwell, B.1972 The turbulent boundary layer on a porous plate: An experimental study of the heat transfer behavior with adverse pressure gradients. PhD thesis, Stanford University.Google Scholar
Brzek, B., Cal, R. B., Johansson, G. & Castillo, L. 2008 Transitionally rough zero pressure gradient turbulent boundary layers. Exp. Fluids 44 (1), 115–124.CrossRefGoogle Scholar
Cardillo, J., Chen, Y., Araya, G., Newman, J., Jansen, K. & Castillo, L. 2013 DNS of a turbulent boundary layer with surface roughness. J. Fluid Mech. 729, 603–637.Google Scholar
Choi, H. & Moin, P. 1994 Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys. 113 (1), 1–4.CrossRefGoogle Scholar
Dipprey, D. F. & Sabersky, R. H. 1963 Heat and momentum transfer in smooth and rough tubes at various Prandtl numbers. Intl J. Heat Mass Transfer 6 (5), 329–353.Google Scholar
Erm, L. P. & Joubert, P. N. 1991 Low-Reynolds-number turbulent boundary layers. J. Fluid Mech. 230, 1–44.Google Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsends Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17 (3), 035102.Google Scholar
Hoffmann, P. H. & Perry, A. E. 1979 The development of turbulent thermal layers on flat plates. Intl J. Heat Mass Transfer 22 (1), 39–46.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Jansen, K. E. 1999 A stabilized finite element method for computing turbulence. Comput. Methods Appl. Mech. Engng 174 (3–4), 299–317.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Kays, W. M. 1994 Turbulent Prandtl number – where are we? Trans. ASME J. Heat Transfer 116 (2), 284–295.Google Scholar
Kays, W. M. & Crawford, M. E. 1993 Convective Heat and Mass Transfer. McGraw-Hill.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kong, H., Choi, H. & Lee, J. S. 2000 Direct numerical simulation of turbulent thermal boundary layers. Phys. Fluids 12 (10), 2555–2568.Google Scholar
Li, Q., Schlatter, P., Brandt, L. & Henningson, D. S. 2009 DNS of a spatially developing turbulent boundary layer with passive scalar transport. Intl J. Heat Fluid Flow 30 (5), 916–929; The 3rd International Conference on Heat Transfer and Fluid Flow in Microscale.Google Scholar
Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140 (2), 233–258.CrossRefGoogle Scholar
Miyake, Y., Tsujimoto, K. & Nakaji, M. 2001 Direct numerical simulation of rough-wall heat transfer in a turbulent channel flow. Intl J. Heat Fluid Flow 22 (3), 237–244; Turbulent Heat and Mass Transfer - 3.CrossRefGoogle Scholar
Nagano, Y., Tsuji, T. & Houra, T. 1998 Structure of turbulent boundary layer subjected to adverse pressure gradient. Intl J. Heat Fluid Flow 19 (5), 563–572.Google Scholar
Nickels, T. B. 2010 IUTAM Symposium on The Physics of Wall-Bounded Turbulent Flows on Rough Walls. Springer.Google Scholar
Owen, P. R. & Thomson, W. R. 1963 Heat transfer across rough surfaces. J. Fluid Mech. 15, 321–334.Google Scholar
Pimenta, M. M., Moffat, R. J. & Kays, W. M.1975 The turbulent boundary layer: An experimental study of the transport of momentum and heat with the effect of roughness. Tech. Rep. HMT-21. Stanford University.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.Google Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Schultz, M. P. & Flack, K. A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to ${\it\delta}^{+}\approx 2000$ . Phys. Fluids 25 (10), 105102.Google Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. i. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228 (11), 4218–4231.Google Scholar
Stolz, S. & Adams, N. A. 2003 Large-eddy simulation of high-Reynolds-number supersonic boundary layers using the approximate deconvolution model and a rescaling and recycling technique. Phys. Fluids 15 (8), 2398–2412.Google Scholar
Sun, C.2008 Parallel algebraic multigrid for the pressure Poisson equation in a finite element Navier–Stokes solver. PhD thesis, Rensselaer Polytechnic Institute.Google Scholar
Teitel, M. & Antonia, R. A. 1993 Heat transfer in fully developed turbulent channel flow: comparison between experiment and direct numerical simulations. Intl J. Heat Mass Transfer 36 (6), 1701–1706.Google Scholar
Tennekes, H. & Lumley, J. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Wang, X. & Castillo, L. 2003 Asymptotic solutions in forced convection turbulent boundary layers. J. Turbul. 4, 006.Google Scholar
Wang, X., Castillo, L. & Araya, G. 2008 Temperature scalings and profiles in forced convection turbulent boundary layers. Trans. ASME J. Heat Transfer 130 (2), 021701 (17 pages).Google Scholar
Whiting, C. H. & Jansen, K. E. 2001 A stabilized finite element method for the incompressible Navier–Stokes equations using a hierarchical basis. Intl J. Numer. Meth. Fluids 35 (1), 93–116.Google Scholar
Whiting, C. H., Jansen, K. E. & Dey, S. 2003 Hierarchical basis for stabilized finite element methods for compressible flows. Comput. Meth. Appl. Mech. Engng 192 (47–48), 5167–5185.Google Scholar
Wu, X. & Moin, P. 2010 Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 22 (8), 085105.Google Scholar
Yaglom, A. M. & Kader, B. A. 1974 Heat and mass transfer between a rough wall and turbulent fluid flow at high Reynolds and Peclet numbers. J. Fluid Mech. 62, 601–623.Google Scholar