Article contents
Effect of interfacial viscosities on droplet migration at low surfactant concentrations
Published online by Cambridge University Press: 03 September 2020
Abstract
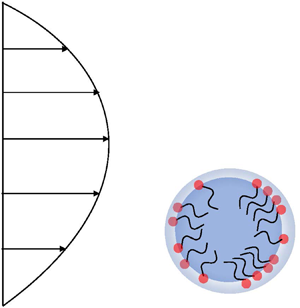
In this paper, we theoretically investigate the migration of a surfactant covered droplet in a Poiseuille flow by including the surface viscosities of the droplet. We employ a regular perturbation expansion for low surface Péclet numbers and solve the problem up to a second-order approximation. We represent the drop surface as a two-dimensional homogeneous fluid using the Bousinessq–Scriven law and employ Lamb's general solution to represent the velocity fields inside and outside the droplet. We obtain an expression for the cross-stream migration velocity of the droplet, where the surface viscosities are captured by the Bousinessq numbers for surface shear and surface dilatation. We elucidate the influence of the surface viscosities on the migration characteristics of the droplet and the surfactant redistribution on the droplet surface. Our study sheds light on the importance of including the droplet surface viscosities to accurately predict the migration characteristics of the droplet.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 9
- Cited by



