Article contents
Effect of inhaled air temperature on mucus dynamics in the proximal airways
Published online by Cambridge University Press: 03 January 2024
Abstract
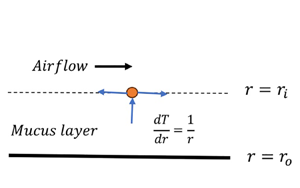
The aim of the present study is to understand the role of steam/cold-air inhalation on the mucus layer dynamics in the proximal airways. We model these flows as a viscoelastic liquid (lining the inner side of a tube) sheared by a turbulent airflow and subjected to a radial heat flow. The linear stability analysis of the resulting flow is carried out using numerical and thin-film approaches. The air–mucus interface tension, coupled with the azimuthal curvature, leads to the previously predicted axisymmetric capillary mode responsible for airway closure in distal airways. The viscoelasticity of the mucus leads to axisymmetric and new non-axisymmetric elastic modes, with the former possessing a higher growth rate. The axisymmetric elastic and capillary modes merge to give rise to a new ‘elasto-capillary mode’ possessing a growth rate nearly equal to the combined growth rate of the elastic and capillary modes. The analysis predicts a strong stabilising effect of the thermocapillarity induced by steam inhalation on the elasto-capillary mode. Thus steam decreases airway resistance, which could explain the observed therapeutic effect of steam inhalation. The opposite is the case when the inhaled air is colder than the body temperature, in agreement with the observations. The theoretical predictions are corroborated by the physical mechanism explaining the suppression/amplification of the elasto-capillary mode due to thermocapillarity.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 5
- Cited by



