Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T14:39:00.861Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of downstream turbulent region on the spiral vortex structures of a rotating-disk flow

Published online by Cambridge University Press:  04 April 2018

K. Lee Open the ORCID record for K. Lee [Opens in a new window] ,
Y. Nishio ,
S. Izawa  and
Y. Fukunishi
K. Lee*
Affiliation:
Department of Mechanical Systems Engineering, Tohoku University, Sendai 980-8579, Japan
Y. Nishio
Affiliation:
Department of Mechanical Systems Engineering, Tohoku University, Sendai 980-8579, Japan
S. Izawa
Affiliation:
Department of Mechanical Systems Engineering, Tohoku University, Sendai 980-8579, Japan
Y. Fukunishi
Affiliation:
Department of Mechanical Systems Engineering, Tohoku University, Sendai 980-8579, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations are carried out to investigate the role of the turbulent region in a self-sustaining system with a spiral vortex structure in the three-dimensional boundary layer over a rotating disk by solving the full Navier–Stokes equations. Two computational domains with two different azimuthal sizes, 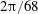$2\unicode[STIX]{x03C0}/68$ and 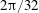$2\unicode[STIX]{x03C0}/32$, are used to deal with different initially dominant wavenumbers. An artificial disturbance is introduced by short-duration strong suction and blowing on the disk surface. After the flow field reaches a steady state, a turbulent region forms downstream of 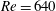$Re=640$. The turbulent region is then removed using two methods: a sponge region, and application of a slip condition at the wall. In both cases, the turbulent region disappears, leaving the spiral vortex structure upstream unaffected. The results suggest that the downstream turbulent region is not related to the velocity fluctuations that grow by the global instability. In addition, when the area where the slip condition is applied is changed from 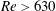$Re>630$ to 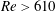$Re>610$, the velocity fluctuations decay. 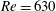The results indicate that the vibration source of the velocity fluctuations which grow by the global instability is located between $Re=611$ and $Re=630$.

JFM classification

Boundary Layers: Boundary layer stability Geophysical and Geological Flows: Rotating flows Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 274 - 296
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2015a Global linear instability of the rotating-disk flow investigated through simulations. J. Fluid Mech. 765, 612–631.10.1017/jfm.2015.2Google Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2015b Investigation of the global instability of the rotating-disk boundary layer. Proc. IUTAM 14, 321–328.10.1016/j.piutam.2015.03.054Google Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2016a Linear disturbances in the rotating-disk flow: a comparison between results from simulations, experiments and theory. Eur. J. Mech. (B/Fluids) 55, 170–181.10.1016/j.euromechflu.2015.09.010Google Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2016b On the global nonlinear instability of the rotating-disk flow over a finite domain. J. Fluid Mech. 803, 332–355.10.1017/jfm.2016.506Google Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2018 Transition to turbulence in the rotating-disk boundary-layer flow with stationary vortices. J. Fluid Mech. 836, 43–71.10.1017/jfm.2017.771Google Scholar
Balakumar, P. & Malik, M. 1990 Traveling disturbances in rotating-disk flow. Theor. Comput. Fluid Dyn. 2, 125–137.Google Scholar
Chebeci, T. & Stewartson, K. 1980 On stability and transition in three-dimensional flows. AIAA J. 18, 398–405.10.2514/3.50772Google Scholar
Davies, C. & Carpenter, P. W. 2003 Global behaviour corresponding to the absolute instability of the rotating-disk boundary layer. J. Fluid Mech. 486, 287–329.10.1017/S0022112003004701Google Scholar
Faller, A. J. 1991 Instability and transition of disturbed flow over a rotating disk. J. Fluid Mech. 230, 245–269.10.1017/S0022112091000782Google Scholar
Fedorov, B. I., Plavnik, G. Z. & Prokhorov, I. V. 1976 Transitional flow conditions on a rotating disk. J. Engng Phys. 31, 1448–1453.10.1007/BF00860579Google Scholar
Gregory, N., Stuart, J. T. & Walker, W. S. 1955 On the stability of three-dimensional boundary layers with application to the flow due to a rotating disk. Phil. Trans. R. Soc. Lond. A 248, 155–199.Google Scholar
Healey, J. J. 2010 Model for unstable global modes in the rotating-disk boundary layer. J. Fluid Mech. 663, 148–159.10.1017/S0022112010003836Google Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.10.1017/S0022112085003147Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2013 An experimental study of edge effects on rotating-disk transition. J. Fluid Mech. 716, 638–657.10.1017/jfm.2012.564Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2014 On the laminar–turbulent transition of the rotating-disk flow. J. Fluid Mech. 745, 132–163.10.1017/jfm.2014.80Google Scholar
Itoh, N. 2001a Structure of absolute instability in 3-D boundary layers. Part 1. Mathematical formulation. Trans. Japan. Soc. Aeronaut. Space Sci. 44, 96–100.10.2322/tjsass.44.96Google Scholar
Itoh, N. 2001b Structure of absolute instability in 3-D boundary layers. Part 2. Application to rotating-disk-flow. Trans. Japan. Soc. Aeronaut. Space Sci. 44, 101–105.10.2322/tjsass.44.101Google Scholar
Jarre, S., Gal, P. L. & Chauve, M. P. 1995 Experimental study of the rotating disk flow instability. Adv. Turbul. V 24, 246–250.10.1007/978-94-011-0457-9_44Google Scholar
von Kármán, T. 1921 Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1, 232–252.Google Scholar
Kawamura, T., Takami, H. & Kuwahara, K. 1986 Computation of high Reynolds number flow around a circular cylinder with surface roughness. Fluid Dyn. Res. 1, 145–162.10.1016/0169-5983(86)90014-6Google Scholar
Kobayashi, R., Kohama, Y. & Takamadate, T. 1980 Spiral vortices in boundary layer transition regime on a rotating disk. Acta Mech. 35, 71–82.10.1007/BF01190058Google Scholar
Kohama, Y. 1984 Study on boundary layer transition of a rotating disk. Acta Mech. 50, 193–199.10.1007/BF01170959Google Scholar
Lingwood, R. J. 1995 Absolute instability of the boundary layer on a rotating disk. J. Fluid Mech. 299, 17–22.10.1017/S0022112095003405Google Scholar
Lingwood, R. J. 1996 An experimental study of absolute instability of the rotating-disk boundary-layer flow. J. Fluid Mech. 314, 373–405.10.1017/S0022112096000365Google Scholar
Lingwood, R. J. 1997 Absolute instability of the Ekman layer and related rotating flows. J. Fluid Mech. 331, 405–428.10.1017/S0022112096004144Google Scholar
Malik, M. R., Wilkinson, S. P. & Orszag, S. A. 1981 Instability and transition in rotating disk flow. AIAA J. 19, 1131–1138.10.2514/3.7849Google Scholar
Miklavčič, M. & Wang, C. Y. 2004 The flow due to a rough rotating disk. Z. Angew. Math. Phys. 55, 235–246.10.1007/s00033-003-2096-6Google Scholar
Othman, H. & Corke, T. C. 2006 Experimental investigation of absolute instability of a rotating-disk boundary layer. J. Fluid Mech. 565, 63–94.10.1017/S0022112006001546Google Scholar
Pier, B. 2003 Finite-amplitude crossflow vortices, secondary instability and transition in the rotating-disk boundary layer. J. Fluid Mech. 487, 315–343.10.1017/S0022112003004981Google Scholar
Pier, B. 2007 Primary cross flow vortices, secondary absolute instabilities and their control in the rotating-disk boundary layer. J. Engng Maths 57, 237–251.10.1007/s10665-006-9095-5Google Scholar
Pier, B. 2013 Transition near the edge of a rotating disk. J. Fluid Mech. 737, R1.10.1017/jfm.2013.578Google Scholar
Pier, B. & Huerre, P. 2001 Nonlinear self-sustained structures and fronts in spatially developing wake flows. J. Fluid Mech. 435, 145–174.10.1017/S0022112001003652Google Scholar
Pier, B., Huerre, P., Chomaz, J.-M. & Couairon, A. 1998 Steep nonlinear global modes in spatially developing media. Phys. Fluids 10 (10), 2433–2435.10.1063/1.869784Google Scholar
Smith, N. H.1947 Exploratory investigation of laminar-boundary-layer oscillations on a rotating disk. NACA TN 1227.Google Scholar
Viaud, B., Serre, E. & Chomaz, J.-M. 2008 The elephant mode between two rotating disks. J. Fluid Mech. 598, 451–464.10.1017/S0022112007009962Google Scholar
Viaud, B., Serre, E. & Chomaz, J.-M. 2011 Transition to turbulence through steep global-modes cascade in an open rotating cavity. J. Fluid Mech. 688, 493–506.10.1017/jfm.2011.393Google Scholar
Wilkinson, S. P. & Malik, M. R. 1983 Stability experiments in rotating-disk flow. In AIAA 16th Fluid and Plasma Dynamics Conference. American Institute of Aeronautics and Astronautics.Google Scholar