Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Yanan
Thompson, David
and
Hu, Zhiwei
2020.
Numerical investigations on the flow over cuboids with different aspect ratios and the emitted noise.
Physics of Fluids,
Vol. 32,
Issue. 2,
Woyciekoski, Marcos L.
Endres, Luiz Augusto M.
de Paula, Alexandre V.
and
Möller, Sergio V.
2020.
Influence of the free end flow on the bistability phenomenon after two side by side finite height cylinders with aspect ratios of 3 and 4 and high blockage.
Ocean Engineering,
Vol. 195,
Issue. ,
p.
106658.
Bhamitipadi Suresh, Dhanush
Aju, Emmanuvel Joseph
and
Jin, Yaqing
2020.
Turbulent boundary layer flow over two side-by-side wall-mounted cylinders: Wake characteristics and aerodynamic loads.
Physics of Fluids,
Vol. 32,
Issue. 11,
Aboueian, J.
Sohankar, A.
Rastan, M.R.
and
Ghodrat, M.
2021.
An experimental study on flow over two finite wall-mounted square cylinders in a staggered arrangement.
Ocean Engineering,
Vol. 240,
Issue. ,
p.
109954.
Essel, Ebenezer E.
Tachie, Mark F.
and
Balachandar, Ram
2021.
Time-resolved wake dynamics of finite wall-mounted circular cylinders submerged in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Freidooni, F.
Sohankar, A.
Rastan, M.R.
and
Shirani, E.
2021.
Flow field around two tandem non-identical-height square buildings via LES.
Building and Environment,
Vol. 201,
Issue. ,
p.
107985.
Bhamitipadi Suresh, Dhanush
Aju, Emmanuvel Joseph
Pham, Dat Thanh
and
Jin, Yaqing
2021.
On the incipient sediment suspension downstream of three-dimensional wall-mounted obstacles.
Physics of Fluids,
Vol. 33,
Issue. 8,
Rastan, M.R.
Shahbazi, H.
Sohankar, A.
Alam, Md. Mahbub
and
Zhou, Yu
2021.
The wake of a wall-mounted rectangular cylinder: Cross-sectional aspect ratio effect.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 213,
Issue. ,
p.
104615.
Heng, H.
and
Sumner, D.
2022.
The mean pressure distribution on the free end of a square prism.
International Journal of Heat and Fluid Flow,
Vol. 96,
Issue. ,
p.
109005.
Li, Ming
Li, Qiusheng
Shi, Hao-Yun
and
Li, Ming-Shui
2022.
Large-Scale Gust Effect on Aerodynamic Pressures and Forces on a Square Cylinder.
SSRN Electronic Journal ,
Jiang, Chaoyang
de Silva, Charitha
Doolan, Con J.
and
Moreau, Danielle
2022.
The Effect of Pressure Gradient on the Aeroacoustics and Wake Dynamics of a Finite Wall-Mounted Square Cylinder.
Crane, R.J.
Popinhak, A.R.
Martinuzzi, R.J.
and
Morton, C.
2022.
Tomographic PIV investigation of vortex shedding topology for a cantilevered circular cylinder.
Journal of Fluid Mechanics,
Vol. 931,
Issue. ,
Chen, Guang
Li, Xiao-Bai
Sun, Bo
and
Liang, Xi-Feng
2022.
Effect of incoming boundary layer thickness on the flow dynamics of a square finite wall-mounted cylinder.
Physics of Fluids,
Vol. 34,
Issue. 1,
da Silva, Barbara L.
Hahn, Dylan G. H.
Sumner, David
and
Bergstrom, Donald J.
2022.
Mean wake and aerodynamic forces for surface-mounted finite-height square prisms of very small aspect ratio.
Physics of Fluids,
Vol. 34,
Issue. 11,
Zargar, Arash
Goswami, Shubham
and
Hemmati, Arman
2022.
On the wake of a large depth ratio wall-mounted prism at a normal incident angle.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 230,
Issue. ,
p.
105168.
Li, Jiawei
Rinoshika, Hiroka
Han, Xiaolei
and
Rinoshika, Akira
2022.
Effect of a front inclined hole on multiscale vortical structures around a wall-mounted cube.
Physics of Fluids,
Vol. 34,
Issue. 7,
Mohammadi, Ali
Morton, Chris
and
Martinuzzi, Robert J.
2022.
Effect of boundary layer state on the wake of a cantilevered square cylinder of aspect ratio 4.
Physical Review Fluids,
Vol. 7,
Issue. 8,
Goswami, Shubham
and
Hemmati, Arman
2022.
Mechanisms of wake asymmetry and secondary structures behind low aspect-ratio wall-mounted prisms.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Hu, Xiao
and
Morgans, Aimee S.
2022.
Attenuation of the unsteady loading on a high-rise building using feedback control.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Cao, Yong
Tamura, Tetsuro
Zhou, Dai
Bao, Yan
and
Han, Zhaolong
2022.
Topological description of near-wall flows around a surface-mounted square cylinder at high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
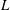 $L$ to width
$L$ to width 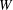 $W$) investigated in the experiments were
$W$) investigated in the experiments were 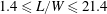 $1.4\leqslant L/W\leqslant 21.4$ and the oncoming boundary-layer thicknesses were
$1.4\leqslant L/W\leqslant 21.4$ and the oncoming boundary-layer thicknesses were 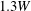 $1.3W$ and
$1.3W$ and 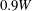 $0.9W$ at a Reynolds number based on cylinder width of
$0.9W$ at a Reynolds number based on cylinder width of 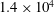 $1.4\times 10^{4}$ and
$1.4\times 10^{4}$ and 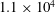 $1.1\times 10^{4}$, respectively. In complementary simulations, the cylinder aspect ratios investigated were 1.4, 4.3, 10 and 18.6. The cylinder wake structure was visualised in three-dimensional space using a vortex core detection method and decomposed to its oscillation modes using the spectral proper orthogonal decomposition (SPOD) technique. A parametric diagram is proposed to predict whether the time-averaged wake structure is a dipole or a quadrupole pattern, based on oncoming boundary-layer height and aspect ratio. Cellular shedding occurs when the aspect ratio is high with up to three shedding cells occurring across the span for aspect ratios
$1.1\times 10^{4}$, respectively. In complementary simulations, the cylinder aspect ratios investigated were 1.4, 4.3, 10 and 18.6. The cylinder wake structure was visualised in three-dimensional space using a vortex core detection method and decomposed to its oscillation modes using the spectral proper orthogonal decomposition (SPOD) technique. A parametric diagram is proposed to predict whether the time-averaged wake structure is a dipole or a quadrupole pattern, based on oncoming boundary-layer height and aspect ratio. Cellular shedding occurs when the aspect ratio is high with up to three shedding cells occurring across the span for aspect ratios 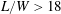 $L/W>18$. Each of these cells sheds at a distinct frequency, as evidenced by the spectral content of the surface pressure measured on the side face and the near-wake velocity. Amplitude modulation is also observed in the vortex shedding, which explains the amplitude modulation of the acoustic pressure emitted by square FWMCs. SPOD is shown to be a viable method to identify the occurrence of cellular shedding in the wake.
$L/W>18$. Each of these cells sheds at a distinct frequency, as evidenced by the spectral content of the surface pressure measured on the side face and the near-wake velocity. Amplitude modulation is also observed in the vortex shedding, which explains the amplitude modulation of the acoustic pressure emitted by square FWMCs. SPOD is shown to be a viable method to identify the occurrence of cellular shedding in the wake.

