Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T11:36:13.778Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of an internal nonlinear rotational dissipative element on vortex shedding and vortex-induced vibration of a sprung circular cylinder

Published online by Cambridge University Press:  31 August 2017

Ravi Kumar R. Tumkur Open the ORCID record for Ravi Kumar R. Tumkur [Opens in a new window] ,
Arne J. Pearlstein ,
Arif Masud ,
Oleg V. Gendelman ,
Antoine B. Blanchard ,
Lawrence A. Bergman  and
Alexander F. Vakakis
Ravi Kumar R. Tumkur*
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, IL 61801, USA
Arne J. Pearlstein
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, IL 61801, USA
Arif Masud
Affiliation:
Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, IL 61801, USA
Oleg V. Gendelman
Affiliation:
Faculty of Mechanical Engineering, Technion-Israel Institute of Technology, Haifa 3200003, Israel
Antoine B. Blanchard
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, IL 61801, USA
Lawrence A. Bergman
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, IL 61801, USA
Alexander F. Vakakis
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We computationally investigate coupling of a nonlinear rotational dissipative element to a sprung circular cylinder allowed to undergo transverse vortex-induced vibration (VIV) in an incompressible flow. The dissipative element is a ‘nonlinear energy sink’ (NES), consisting of a mass rotating at fixed radius about the cylinder axis and a linear viscous damper that dissipates energy from the motion of the rotating mass. 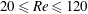We consider the Reynolds number range $20\leqslant Re\leqslant 120$, with 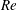$Re$ based on cylinder diameter and free-stream velocity, and the cylinder restricted to rectilinear motion transverse to the mean flow. Interaction of this NES with the flow is mediated by the cylinder, whose rectilinear motion is mechanically linked to rotational motion of the NES mass through nonlinear inertial coupling. The rotational NES provides significant ‘passive’ suppression of VIV. Beyond suppression however, the rotational NES gives rise to a range of qualitatively new behaviours not found in transverse VIV of a sprung cylinder without an NES, or one with a ‘rectilinear NES’, considered previously. Specifically, the NES can either stabilize or destabilize the steady, symmetric, motionless-cylinder solution and can induce conditions under which suppression of VIV (and concomitant reduction in lift and drag) is accompanied by a greatly elongated region of attached vorticity in the wake, as well as conditions in which the cylinder motion and flow are temporally chaotic at relatively low 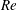$Re$.

JFM classification

Nonlinear Dynamical Systems: Chaos Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 196 - 235
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anagnostopoulos, P. 2000a Numerical study of the flow past a cylinder excited transversely to the incident stream. Part 1. Lock-in zone, hydrodynamic forces and wake geometry. J. Fluids Struct. 14, 819–851.CrossRefGoogle Scholar
Anagnostopoulos, P. 2000b Numerical study of the flow past a cylinder excited transversely to the incident stream. Part 2. Timing of vortex shedding, aperiodic phenomena and wake parameters. J. Fluids Struct. 14, 853–882.Google Scholar
Anagnostopoulos, P. & Bearman, P. W. 1992 Response characteristics of a vortex-excited cylinder at low Reynolds numbers. J. Fluids Struct. 6, 39–50.Google Scholar
Argoul, P. & Le, T.-P. 2003 Instantaneous indicators of structural behaviour based on the continuous cauchy wavelet analysis. Mech. Sys. Sign. Proc. 17, 243–250.Google Scholar
Arnol’d, V. I. 1988 Dynamical Systems III, Encyclopaedia of Mathematical Sciences. Springer.Google Scholar
Baek, S.-J. & Sung, H. J. 2000 Quasi-periodicity in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 408, 275–300.CrossRefGoogle Scholar
Batcho, P. & Karniadakis, G. E. 1991 Chaotic transport in two- and three-dimensional flow past a cylinder. Phys. Fluids A 3, 1051–1062.CrossRefGoogle Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.Google Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27, 648–658.Google Scholar
Blackburn, H. & Henderson, R. 1996 Lock-in behavior in simulated vortex-induced vibration. Exp. Therm. Fluid Sci. 12, 184–189.Google Scholar
Calderer, R. & Masud, A. 2010 A multiscale stabilized ALE formulation for incompressible flows with moving boundaries. Comput. Mech. 46, 185–197.Google Scholar
Chung, J. & Hulbert, G. M. 1993 A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-𝛼 method. Trans. ASME J. Appl. Mech. 60, 371–375.CrossRefGoogle Scholar
Cossu, C. & Morino, L. 2000 On the instability of a spring-mounted circular cylinder in a viscous flow at low Reynolds numbers. J. Fluids Struct. 14, 183–196.Google Scholar
Dauchy, C., Dus̆sek, J. & Fraunié, P. 1997 Primary and secondary instabilities in the wake of a cylinder with free ends. J. Fluid Mech. 332, 295–339.Google Scholar
Deshmukh, S. R. & Vlachos, D. G. 2005 Novel micromixers driven by flow instabilities: application to post-reactors. AIChE J. 51, 3193–3204.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 nek5000 Web page. http://nek5000.mcs.anl.gov.Google Scholar
Gabbai, R. D. & Benaroya, H. 2005 An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 282, 575–616.Google Scholar
Gendelman, O. V. 2011 Targeted energy transfer in systems with external and self-excitation. Proc. Inst. Mech. Engrs C 225, 2007–2043.Google Scholar
Gendelman, O. V., Sigalov, G., Manevitch, L. I., Mane, M., Vakakis, A. F. & Bergman, L. A. 2012 Dynamics of an eccentric rotational nonlinear energy sink. J. Appl. Mech. Trans. ASME 79, 011012-9.CrossRefGoogle Scholar
Grassberger, P. & Procaccia, I. 1983 Characterization of strange attractors. Phys. Rev. Lett. 50, 346–349.Google Scholar
Grossmann, A. & Morlet, J. 1984 Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 15, 723–736.Google Scholar
Harris, F. J. 1978 On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 66, 51–83.Google Scholar
Hegger, R., Kantz, H. & Schreiber, T. 1999 Practical implementation of nonlinear time series methods: the TISEAN package. Chaos 9, 413–435.Google Scholar
Henderson, R. D. 1995 Details of the drag curve near the onset of vortex shedding. Phys. Fluids 7, 2102–2104.Google Scholar
Jansen, K. E., Whiting, C. H. & Hulbert, G. M. 2000 A generalized-𝛼 method for integrating the filtered Navier–Stokes equations with a stabilized finite element method. Comput. Meth. Appl. Mech. Engng 190, 305–319.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1989 The crisis of transport measures in chaotic flow past a cylinder. Phys. Fluids A 1, 628–630.CrossRefGoogle Scholar
Lee, J. H. & Bernitsas, M. M. 2011 High-damping, high-Reynolds VIV tests for energy harnessing using the VIVACE converter. Ocean Engng 38, 1697–1712.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2006 The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 22, 857–864.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.Google Scholar
Li, J., Sun, J. & Roux, B. 1992 Numerical study of an oscillating cylinder in uniform flow and in the wake of an upstream cylinder. J. Fluid Mech. 237, 457–478.Google Scholar
Mittal, S. & Singh, S. 2005 Vortex-induced vibrations at subcritical Re . J. Fluid Mech. 534, 185–194.Google Scholar
Nakano, M. & Rockwell, D. 1994 Flow structure in the frequency-modulated wake of a cylinder. J. Fluid Mech. 266, 93–119.Google Scholar
Olinger, D. J. 1993 A low-dimensional model for chaos in open fluid flows. Phys. Fluids A 5, 1947–1951.Google Scholar
Olinger, D. J. & Sreenivasan, K. R. 1988 Nonlinear dynamics of the wake of an oscillating cylinder. Phys. Rev. Lett. 60, 797–800.Google Scholar
Païdoussis, M. P., Price, S. J. & de Langre, E. 2011 Fluid-Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Prasanth, T. K. & Mittal, S. 2009 Vortex-induced vibration of two circular cylinders at low Reynolds number. J. Fluids Struct. 25, 731–741.Google Scholar
Pulliam, T. H. & Vastano, J. A. 1993 Transition to chaos in an open unforced 2D flow. J. Comput. Phys. 105, 133–149.Google Scholar
Roshko, A.1954 On the drag and shedding frequency of two-dimensional bluff bodies. National Advisory Committee for Aeronautics, TN 3169.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19, 389–447.Google Scholar
Shiels, D., Leonard, A. & Roshko, A. 2001 Flow-induced vibration of a circular cylinder at limiting structural parameters. J. Fluids Struct. 15, 3–21.Google Scholar
Sreenivasan, K. R. 1985 Transition and turbulence in fluid flows and low-dimensional chaos. In Frontiers in Fluid Mechanics (ed. Davis, S. H. & Lumley, J. L.), pp. 41–67. Springer.Google Scholar
Tumkur, R. K. R., Calderer, R., Masud, A., Pearlstein, A. J., Bergman, L. A. & Vakakis, A. F. 2013 Computational study of vortex-induced vibration of a sprung rigid circular cylinder with a strongly nonlinear internal attachment. J. Fluids Struct. 40, 214–232.Google Scholar
Tumkur, R. K. R., Fischer, P. F., Bergman, L. A., Vakakis, A. F. & Pearlstein, A. J. 2017 Stability of the steady, two-dimensional flow past a linearly-sprung circular cylinder. J. Fluid Mech. (submitted).Google Scholar
Vakakis, A. F., Gendelman, O. V., Bergman, L. A., McFarland, D. M., Kerschen, G. & Lee, Y. S. 2008 Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems, Vol. I and II. Springer.Google Scholar
Van Atta, C. W. & Gharib, M. 1987 Ordered and chaotic vortex streets behind circular cylinders at low Reynolds numbers. J. Fluid Mech. 174, 113–133.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.Google Scholar
Zielinska, B. J. A. & Wesfreid, J. E. 1995 On the spatial structure of global modes in wake flow. Phys. Fluids 7, 1418–1424.Google Scholar
Supplementary material: File

Download undefined(File)
File 226.2 KB
Supplementary material: PDF

Kumar et al. supplementary materal

Supplementary Material

Download Kumar et al. supplementary materal(PDF)
PDF 228.7 KB