Article contents
The effect of a uniform through-surface flow on a cylinder and sphere
Published online by Cambridge University Press: 23 March 2016
Abstract
The effect of a uniform through-surface flow (velocity 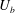 $U_{b}$) on a rigid and stationary cylinder and sphere (radius
$U_{b}$) on a rigid and stationary cylinder and sphere (radius  $a$) fixed in a free stream (velocity
$a$) fixed in a free stream (velocity 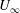 $U_{\infty }$) is analysed analytically and numerically. The flow is characterised by a dimensionless blow velocity
$U_{\infty }$) is analysed analytically and numerically. The flow is characterised by a dimensionless blow velocity 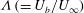 ${\it\Lambda}\,(=U_{b}/U_{\infty })$ and Reynolds number
${\it\Lambda}\,(=U_{b}/U_{\infty })$ and Reynolds number 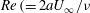 $Re\,(=2aU_{\infty }/{\it\nu}$, where
$Re\,(=2aU_{\infty }/{\it\nu}$, where  ${\it\nu}$ is the kinematic viscosity). High resolution numerical calculations are compared against theoretical predictions over the range
${\it\nu}$ is the kinematic viscosity). High resolution numerical calculations are compared against theoretical predictions over the range 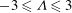 $-3\leqslant {\it\Lambda}\leqslant 3$ and
$-3\leqslant {\it\Lambda}\leqslant 3$ and 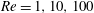 $Re=1,10,100$ for planar flow past a cylinder and axisymmetric flow past a sphere. For
$Re=1,10,100$ for planar flow past a cylinder and axisymmetric flow past a sphere. For 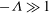 $-{\it\Lambda}\gg 1$, the flow is viscously dominated in a thin boundary layer of thickness
$-{\it\Lambda}\gg 1$, the flow is viscously dominated in a thin boundary layer of thickness 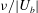 ${\it\nu}/|U_{b}|$ adjacent to the rigid surface which develops in a time
${\it\nu}/|U_{b}|$ adjacent to the rigid surface which develops in a time 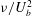 ${\it\nu}/U_{b}^{2}$; the surface vorticity scales as
${\it\nu}/U_{b}^{2}$; the surface vorticity scales as 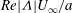 $Re|{\it\Lambda}|U_{\infty }/a$ for a cylinder and sphere. A boundary layer analysis is developed to analyse the unsteady viscous forces. Numerical results show that the surface pressure and vorticity distribution within the boundary layer agrees with a steady state analysis. The flow downstream of the body is irrotational so the wake volume flux,
$Re|{\it\Lambda}|U_{\infty }/a$ for a cylinder and sphere. A boundary layer analysis is developed to analyse the unsteady viscous forces. Numerical results show that the surface pressure and vorticity distribution within the boundary layer agrees with a steady state analysis. The flow downstream of the body is irrotational so the wake volume flux, 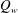 $Q_{w}$, is zero and the drag force is
$Q_{w}$, is zero and the drag force is 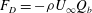 $F_{D}=-{\it\rho}U_{\infty }Q_{b}$, where
$F_{D}=-{\it\rho}U_{\infty }Q_{b}$, where 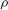 ${\it\rho}$ is the density of the fluid and
${\it\rho}$ is the density of the fluid and 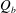 $Q_{b}$ is the normal flux through the body surface. The drag coefficient is therefore
$Q_{b}$ is the normal flux through the body surface. The drag coefficient is therefore 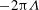 $-2{\rm\pi}{\it\Lambda}$ or
$-2{\rm\pi}{\it\Lambda}$ or 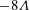 $-8{\it\Lambda}$ for a cylinder or sphere, respectively. A dissipation argument is applied to analyse the drag force; the rate of working of the drag force is balanced by viscous dissipation, flux of stagnation pressure and rate of work by viscous stresses due to sucking. At large
$-8{\it\Lambda}$ for a cylinder or sphere, respectively. A dissipation argument is applied to analyse the drag force; the rate of working of the drag force is balanced by viscous dissipation, flux of stagnation pressure and rate of work by viscous stresses due to sucking. At large 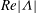 $Re|{\it\Lambda}|$, the drag force is largely determined by viscous dissipation for a cylinder, with a weak contribution by the normal viscous stresses, while for a sphere, only
$Re|{\it\Lambda}|$, the drag force is largely determined by viscous dissipation for a cylinder, with a weak contribution by the normal viscous stresses, while for a sphere, only 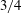 $3/4$ of the drag force is determined by viscous dissipation with the remaining
$3/4$ of the drag force is determined by viscous dissipation with the remaining 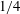 $1/4$ due to the flux of stagnation pressure through the sphere surface. When
$1/4$ due to the flux of stagnation pressure through the sphere surface. When 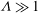 ${\it\Lambda}\gg 1$, the boundary layer thickness initially grows linearly with time as vorticity is blown away from the rigid surface. The vorticity in the boundary layer is weakly dependent on viscous effects and scales as
${\it\Lambda}\gg 1$, the boundary layer thickness initially grows linearly with time as vorticity is blown away from the rigid surface. The vorticity in the boundary layer is weakly dependent on viscous effects and scales as 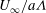 $U_{\infty }/a{\it\Lambda}$ or
$U_{\infty }/a{\it\Lambda}$ or 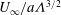 $U_{\infty }/a{\it\Lambda}^{3/2}$ for a cylinder and sphere, respectively. For large blow velocity, the vorticity is swept into two well-separated shear layers and the maximum vorticity decreases due to diffusion. The drag force is related to the vorticity distribution on the body surface and an approximate expression can be derived by considering the first term of a Fourier expansion in the surface vorticity. It is found that the drag coefficient
$U_{\infty }/a{\it\Lambda}^{3/2}$ for a cylinder and sphere, respectively. For large blow velocity, the vorticity is swept into two well-separated shear layers and the maximum vorticity decreases due to diffusion. The drag force is related to the vorticity distribution on the body surface and an approximate expression can be derived by considering the first term of a Fourier expansion in the surface vorticity. It is found that the drag coefficient 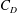 $C_{D}$ for a cylinder (corrected for flow boundedness) is weakly dependent on
$C_{D}$ for a cylinder (corrected for flow boundedness) is weakly dependent on 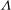 ${\it\Lambda}$ while for a sphere,
${\it\Lambda}$ while for a sphere, 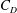 $C_{D}$ decreases with
$C_{D}$ decreases with 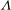 ${\it\Lambda}$.
${\it\Lambda}$.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 6
- Cited by



